带负顾客的非空竭服务休假排队模型非负解的存在唯一性

阿力木·米吉提

(新疆广播电视大学，新疆乌鲁木齐830049)

0 引言

E.Glenbe于1989年首次提出了带有负顾客(负神经元)的新型神经网络系统［1］，之后他又把负顾客引进了排队模型和排队网络中［2-3］.E.Glenbe在研究排队系统时，把到达系统的顾客分成2种:一种是正(普通)顾客，他们到达系统后接受系统提供的正常服务;另一种是负顾客，负顾客是一种新型的顾客，其本身不需要系统提供任何服务，他们到达后，若系统是空闲的，则立刻从系统中消失;若系统内有接受服务的正顾客，则立即把他带走.负顾客概念的提出，使许多交通、机械、控制和计算机等领域中的现实问题找到了解决方法，引起了国内外学者的广泛关注，从而对负顾客排队进行了一系列的研究［4-12］.文献［10］将负顾客引进非空竭服务休假且正顾客有流失的M/G/1排队系统，利用求吸收分布以及普通M/G/1排队系统的稳态条件，研究了一类带有负顾客且正顾客有流失的M/G/1非空竭服务休假排队系统的稳态条件.本文运用C0-半群理论研究此系统的时间依赖解，证明此系统正时间依赖解的存在唯一性.

1 系统模型及模型的转换

文献［10］把带有负顾客的非空竭服务休假排队系统的数学模型用以下方程组描述:

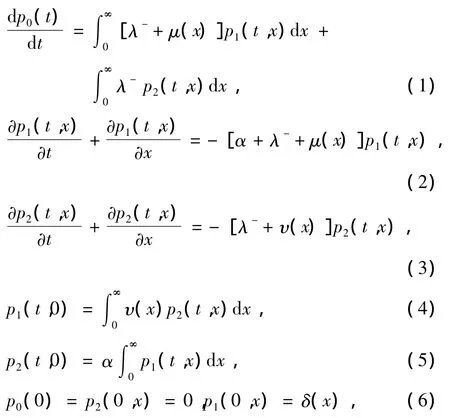
其中(t，x)∈［0，∞)×［0，∞)，p0(t)表示在时刻 t顾客已结束服务离开系统的概率，p1(t，x)dx表示在时刻t服务器正在为顾客服务，并服务已逝去的时间在［x，x+dx)之间的概率，p2(t，x)dx表示在时刻t服务器处于工作休假期，并休假已用去的时间在［x，x+dx)之间的概率.λ-表示负顾客到达系统的概率，α表示正常状态率，μ(x)表示服务失效率，υ(x)表示休假失效率.

选取状态空间为

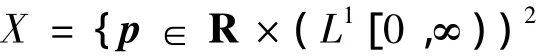
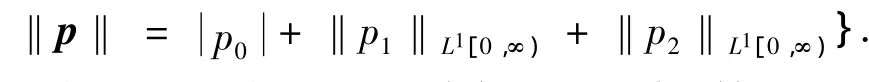
显然X是1个Banach空间.下面引进算子及其定义域.

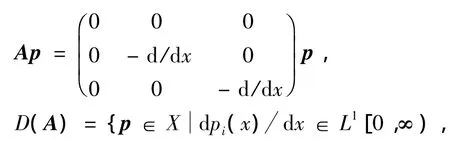
pi(x)(i=1，2)是绝对连续函数}，

D(U)=D(E)=X.

这里p=(p0，p1(x)，p2(x))'，则方程组(1)～(6)可以描述为Banach空间 X上的1个抽象Cauchy问题:

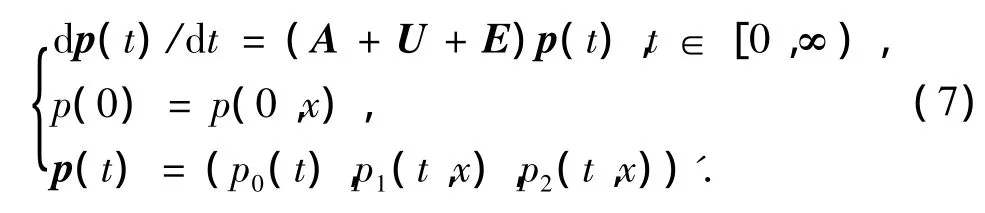
2 系统(7)非负解的存在唯一性

证分4步证明此定理.第1步估计A的豫解式.第2步验证D(A)在X中的稠密性.第3步证明U和E为有界线性算子，进而推出A+U+E生成1个C0-半群T(t).最后由算子的耗散性和Philips定理得到T(t)是1个正压缩C0-半群.

对给定的 y∈X，考虑方程(γI-A)p=y，即

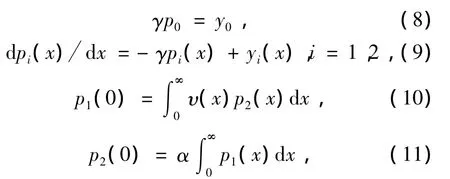
解方程(8)和(9)得到

由(10)～(13)式与Fubini定理有(不妨设γ＞α+υ)

将(15)式代入(14)式得

这里

用Fubini定理推出

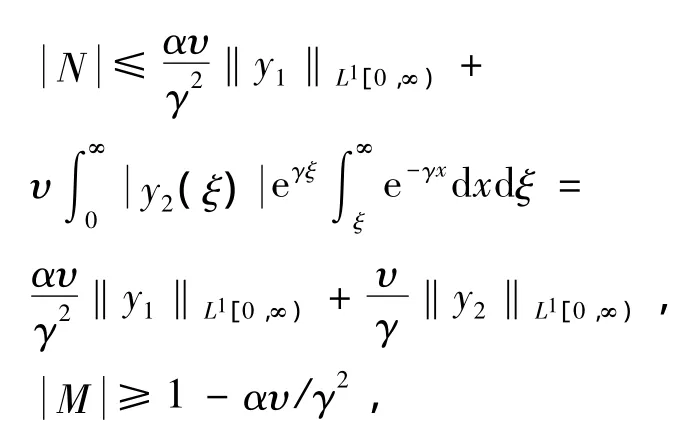
从而有

结合(15)式与(16)式得到

由(12)～(17)式与Fubini定理有

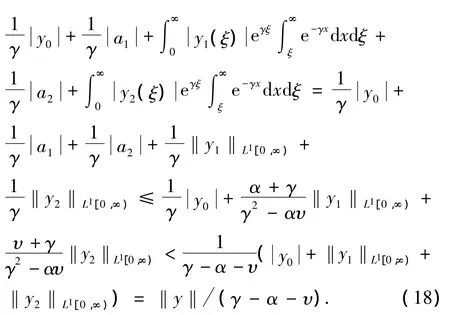
当γ＞α+υ时，(18)式中用了不等式

(18)式表明，当 γ ＞α+υ时，(γI-A)-1存在且(γI-A)-1∶X→ D(A)，满足 ‖(γI-A)-1‖≤1/(γ-α-υ).

由文献［13］知L在X中稠密.于是只需证明D(A)在L中稠密即可.

任取 p=(p0，p1(x)，p2(x))∈ L，则存在常数ci＞0，使得 ∀x∈［0，ci］，有 pi(x)=0(i=1，2).所以，当 x∈［0，s］时，有 pi(x)=0，其中 0＜ s＜min{c1，c2}.定义

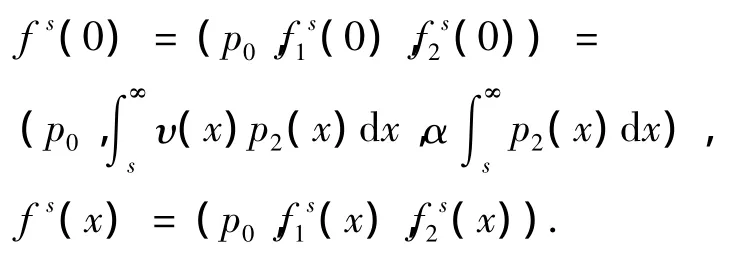
这里

则不难验证 fs∈D(A).此外，当s→0时，

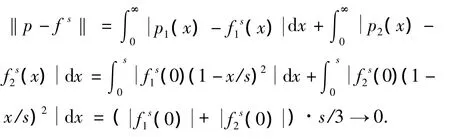
这说明D(A)在L中稠密，即D(A)在X中稠密.由上面的2步与Hille-Yosida定理［14］推出A生成1个C0-半群.

第3步证明U和E是有界线性算子.∀p(x)=(p0，p1(x)，p2(x))∈ X 有

以上2式说明U和E是有界算子.由定义容易验证它们是线性算子.结合 C0-半群的扰动理论［14］知A+U+E生成1个C0-半群T(t).

第4步证明A+U+E是dispersive算子.

对 p(x)=(p0，p1(x)，p2(x))∈ D(A)，令

其中

如果定义Vi={x∈［0，∞)和，则有

对p∈D(A)与上述的φ(x)，由(19)式与边界条件推出

此式说明算子A+U+E是dispersive.结合第1步、第2步、第4步和Philips定理得到A+U+E生成1个正压缩C0-半群.再由半群的唯一性理论即知，这个正定压缩C0-半群就是 T(t).定理1证毕.

类似于定理1的推导过程，易得下面结果.

推论1A+U生成1个正定压缩C0-半群Q(t).

根据定理1和文献［15］得到本文主要结果.

证由定理1与文献［15］易知系统存在唯一的正时间依赖解p(t，x)并把它可以表示为

此式与定理1结合推出

另一方面，pi(t，x)(i=1，2)满足(1)～(6)式，故有

因此‖p(t，·)‖=‖p(0)‖=1.定理2 证毕.

［1］Gelenbe E.Random neural networks with negative and positive signals and product form solution ［J］.Neural Comput，1989，1(4):502-510.

［2］Gelenbe E，Glynn P，Sigman K.Queues with negative arrivals［J］.JAppl Prob，1991，28(1):245-250.

［3］Gelenbe E.Product form networks with negative and positive customers［J］.JAppl Prob，1991，28(3):656-663.

［4］Harrison P G，Pitel E.The M/G/1 queue with negative customers［J］.AdvAppl Prob，1996，28(2):540-566.

［5］ Harrison P G，Pitel E.Sojourn times in single-server queues with negative customers［J］.JAppl Prob，1993，30(4):943-963.

［6］周文慧，邓永录.具有负顾客到达的M/G/1可修排队系统［J］.运筹学学报，2006，10(2):28-36.

［7］伍慧玲，尹小玲.有单移除策略的M/G/1重试可修排队系统 ［J］.中山大学学报:自然科学版，2005，44(S1):133-137.

［8］尹小玲，邓永录，招雁鸿.带有负顾客且正顾客有流失的M/G/1休假排队系统［C］∥中国运筹学会可靠性学会第7届学术会议论文集.北京:清华大学出版社，2005:123-128.

［9］唐学德，朱翼隽，冯艳刚.具有2种服务的负顾客Mε/(G1/G2)/1排队系统［J］.江西师范大学学报:自然科学版，2007，31(5):500-503.

［10］尹小玲.带负顾客的非空竭服务休假排队系统的稳态分析［J］.中山大学学报:自然科学版，2008，47(2):1-4.

［11］刘再明，吴锦标.具有负顾客和抢占反馈的M/G/1随机休假排队系统［J］.应用数学，2010，23(2):244-251.

［12］高显彩，单雪红，朱翼隽.带负顾客，反馈，服务台可修的M/G/1重试排队系统［J］.应用数学学报，2012，35(5):935-943.

［13］Adams RA.Sobolev space［M］.New York:Academic Press，1975.

［14］Gupur G，Li Xuezhi，Zhu Guangtian.Functional analysismethod in queueing theory［M］.Hertfordshire:ResearchInformation Ltd，2001.

［15］Engel K J，Nagel R.One-parameter semigroups for linear evolution equations［M］.New York:Springer-Verlag，2000.