具有饱和接种率的传染病模型的稳定性

王爱丽

(宝鸡文理学院数学系，陕西 宝鸡 721013)

0 引言

预防接种是人类抵御传染病侵袭最重要、最有效的措施，也是一个国家和地区科学技术发展和公共卫生形象的具体体现.目前我国已成为世界上最广泛使用疫苗的国家之一.我国免疫规划全面展开，已扩大到14种疫苗，可预防包括狂犬病、黄热病、小儿麻痹症、乙肝等传染病在内的15种疾病.因此，设计一种有效地接种疫苗的策略以控制传染病的爆发、减小传染病爆发时的影响以及降低接种疫苗的成本已成为医务人员和科研工作者关注的热点问题之一［1-8］.常用的接种策略有 2种，即连续的接种［9-10］和脉冲式的接种［11-15］，但是这些策略都没有考虑医疗资源的有限性.根据卫生部的报道，2009年当甲型H1N1流感爆发时，由于没有足够的疫苗，在不同的省份以及不同年龄阶段的人群，接种策略均不同.

经典的传染病模型总是假定接种比例与易感者的数量成正比，这要求一个国家或地区所能提供的疫苗数量非常大，因此，它是不合理的.实际上，每个国家或地区所存储的疫苗数量都是有限的.实践中，一方面，随着人群中易感者比率的增加接种比率也会增加，但不会无限地增加，一旦达到所能提供的疫苗的最大数量，就会维持在这个水平不变.另一方面，传染病爆发时，因为价格偏高、防疫意识差导致相当一部分人不愿接种疫苗.例如，2009年当甲型H1N1爆发时，一家媒体调查显示有54%的人都不愿接种疫苗.基于此，本文采用1个含有阈值参数的饱和函数表示接种比例，以刻画接种策略仅对于自愿接种的人有效，且医疗资源允许下的接种人数是有限的.将人群分为3大类:易感者、感染者和接种疫苗的人，则模型为

其中S，I，V分别表示人群中易感者、染病者和接种疫苗者的比例，假设接种后将终生具有免疫力.为免疫接种函数，ST表示不愿接种的人占人群总数的比例，h表示该地区存储疫苗所能接种的易感者的最大比例.注意到1个地区拒绝接种的人毕竟是少数，而所存储疫苗能接种的最大人数往往比较大，所以假设h＞ST是合理的.其他参数均为正数，其中μ表示自然出生率(自然死亡率)，β表示传染率，ε表示对染病者的治愈率，并且假设一旦治愈将终身具有免疫力.实践中人群的输入率总是大于该地区所存储疫苗能最多接种的易感者比例，从而总可以假设μ＞h.

注意到V不影响前2个方程的动力学，故以下只须考虑简化方程

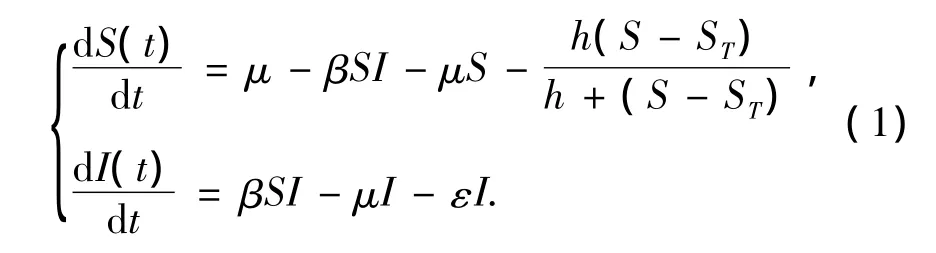
不难证明以下结论:

1 平衡态的存在性

模型(1)的无病平衡点满足方程

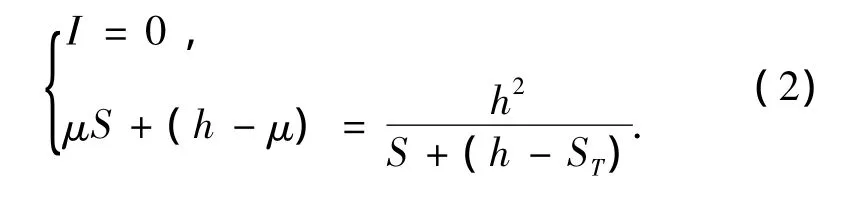
为讨论方便起见，以下记

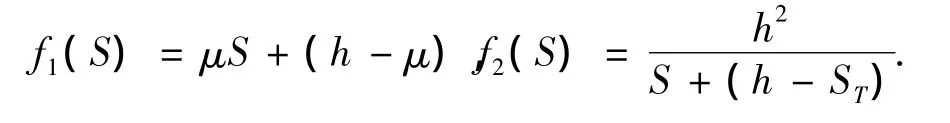
(2)式的第2个方程具有正根的条件等价于f1(0)＜f2(0)，由于

所以模型(1)恒存在1个无病平衡点E0(S0，0)，其中，

若模型(1)存在地方病平衡点E*(S*，I*)，则其满足

由于(μ-h)-μS*+h2［h+(S*-ST)］＞0等价于［μ(μ +ε)-β(μ -h)］［β(h-ST)+(μ +ε)］＜β2h2，故有以下2种情况:

(i)当μ(μ+ε)-β(μ-h)≤0时，方程(4)的解恒为正，此时模型(1)存在唯一的地方病平衡点.

(ii)当μ(μ+ε)-β(μ-h)＞0时，则

从而(4)式存在唯一正解，即模型(1)存在唯一的地方病平衡点.

综上讨论，可得如下结果:

定理1(i)模型(1)存在唯一的无病平衡点E0(S0，0)，其中 S0如(3)式所定义.

(ii)若以下任意1组条件成立:

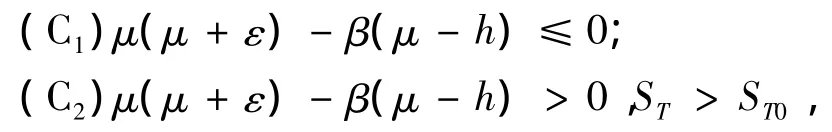
则模型(2)存在唯一的地方病平衡点E*(S*，I*)，这里S*如(4)式所定义，

注意到

故I*随着阈值ST的增加而增加，即疫情稳定后染病者的比例随着人群中不愿接种疫苗的人的比例增加而增加.因为不愿接种疫苗的人在人群中的比例会随着周围环境的变化而变化，如媒体的宣传和教育、季节的变化、疫情等，所以这里将它作为1个阈值，以考虑其对于染病者的比例等因素的影响.

直接计算可得模型(1)的基本再生数为R0=βS0(μ+ε)，其中S0由(3)式给出.从而，

注意到

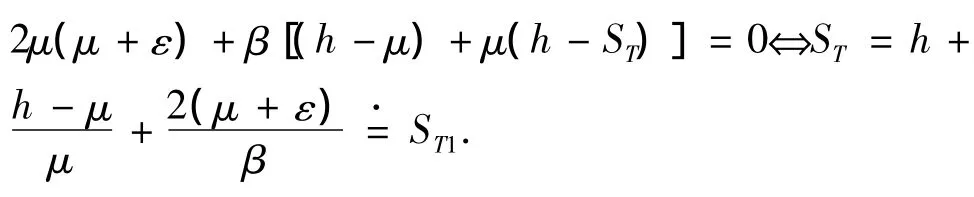
下面分2种情况讨论:

(i)若ST≥ST1，则由(5)式知R0＞1.

(ii)若ST＜ ST1，则当

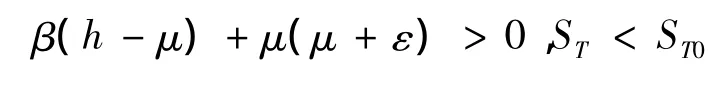
或者

时，均有R0＜1.由于

所以当β(h-μ)+μ(μ +ε)＞ 0时，ST0＜ ST1;当β(h-μ)+μ(μ+ε)＜ 0时，ST0＞ ST1.由此有以下结论:

定理2 R0＜1的充要条件为

由于

所以R0是ST的递增函数.

综合以上讨论，可得如下结果:

推论1(i)R0＞1当且仅当(C1)或(C2)成立;(ii)模型(1)存在地方病平衡点的充要条件为R0＞1;(iii)R0和I*均随着ST的增加而增加，如图1所示.

2 全局稳定性

本节主要讨论模型(1)的无病平衡点以及地方病平衡点的全局稳定性.为此，首先排除极限环的存在性.

引理2 模型(1)在吸引域Ω内不存在极限环.

证 为方便讨论，引入记号

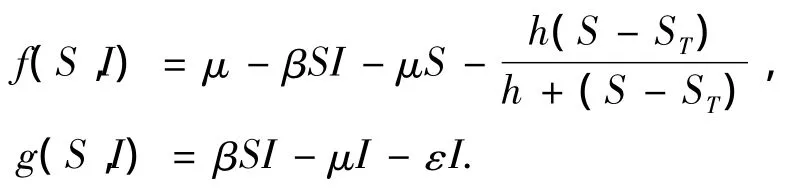
取Dulac函数B=1/(SI)，则有

由Bendixson-Dulac原理知，模型不存在全部位于Ω内的极限环.引理2得证.

定理3 当R0＜1时，模型(1)的无病平衡点E0全局渐近稳定，此时疾病将最终被消除.

证 模型(1)的雅克比矩阵为

直接计算得J(S0，0)的2个特征根分别为

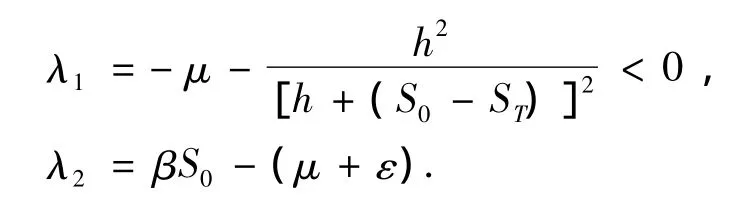
当R0＜1时，λ2＜0，从而E0局部渐近稳定.根据引理2，模型(1)在吸引域内不存在极限环，所以E0是全局渐近稳定的，如图2(a)所示.此时，疾病将最终被灭绝，而人群中易感者的比例趋于1个稳定的水平S0，如图2(b)所示.定理3得证.

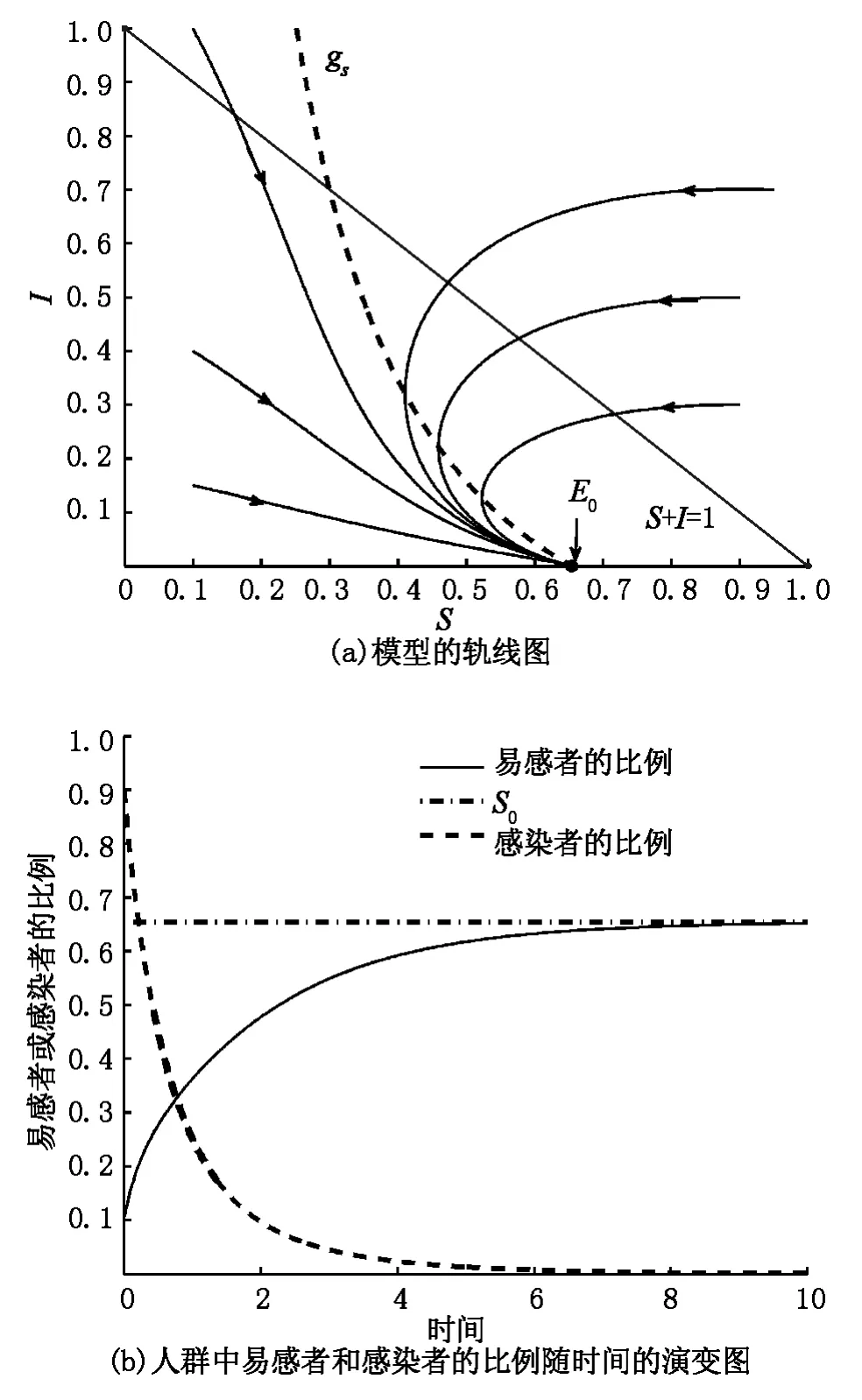
图2 当参数值为μ =0.6，β =2，h=0.5，ST=0.3，ε=1.2，R0＜1时模型(1)的稳定性

由推论1知当R0＞1时，模型(2)存在唯一的地方病平衡点E*，下面讨论E*的稳定性.由(6)式知，

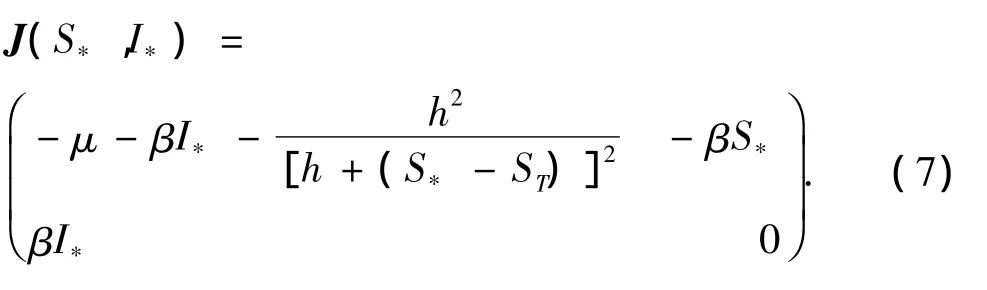
由于 tr(J(S*，I*))=-μ-βI*-h2［h+(S*-ST)］2＜ 0，det(J(S*，I*))= β2S*I*＞ 0，所以(7)式有2个具有负实部的特征根，从而地方病平衡点E*局部渐近稳定.又根据引理2知，E*是全局渐近稳定的，如图3(a)所示.此时，人群中易感者和感染者的比例(S和I)达到一个静态平衡，即S和I分别趋于稳定的水平S*和I*，如图3(b)所示.从而有结论:

定理4 当R0＞1时，模型(1)的地方病平衡点E*全局渐近稳定.此时，疾病将最终演变为地方病.

图3 当参数值为μ =0.6，β =4，h=0.5，ST=0.3，ε=0.8，R0＞1时模型(2)的稳定性

3 结论

考虑到实践中有相当一部分人因为价格偏高、免疫意识低下等原因不愿接种疫苗，本文引入1个阈值参数，建立了1个具有饱和接种率的传染病模型，以刻画医疗资源有限情况下的接种策略.得到了各类平衡点存在的条件阈值R0.当R0＜1时，即1个病人在平均患病期内所传染的人数小于1，疾病最终会消失;而当R0＞1时，即1个病人在平均患病期内所传染的人数大于1，疾病不会被消除，而将始终存在，最终成为一种地方病.由R0，I*的表达式及推论1知，当人群中不愿接种的人所占的比例增加时，基本再生数R0增加，I*也增加.这说明一方面要使疾病最终被消除，就必须进行相应的宣传和教育，提高民众的危机意识，使更多的人自发接种疫苗，从而减少不愿接种疫苗的人的数量.另一方面，当疾病不能被消除时，通过降低人群中抵触接种疫苗的人的比例，可以使得染病者的比例稳定在一个预先设定的水平，从而为公共卫生部门制定传染病的控制策略提供理论支撑.因为实际控制中，往往不需要将病毒彻底清除，只需将人群中已感染者的比例降至医疗规范允许的水平之下.

由定理3和定理4知，疾病是否被消除取决于基本再生数R0是否小于1.而由R0的表达式及定理2知，R0是否小于1取决于不愿接种疫苗的人的比例是否小于临界值ST0，而ST0的大小依赖于1个国家或地区的疫苗的最大存储量(用h刻画).又由于

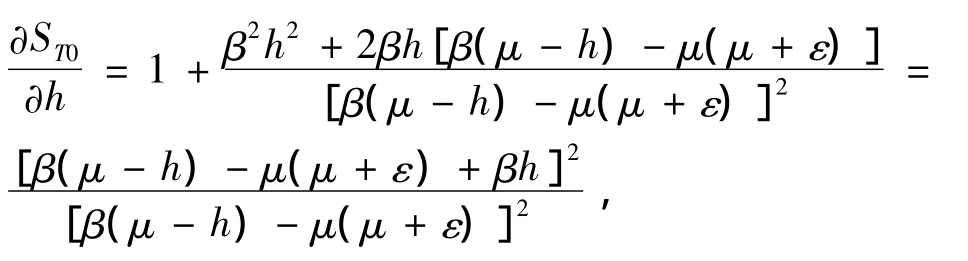
所以ST0随着h的增大而增大.这意味着如果人群中抵触接种的人的比例保持不变，当疫苗的最大存储量足够大时，疾病最终也会被消除.

综上所述，人群中不愿接种疫苗的人的比例和一个国家或地区的疫苗的最大存储量对疾病消除以及当疾病不能被消除时染病者所占比例有很大的影响，所以考虑这2个因素对于疾病控制的影响非常必要且具有重要意义.

［1］ Anderson R，May R.Infectious disease of humans，dynamics and control［M］.Oxford:Oxford University Press，1995.

［2］Keeling M J，Rohani P.Modeling infectious diseases in human and animals［M］.Princeton:Princeton University Press，2008.

［3］赵君平.一类具有一般非线性隔离函数和潜伏年龄SEIRS传染病模型稳定性分析［J］.江西师范大学学报:自然科学版，2011，35(5):464-470.

［4］马知恩，周义仓，王稳地.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004.

［5］Wang Wendi.Backward bifurcation of an epidemic model with treatment［J］.Math Biosci，2006，201(1):58-71.

［6］万辉，李永凤.一类传染病模型的Bagdanov-Takens分支分析［J］.南京师大学报:自然科学版，2012，35(4):7-13.

［7］Li Yongfeng，Cui Jingan.The effect of constant and pulse vaccination on SIS epidemic models incorporating media coverage［J］.Comm Nonl Sci Nume Simu，2009，14(5):2353-2365.

［8］Greenhalgh D，Khan Q JA，Lewis F I.Recurrentepidemic cycles in an infectious diseasemodel with a time delay in loss of vaccine immunity［J］.Nonl Anal TMA，2005，63(6):779-788.

［9］Xiao Yanni，Tang Sanyi.Dynamics of infection with nonlinear incidence in a simple vaccination model［J］.Nonlinear Anal，RWA，2010，11(5):4154-4163.

［10］Buonomo B.On the optimal vaccination strategies for horizontally and vertically transmitted infectious diseases［J］.JBiol Syst，2011，19(2):263-279.

［11］Onofrio A d'.Stability properties of pulse vaccination strategy in SEIR epidemic model［J］.Math Bios，2002，179(1):57-72.

［12］Wang Aili，Xiao Yanni.Sliding bifurcation and global dynamics of a Filippov epidemic model with vaccination［J］.Internat JBifur Chaos，2013，23(8):1-32.

［13］Stone L，Shulgin B，Agur Z.Theoretical examination of the pulse vaccination policy in the SIR epidemic model［J］.Math Comp Mode，2000，31(4):207-215.

［14］Hui Jing，Chen Lansun.Impulsive vaccination of SIR epidemic models with nonlinear incidence rates［J］.Disc Cont Dyna Syst，2004，4(3):595-605.

［15］Arino J，Mccluskey C C，Driessche P V D.Global results for an epidemicmodelwith vaccination thatexhibits backward bifurcation ［J］.SIAM JAppl Math，2003，64(1):260-276.