基于融合信息熵性质的信任函数概率逼近

程子成，吴根秀，宋姝婷

(江西师范大学数学与信息科学学院，江西南昌 330022)

0 引言

不确定性推理是人工智能及有关领域中一个重要的课题［1］.而D-S证据理论是不确定性推理的主要方法，如何运用D-S证据理论基于信任函数做出可靠性决策，依然是一个有待解决的问题.将信任函数转化为概率函数进行决策是一个简单可行的方法.不少学者在这方面进行了相关的研究［2-3］，其中P.Smets等［4］提出Pignistic概率转化得到了广泛的应用，它是基于最小承诺原则，即把信息不确定性最大化情况下做决策，也是一种最保守的决策，其他学者［5-11］在此基础上进行了相应的改进，使得转换以后做决策时信息不确定性更小.

在信息理论中，信息熵用来衡量信息源的不确定性大小，为信任函数转化为概率函数做决策的可靠性提供了评价标准.为此本文研究信息熵的若干性质，给出了几个定理及推论，然后提出了一种新的信任函数概率逼近方法.在对信任函数概率逼近过程中融合信息熵的性质，以Pignistic概率为初始值，逐步逼近，使得每步下去信息熵不断减小.通过与现有的方法比较，本文方法都能得到较好的决策效果.

1 证据理论基本概念

设非空集合Θ为识别框架，定义映射m:2Θ→［0，1］，满足:，称m为基本概率分配函数(mass函数)，如果m(A)＞0，则称A为焦元.

信任函数Bel定义为

它表示对A的信任度.

似然函数Pl定义为

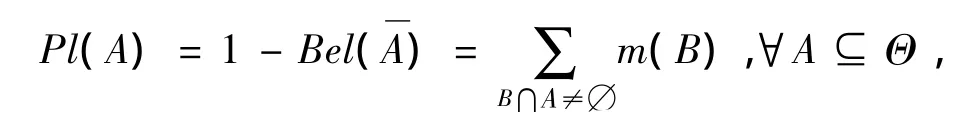
它表示不怀疑A的程度，即A似真的程度.显然有Bel(A)≤ Pl(A)，并且区间［Bel(A)，Pl(A)］表示对A信任程度的区间估计.本文把2Θ中单点集称为子命题，而非单点集称为复合命题，信任函数概率逼近即把mass函数对所有命题的支持度转化为对子命题的概率测度，且满足

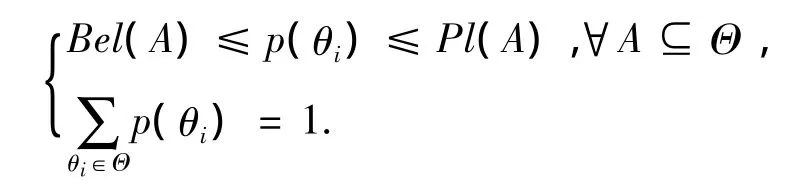
2 现有信任函数概率逼近方法及评价指标

2.1 Pignistic概率转换

Pignistic概率转换的目的是对系统已获得的各命题的信度值进行重新分配以获得更可靠的决策依据.设识别框架 Θ ={θ1，θ2，…，θn}，m 是 Θ 上的基本概率分配函数，定义如下:

2.2 Sudano’s转换方法

Sudano’s通过对基本信任函数值的不同分配途径提出了一些概率转换方法，这些方法分别为

2.3 DSmP概率转换方法

Dezert等［7］基于对Pignistic概率转换的修正并提出了DSmP概率转换方法:

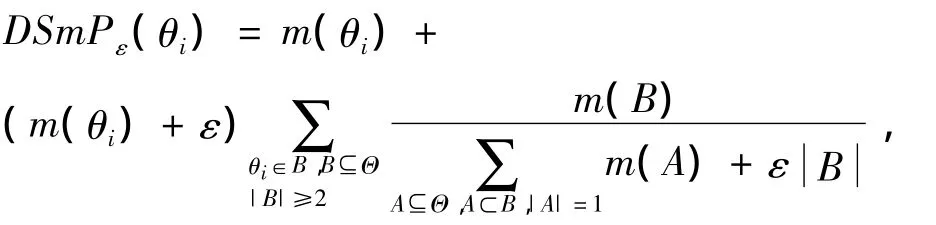
其中ε是调节参数，当焦元不存在单点集时，DSmP概率等价于Pignistic概率.

2.4 Han’s转换方法

Han’s［11］以信息熵建立目标函数，给定约束条件寻找使得目标函数值达到最小的最优解，即为信任函数概率转换，记为Un_min，其定义如下:

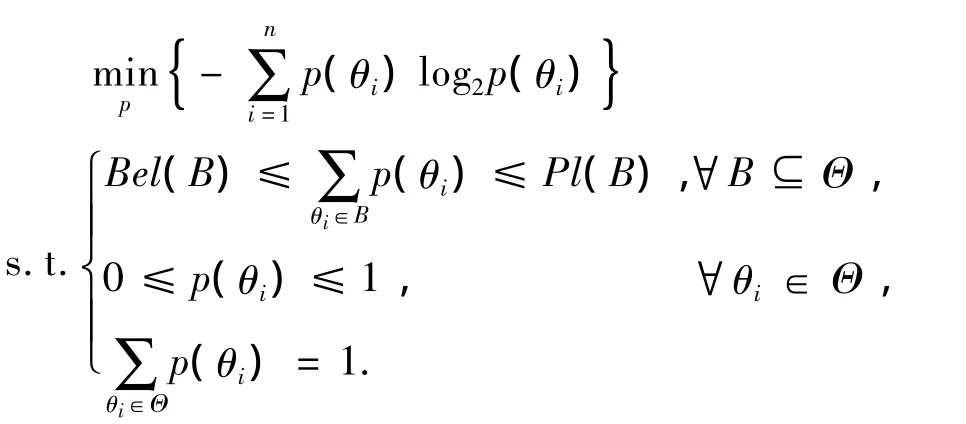
当识别框架Θ很大时，随子集个数增加，约束条件就会很多，则计算复杂度将很高，并且在某些特殊的情况下会出现不合常理的结论，增加了决策的风险.

2.5 信任函数概率逼近的评价指标

在D-S证据理论中对信任函数进行概率逼近，即把对所有命题的信任度转化为对子命题的概率测度.若对所有子命题的概率都一样，则认为在逼近过程中失去了有用的信息，此时概率分布所包含子命题的信息不确定性达到最大，即命题中的信息等可能的支持所有子命题，此时决策结果是不可靠的.而均匀分布为等可能支持子命题的概率分布.假设N个子命题{H1，H2，…，HN}所对应的概率值为p(1)，p(2)，…，p(N)与均匀分布U做比较，可以用Kullback-Leibler距离度量2者之间的差异

因此，

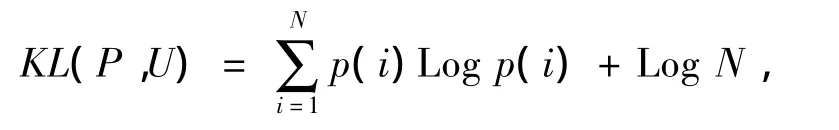
对上面等式进行标准化后称为概率信息含量(probability information content，PIC):

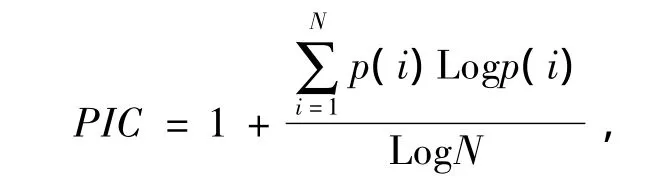
其中规定0Log 0=0，则 PIC 取值范围为［0，1］，当PIC=0时，概率分布P所具有的信息不确定性最大，基于概率分布P无法做出正确决策;当PIC=1时，概率分布P所具有的信息最确定，能够做出正确的决策.为此可利用PIC作为信任函数做概率逼近的质量以及用于决策可靠性的度量［12-14］.

3 信息熵相关性质与信任函数概率逐步逼近法

3.1 信息熵相关性质的研究

在信息理论中，信息熵用来衡量信息源的不确定性大小，设 Θ 上的概率分布 p1，p2，…，pn，定义信息熵为

Hn(p1，p2，…，pn)取值为［0，log2n］，由信息熵的定义可以得到一些简单的性质:

由信息熵的定义与相关的性质，给出下面结论.

引理1 若0≤p3≤p2≤p1≤1且p1+p2+p3=1，则H2(p1+p2，p3)≤H2(p1+p3，p2)≤H2(p1，p2+p3).

证 设函数f(u)=-u log2u-(1-u)log2(1-u)，u∈［0，1］，记 0 log20=0.令 x=p1+p2，y=p1+p3，z=p2+p3，则有 f(x)=H2(p1+p2，p3)，f(y)=H2(p1+p3，p2)，f(z)=H2(p1，p2+p3)，且0≤z≤y≤x，1/2 ＜y≤x≤1.因为f(u)在区间［1/2，1］内单调递减，有f(x)≤ f(y)，即 H2(p1+p2，p3)≤ H2(p1+p3，p2).由题意可知p2≤p2+p3，即1-y≤z≤1/2，又因函数f(u)关于u=1/2对称，有f(y)=f(1-y)，且在区间［0，1/2］内单调递增，有f(y)≤f(z)，即

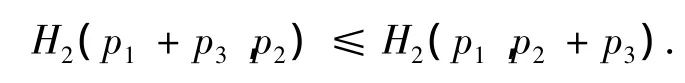
综上所述

定理1 设0≤p1，…，pn≤1且，若p3≤ p2≤ p1，则

证 先证左边不等式

因为

故只需证明

即

两边同时减去(p1+p2+p3)log2(p1+p2+p3)化简得到

两边同时除以(p1+p2+p3)得

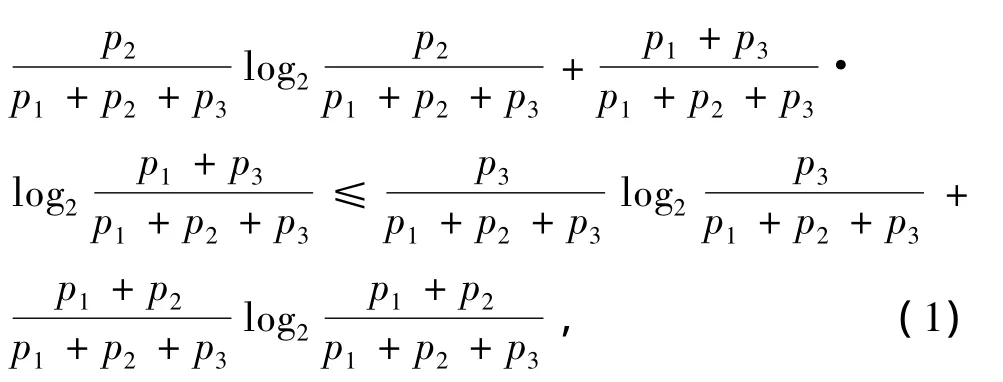
令p'1=p1/(p1+p2+p3)，p'2=p2/(p1+p2+p3)，p'3=p3/(p1+p2+p3)，由(1)式得

因为0≤p'3≤p'2≤p'1且p'3+p'2+p'1=1，由引理1可知

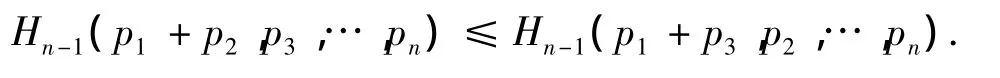
同理可证

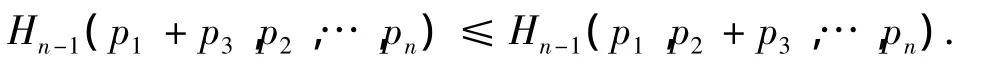
定理1得证.

推论1 设0≤p1，…，pn，若∀ε，满足0≤ ε≤ p2≤ p1，则

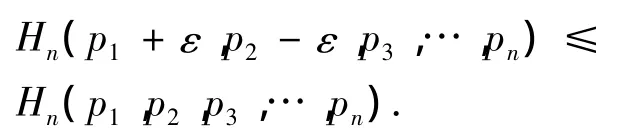
证 对任意满足题意的ε，都有p1+(p2-ε)+ε+p3+…+pn=1且存在不等式ε≤p2-ε≤p1或者p2-ε≤ε≤p1，由定理1可知，Hn(p1+ε，p2-ε，p3，…，pn)≤ Hn(p1，p2- ε + ε，p3，…，pn)=Hn(p1，p2，p3，…，pn).

推论2 设0≤p1，…，pn≤1且，若∀ε2，ε3，…，εn，满足0 ≤εi≤pi≤p1(i=2，…，n)，则

证 反复应用推论1可得结论成立.

由信息熵的性质定理1及2个推论可知，当信息支持大概率事件时，不确定性逐渐减少，推理结论的确定性程度增大.因此，在信任函数概率逼近过程中信息应该朝着与支持度大的事件融合，然后进行决策.

3.2 信任函数概率逐步逼近方法

识别框架Θ上的基本概率分配函数对所有命题都有个支持度(或信任度).当信任函数进行概率逼近时(即信息转移过程)，对子命题的支持度也随着变化，为此定义条件支持度的概念，它度量信任函数逼近过程中对子命题的支持度的变化.

定义1 设识别框架Θ，给定C，θi(θi∈C，C⊆Θ)，∀θj(θj∈ C)定义

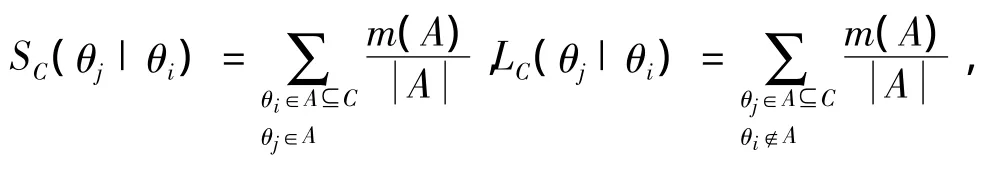
则称SC(θj|θi)与LC(θj|θi)分别为m在C上提取信息θi(目标子命题)对θj的条件支持度与剩余支持度.记SC(θi)=SC(θi|θi)为m在C上对θi的无条件支持度，显然有SΘ(θi)=BetPm(θi);记LC(θi)=LC(θi|θi)=0，即m在C上提取θi信息后对θi的剩余支持度为0.由定义1显然有下面性质.

性质1 给定 C(C ⊆ Θ)，∀θj，θi∈ C，有

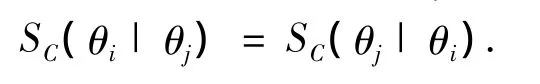
性质 2 ∀θj，θi∈ C，有

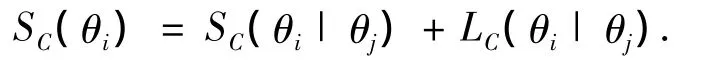
性质 3 ∀θj，θi∈ C(i≠ j)，有

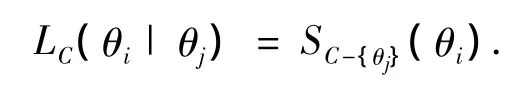
性质1说明m在C上对子命题的条件支持度是相互的.性质2表明当对子命题的无条件支持度一定时，子命题的条件支持度越大，则其剩余支持度就越小.从性质3可以看出m在C上目标子命题对子命题的剩余支持度即为m在C上提取目标子命题信息后对子命题的无条件支持度.于是本文给出新的信任函数的概率逼近算法，该算法是以Pignistic概率逼近为基础，逐步提取子命题条件支持度，并将其聚焦于无条件支持度大的子命题.

首先选取Pignistic概率作为信任函数初始逼近，然后计算每个子命题的条件支持度，选取条件支持度最大的子命题进行信息聚合，再重新计算每个原子命题的条件支持度，直到所有信息融合完成为止，下面给出具体算法.

输入:Θ ={θ1，θ2，…，θn}，Θ 上的 mass值;

初始条件:I={1，2，…，n}，C= Θ;

第1步 计算每个子命题θi∈Θ的无条件支持度，令 pi=SΘ(θi)，得到概率分布(p1，p2，…，pn)为信任函数的初始概率逼近，即为Pignistic概率逼近;

第2步 取 i0=argmax{pi|i∈ I}，∀θi∈C(i≠i0)，计算条件支持度与剩余支持度:

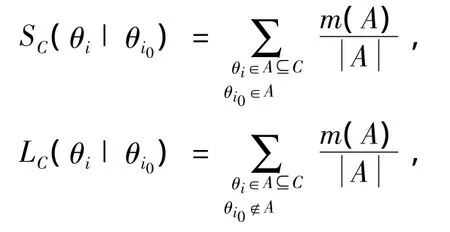
当i=i0时，pi←pi+)，当 i∈ I-i0时，pi← pi-S(θi|θi0)=LC(θi| θi0)，当 i∉ I时，pi←pi，记I←I-{i0}，C←C-{θi0}，则(p1，p2，…，pn)为信任函数中提取信息θi0后的概率逼近;

由推论2可知，在逐步逼近法算法中每做一步逼近，信息熵都比上一步小，即不确定性降低，所以与Pignistic概率方法比较，本文方法最终得到的信息熵更小，而且每一步得到的概率分布都是相容概率.在实际应用中根据决策者的需要可以对转化过程进行相应的控制，这可以降低决策的高风险性.

4 实例分析

例 1 设识别框架 Θ ={θ1，θ2，θ3，θ4}，基本概率分 配 值:m({θ1})=0.16，m({θ2})=0.14，m({θ3})=0.01，m({θ4})=0.02，m({θ1，θ2})=0.20，m({θ1，θ3})=0.09，m({θ1，θ4})=0.04，m({θ2，θ3})=0.04，m({θ2，θ4})=0.02，m({θ3，θ4})=0.01，m({θ1，θ2，θ3})=0.10，m({θ1，θ2，θ4})=0.03，m({θ1，θ3，θ4})=0.03，m({θ2，θ3，θ4})=0.03，m({Θ})=0.08.

运用本文方法计算例1得出结果，且将该结果与其它方法计算的结果做比较(见表1).

表1 信任函数概率逼近结果

从表1可以看出本文的逼近方法在决策结果上能与其它方法保持一致，并且有着更大的PIC值，且该方法计算得到的结果与Han’s提出的Un_min方法得到的结果完全一致，它不仅融合了信息熵的性质，而且从条件支持度、信息提取量角度进行逼近，同样得到较好的决策效果.

为了降低由逼近所带来的决策高风险性，本文方法可以根据决策者的决策需要对上一步逼近的结果选取最大值进行下一步逼近时设定阀值α，若最大值与第2大值之差在阀值内可以停止逼近，否则可以继续下去.降低了Un_min的方法逼近过程不可控制所带来的决策高风险性.

例 2［11］设识别框架 Θ ={θ1，θ2}，mass 值m({θ1})=0.100 01，m({θ2})=0.100 00，m({θ1，θ2})=0.799 99.

用Han的Un_min方法逼近结果为p(θ1)=0.9，p(θ2)=0.1，此结果有悖于直觉，没有理由把所有的信度值都分配给θ1，做这样的决策风险太大.而本文的方法:第1步计算每个子命题的无条件支持度(即 Pginistic概率)为 p(θ1)=0.500 005，p(θ2)=0.499 995，假设阀值为 α =0.001，因为p(θ1)-p(θ2)=0.000 000 1 ＜ α，则可以停止接下去的逼近，最终逼近结果为Pignistic概率，符合直觉的判断，降低了决策风险.

5 结论

信任函数概率逼近可以认为对信任函数的概率近似，以此得到更好的决策效果.本文从信息熵的性质出发，提出了信任函数概率逼近的新方法，以Pignistic概率为初始值融合信息熵的性质进行逐步逼近，逼近后的概率能够包含更多确定信息，为了降低决策的高风险性，给定阀值以此决定逼近过程.通过算例说明本文的方法与其它方法逼近后的决策结果能保持一致，这表明本文方法的可行性.

［1］黄林颖，吴根秀，万宁文，等.信任函数的逼近［J］.江西师范大学学报;自然科学版，2006，30(1):58-62.

［2］蒋雯，吴翠翠，贾佳，等.D-S证据理论中的基本概率赋值转换概率方法研究［J］.西北工业大学学报，2013，31(2):295-299.

［3］王万请，赵拥军，黄洁，等.基于不确定度的基本概率赋值概率转换方法［J］.控制与决策，2013，28(8):1214-1218.

［4］Smets P，Kennes R.The transferable beliefmodel［J］.Artifial Intelligence，1994，66(2):191-234.

［5］ Sudano J J.The system probability information content(PIC)relationship to contributing components，combining independentmulti-source beliefs，hybrid and pedig-ree pignistic probabilities［C］∥2002 Proceedings of the Fifth International Conference on Information Fusion.IEEE，2002:1277-1283.

［6］Sudano J.Pignistic probability transforms formixes of lowand high-probability events ［J］.Proc of Fusion，2001，2001:23-27.

［7］Dezert J，Smarandache F.A new probabilistic transformation of beliefmass assignment［C］∥2008 11th International Conference on Information Fusion.IEEE，2008:1-8.

［8］ Sudano J，Martin L.Equivalence between belief theories and naive Bayesian fusion for systems with independent evidential data-Part I，the theory ［J］.Proc of Fusion，2003，2003:1239-1243.

［9］Sudano JJ，Martin L.Yetanother paradigm illustrating evidence fusion(YAPIEF)［C］∥2006 9th International Conference on Information Fusion.IEEE，2006:1-7.

［10］Cuzzolin F.On the properties of the Intersection proba-Bility［J］.Submitted to the Annals of Mathematics and AI，2007(1):1-34.

［11］Han Deqiang，Dezert J，Han Chongzhao，etal.Is entropy enough to evaluate the probability transformation approach of belief function?［C］∥Proc of International Conference on Information Fusion.IEEE，2010:1-7.

［12］Zhou Zhe，Yang Chunjie，Wen Chenglin.Belief function to probability:A tradeoff between easy decision-making and high risk［C］∥2013 10th IEEE International Conference on Control and Automation(ICCA).IEEE，2013:233-237.

［13］韩德强，杨艺，韩崇昭.D-S证据理论研究进展及相关问题探讨［J］.控制与决策，2014，29(1):1-7.

［14］刁联旺，李勇智，杨静宁.D-S证据推理的决策问题［J］.计算机工程与应用，2003，39(33):82-84，97.