Adomian分解法求解非线性分数阶Volterra积分方程

全晓静，韩惠丽，王 健

(宁夏大学数学计算机学院，宁夏 银川 750021)

QUAN Xiao-jing，HAN Hui-li* ，WANG Jian

(School of Mathematics and Computer Science，Ningxia University，Yinchuan Ningxia 750021，China)

0 引言

分数阶微积分理论已经逐渐完善，自Leibinz开始考虑分数阶概念以来，分数阶微积分被国内外学者广泛的研究.近年来，分数阶微积分被广泛的应用在混沌系统、粘弹性力学等问题中，这些问题经过建模后得到的方程大多数都是分数阶积分微分方程或者分数阶积分方程，对于这种方程来说，求其解析解是相当困难的，甚至很多方程根本没有解析解.因此，对于分数阶积分方程数值解法国内外学者提出了配置法、Legendre多项式、小波法等［1-2］求解方法.

Adomian分解法自从被提出以来，广泛应用于线性和非线性的数学物理方程的求解中，尤其是求解动力系统问题.G.Adomian［3-4］给出了Adomian分解法的基本思想并用它求解一些动力系统的数值逼近解.梁祖峰等［5］用Adomian分解法求解分数阻尼梁的解析解，与传统的数值方法比较发现Adomian分解法不需要借助线性化、摄动或一些限制性的假设［6］.因此，Adomian方法被许多学者广泛应用.近年来，用Adomian分解法逼近非线性方程的解析解(如ODEs、PDEs、积分方程和积分微分方程)更显优势［7-9］.2008 年 I.L.El-Kalla［7］运用 Adomian 分解法逼近非线性Volterra积分方程的解析解，2010年S.H.Behiry等［8］对非线性Fredholm积分方程用离散的Adomian分解法逼近.但是在非线性分数阶领域

1 Adomian分解法

考虑非线性分数阶Volterra积分方程［10］

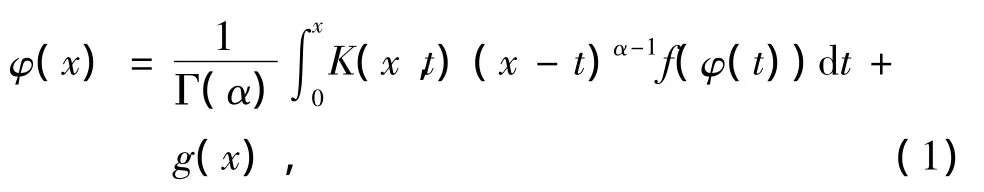
其中，Γ(α)是Gamma函数(α ＞ 0)，K(x，t)和g(x)是已知函数，g(x)在∀x∈I=［0，1］上有界，且为正整数.φ(x)是未知的连续函数，非线性项f(φ)满足Lipschiz条件，∃L＞0，使得

非线性项f(φ)可由Adomian多项式［6］表示为

其中

部分和Sn定义为

这里

因此，对(1)式运用Adomian分解法，将方程的解研究甚少，本文采用Adomian分解法求解非线性分数阶Volterra积分方程的数值解.φ(x)分解为无穷个分量和的形式，即

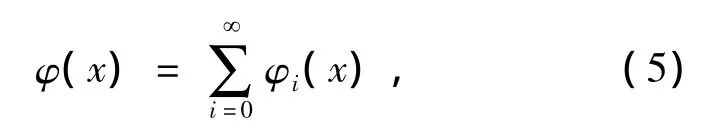
将(2)式和(5)式代入(1)式得ADM递推公式:

(5)式即为(1)式的级数解，接下来证明(5)式级数解收敛到方程的精确解.

2 收敛性分析

定义映射 T:E→E，其中E=(C［I］，‖·‖)为区间I上所有连续函数组成的Banach空间，定义该空间上的范数为

定理1 积分方程(1)存在唯一解当且仅当0＜β＜1，其中β=LMΓ(α+1).

证 映射T:E→E定义为

∀φ，ψ ∈ E，有

当0＜β＜1时，T为压缩映射，由Banach压缩映射定理可知，(1)式存在唯一解.定理1得证.

定理2 积分方程(1)式的级数解(5)式是收敛的当且仅当0＜β＜1，且g(x)是有界函数.

证 令Sn，Sm为(5)式的任一部分和，且n＞m，Banach空间中只需证明{Sn}是 Cauchy列.由(4)式可知，

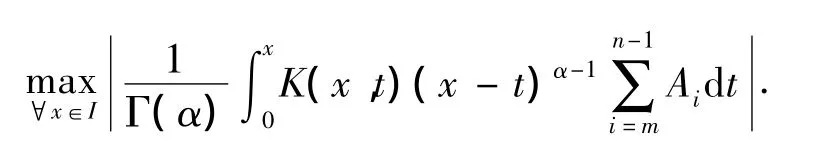
由(3)式可知，

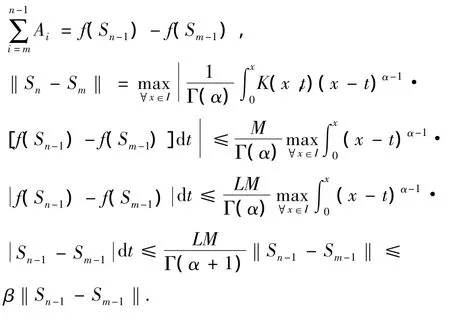
令 n=m+1，可得

由三角不等式可知，

因为0＜β＜1，所以(1-βn-m)＜1，可得

3 误差分析

定理3 方程(1)式的级数解(5)式的最大绝对截断误差为

当n→∞时，得

由(4)式可得

定理3得证.

4 数值算例

例1 考虑非线性分数阶Volterra积分方程

其中α =2.5，且

分别取 m=1，m=2，m=3，数值解与精确解的绝对误差如表1所示.

表1 数值解与精确解的绝对误差

例2 考虑非线性分数阶Volterra积分方程

分别取m=1，m=2，m=3，表2给出了本文方法的数值解与精确解的绝对误差.

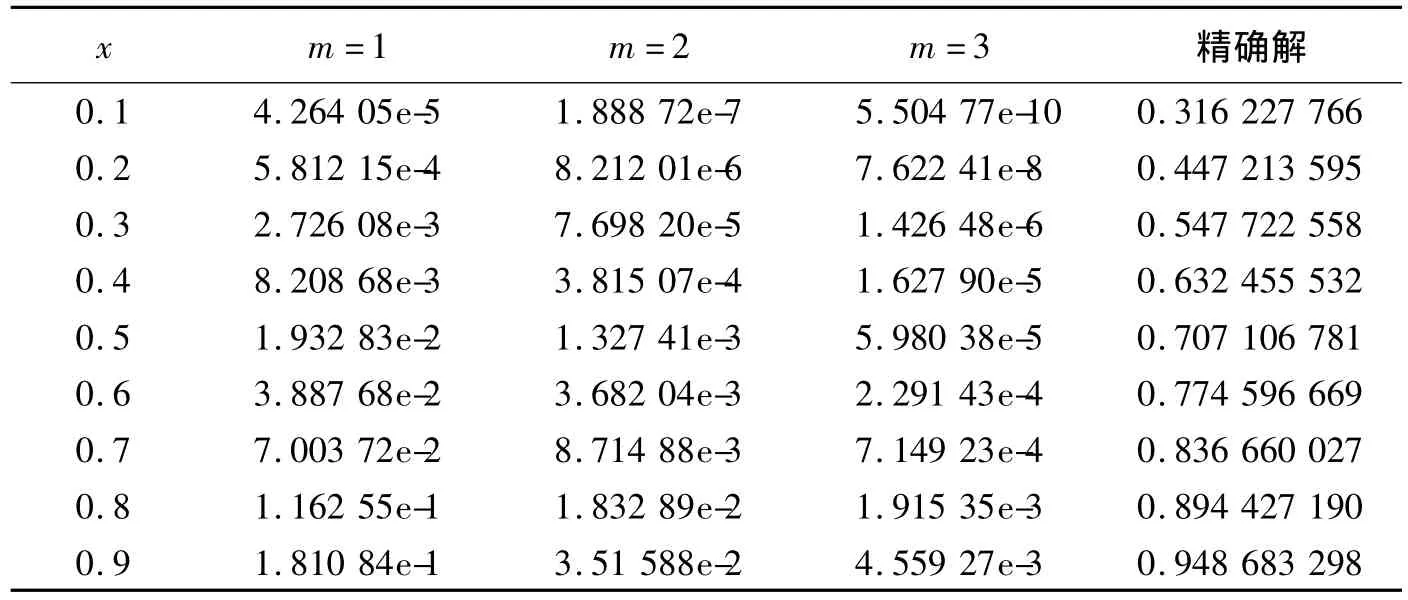
表2 数值解与精确解的绝对误差

由表1和表2可以发现，通过计算较少的Adomian多项式就可以有效地逼近非线性分数阶Volterra积分方程的精确解.随着m值的增大，绝对误差越来越小，且收敛速度越快.

5 结论与展望

本文利用Adomian分解法求解了非线性分数阶Volterra积分方程，通过收敛性分析证明了Adomian级数解在一定条件下收敛到方程的解析解，并给出了级数解的最大截断误差，最后通过数值算例验证了该方法的有效行和可行性.同样，可以将这种方法用来求解非线性分数阶Fredholm积分方程［11-15］的数值解.

［1］ Lepik U¨.Sloving fractional integral equation by the Haar waveletmethod ［J］.Applied Mathematics and Computation，2009，214(2):468-478.

［2］朱双云，苗福生，韩惠丽.分数阶第一类Volterra积分方程小波数值解［J］.宁夏大学学报:自然科学版，2012，33(2):130-134.

［3］Adomian G.Stochastic system［M］.New York:Academic Press，1983.

［4］Adomian G.A review of decomposition method in applied mathematics［J］.Joural of Mathematics Analysis and Application，1988，135(2):501-544.

［5］梁祖峰，唐晓艳.用Adomian分解法求解分数阻尼梁的解析解［J］.应用数学和力学，2007，28(2):200-208.

［6］Duan Junsheng，Randolph Rach，Dumitru Baleanu，et al.A review of the Adomian decomposition method and its applications to fractional differential equations［J］.Commun Frac Calc，2012，3(2):73-99.

［7］El-Kalla IL.Convergence of the Adomian method applied to a class of nonlinear integral equations［J］.Applied Mathematics Letters，2008，21(4):372-376.

［8］ Behiry S H，Abd-Elmonem R A，Gomaa A M.Discrete Adomian decomposition solution of nonlinear fredholm integral equation ［J］.Ain Shams Engineering Journal，2010，1(1):97-101.

［9］单锐，魏金侠，张雁，等.Adomian分解法求解二维非线性Volterra积分方程的数值解［J］.黑龙江大学自然科学学报，2012，29(5):573-577.

［10］黄洁，韩惠丽.应用Legendre小波求解非线性分数阶Volterra积分微分方程［J］.吉林大学学报:理学版，2014，52(4):655-660.

［11］张倩，韩惠丽，张盼盼.基于有理Haar小波求解分数阶第2类Fredholm积分方程［J］.江西师范大学学报:自然科学版，2014，38(1):47-50.

［12］陈一鸣，刘丽丽，孙璐，等.Adomain分解法求解非线性分数阶Fredholm积分微分方程［J］.应用数学，2013，26(4):785-790.

［13］朱红玲，郝玲，余志先，等.Adomain分解法求解非线性分数阶积分微分方程［J］.辽宁工程技术大学学报:自然科学版，2013，32(1):132-135.

［14］陈一鸣，孙慧，刘乐春，等.Legendre多项式求解变系数的分数阶Fredholm积分微分方程［J］.山东大学学报:理学版，2013，48(6):80-86.

［15］仪明旭，陈一鸣，魏金侠，等.应用Haar小波求解非线性分数阶Fredholm积分微分方程［J］.河北师范大学学报:自然科学版，2012，36(5):452-455.