强激光脉冲在部分离化等离子体中的自聚焦

柳剑鹏，陶志鹏，陶向阳

(江西师范大学物理与通信电子学院，江西南昌330022)

0 引言

获得能散度较低、能量较高的电子束，一直是激光等离子体领域中的研究热点.经过多年的理论与实验研究，相关领域科学工作者们已经取得了较大的进步.2002年V.Malka等在实验中得到了能量高达200 MeV的准直高能电子束［1］，但能散较高;同年，A.Pukhov等通过PIC方法发现，在一定条件下，可通过尾波场加速获得满足实际所需的高质量电子束［2］;2004年，英美等国科学家实验上获得了能散度为2%～24%，能量在80～170 MeV之间的电子束［3－4］.强激光在等离子体中的稳定传播有着广泛的应用，如激光核聚变［5－6］，激光等离子体加速器［7－8］，高次谐波的产生［9－10］等.由于衍射效应，激光在等离子体中传播一个瑞利长度后就会发散，而在许多应用中要求激光在等离子体中传播几个甚至几十个瑞利长度.研究发现通过控制注入电子的相位，使其匹配激光传播，可以获得稳定的高能电子束，部分离化的等离子体也会影响激光的稳定传播，如P.Sprangle等［11］指出部分离化等离子中存在的离子和原子的相互作用对3阶相位的匹配很重要，而且部分离化等离子体中束缚电子作用会产生等离子体电子密度调制不稳定性［12］.

最近有研究表明，激光作用于等离子体中的自相位调制是产生激光自聚焦效应的原因之一［13－15］，而且激光作用于等离子体中的频率变化也与自相位调制(self－phasemodulation，SPM)密切相关［16－22］.基于这些研究，本文从激光在部分离化等离子体中传播方程出发，考虑了群速度色散(group velocity dispersion，GVD)、相对论SPM及非线性极化SPM的影响，推导出部分离化等离子体中激光焦斑半径和脉冲长度的演化方程，经过数值解析求解，分析了GVD和SPM对激光作用强弱的影响因素.

1 激光焦斑半径和脉冲宽度演化方程组

在部分离化等离子体中，取激光脉冲归一化矢势为

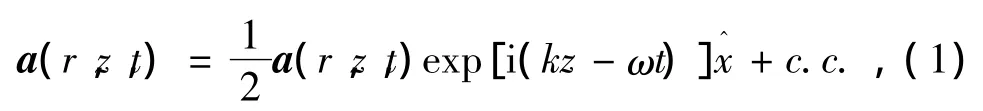
其中，假定激光脉冲是沿着z方向传播线偏振激光，k，w分别是激光的波数和频率归一化矢势 a=eA/mc2，取A为激光场矢势，e为单位电荷量，m为静止状态下电子质量，c为光速.

将等离子体极化强度矢量P及电流密度矢量J代入部分离化等离子体的波动方程，可得在库仑规范∇·a=0下，激光脉冲在部分离化等离子体中传播方程为［18－22］

其中，取r0＞L0＞λp，此时慢等离子体扰动被忽略，L0为起始脉冲宽度，λp为等离子体波长;kp=ωp/c为等离子体波数，wp为电磁场中等离子体振荡频率，R=Pa/Pp=8πχ(3)(mc/e)2ω4/ω2p为非线性极化强度，χ(3)为第3阶极化率，Pp为等离子体中的相对论激光临界功率，Pa为气体中非线性聚焦临界功率.(2)式为激光场的波动方程，右边第1项为真空衍射项和相对论非线性，而第2项为部分离化非线性效应.

取运动坐标系(z，ξ=z－βgct)，其中 βg=vg/c为标准化的脉冲群速度，代入色散关系ω2/c2－k2－kp+4πω2χ(1)/c2=0，a(r，z，ζ)为激光的缓变包络复振幅，则(2)式可变换为

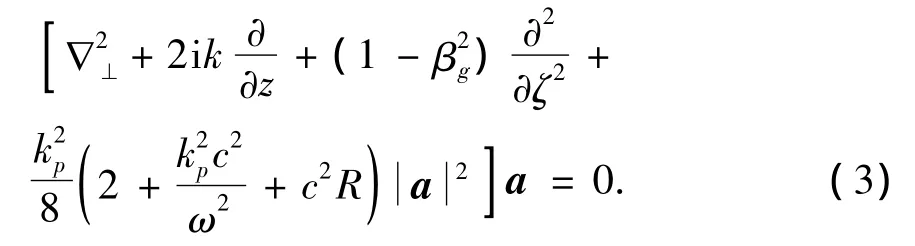
方程(3)可采用变分法来求解，其Lagrangian密度为［18］

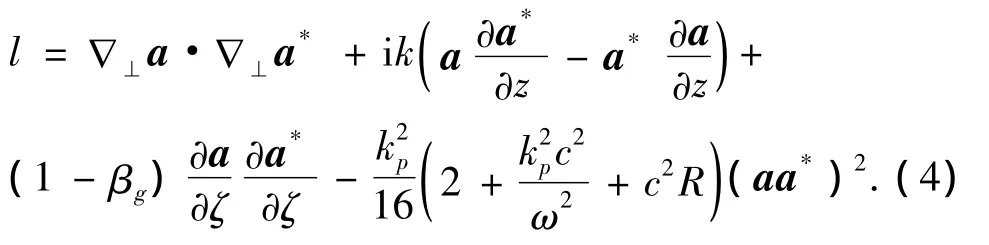
为了求解方程(3)式，取激光的径向分布与轴向分布都为高斯型，则缓变复振幅a(r，z，ζ)的试探函数可设为

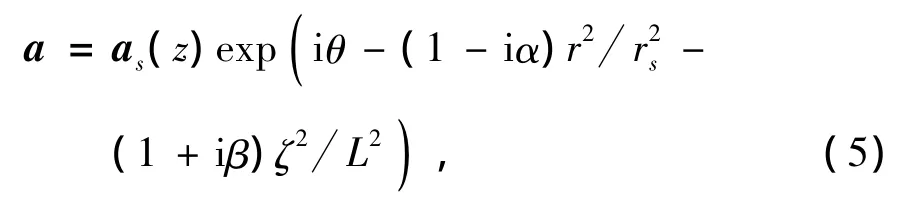
其中as(z)，θ(z)，α(z)，rs(z)，β(z)和L(z)分别为激光振幅，传播相移，波面曲率，焦斑半径，啁啾系数和脉冲宽度.将(5)式代入(4)式并通过可以推导出约化的Lagrangian密度，分别对β(z)，rs(z)，L(z)变分可以得［18］

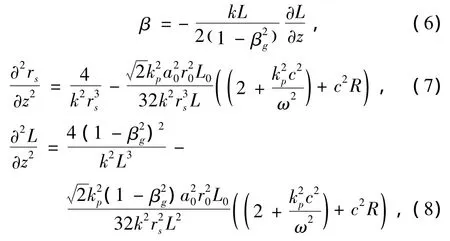
(6)式给出了啁啾系数β与脉宽L的关系方程;(7)式给出了焦斑半径在激光脉冲作用于部分离化等离子体中的演化方程;右边第1项为真空衍射，右边第2项为相对论作用，右边第3项为粒子自聚焦效应;(8)式给出了脉冲宽度在激光脉冲作用于部分离化等离子体中的演化方程;右边第1项为GVD，右边第2项为相对论效应SPM，右边第3项为非线性极化SPM.

激光的脉冲在部分离化等离子体中传播时的频率变化可由合相位φ给出:

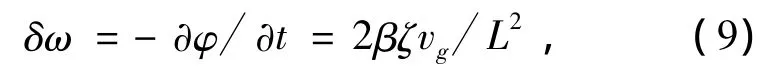
由(9)式可知，当β＞0时，激光脉冲为正向啁啾的，其频率在整个传播过程中是增长的;当β＜0时，激光脉冲为负向啁啾的，而频率在整个传播过程中是减小的;将(6)式代入(9)式可知频率的啁啾函数是与传播距离z与激光脉冲宽度L有关:

而又根据(8)式可知脉冲宽度L的变化是与GVD与SPM有关，所以群速度色散与自相位调制也对δω即频率的啁啾也有影响.

2 数值结果与讨论

现在可以通过微分方程(7)～(8)的解来描述强激光脉冲在部分离化等离子体中的传播特性，但由于该方程的高度非线性，求其解析解较为困难，可以通过4阶Runge－Kutta法进行数值求解.定义初始条件为和，激光和等离子体初始参数为:a0=0.04，r0=40 μm，L0=10 μm，R=100，其中a0为初始时激光强度，r0为初始时激光焦斑半径，L0为初始时激光脉冲宽度，R为初始时等离子体非线性极化强度(电离程度).在等离子体密度一定时，图1给出了GVD与SPM单独作用下，激光归一化焦斑半径rs/r0随归一化传播距离z/ZR的变化的演化关系，其中z/ZR为瑞利长度.从图1中可知，在部分离化等离子中，GVD使激光脉冲衍射发散，SPM使激光脉冲产生自聚焦;如图2所示，当等离子体密度变化时，给出了不同等离子体密度下，rs/r0和L/L0随z/ZR变化规律.由方程(7)～(8)可知rs及L的变化与GVD和SPM密切相关，其中包括相对论SPM及非线性极化SPM.当n0=0.005nc(nc为等离子体临界密度)时，SPM对激光脉冲作用小于GVD对激光脉冲作用，激光脉冲表现为衍射发散;当n0=0.01时，随着等离子体密度增大，SPM对激光脉冲作用增强，SPM对激光脉冲作用大于GVD对激光脉冲作用，激光脉冲表现为自聚焦效应.随着等离子体密度的增大，激光脉冲在部分离化等离子中传播的焦斑半径及脉冲宽度的自聚焦效应得到了有效的增强，而且随着等离子体密度的增大，激光自聚焦愈明显.

图1 等离子体密度一定，GVD与SPM单独作用下，激光归一化焦斑半径(rs/r0)随归一化传播距离(z/ZR)的变化规律

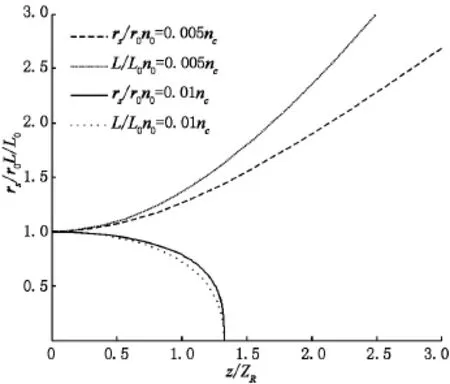
图2 在不同等离子体密度下，激光归一化焦斑半径(rs/r0)及归一化脉冲宽度(L/L0)随归一化传播距离(z/ZR)的变化规律

由(10)式可以确定激光脉冲在部分离化等离子体中传播频率变化与GVD和SPM的变化有关，根据图1结论可得图2在不同等离子体密度下，激光脉冲归一化频率变化δω/ω0随激光脉冲ζ/L的变化规律.n0=0.005nc时，激光脉冲发散，激光脉冲频率为负向啁啾变化，δω/ω随z/ZR增大而减小，表现为红移减小现象;n0=0.01nc时，激光脉冲聚焦，激光脉冲频率为正向啁啾变化，δω/ω随z/ZR增大而增大，表现为蓝移增大现象.因此，随着等离子体密度增大，激光频率由负向啁啾变化转变为正向啁啾频率变化，而且随着激光传播，激光脉冲红移减小而蓝移增大，见图3.

图3 在不同等离子体密度下，激光脉冲归一化频率变化(δω/ω0)随激光脉冲(ζ/L)的变化规律

3 结论

本文从有限长激光脉冲在部分离化等离子体中传播的激光场的波动方程出发，其中考虑了GVD和SPM的影响，通过分析激光脉冲焦斑半径和脉冲宽度满足的耦合方程及啁啾系数与脉冲宽度的关系方程，详细讨论了等离子体密度对激光传播特性的影响.在部分离化等离子体中，GVD作用于激光脉冲，发生衍射发散效应，SPM作用于激光脉冲，产生自聚焦效应;随着等离子体密度增大，SPM对激光脉冲作用增强，激光的自聚焦效应增强，并当n0=0.01时，可以明显的观察到激光的自聚焦效应;由(10)式可知，激光脉冲的传播频率变化，也与GVD和SPM有关，随着等离子体密度增大，激光频率由负向啁啾变化转变为正向啁啾频率变化，而且随着激光传播，激光脉冲红移减小而蓝移增大.值得说明的是，在部分离化等离子体中，激光脉冲的变化，不仅与GVD和SPM有关，尾波场效应对激光脉冲也有明显影响［7］.故通过研究激光在部分离化等离子体中传播特性可以进一步理解其物理机制，为以后实验研究提供理论指导.

［1］ MalkaV，Fritzler S，Lefebvre E，et al.Electron acceleration by a wake field forced by an intense ultrashort laser pulse［J］.Science，2002，298(5598):1596－1600.

［2］PukhovA，Meyer terVehn J.Laser wake field acceleration:the highly non－linear broken－wave regime ［J］.Appl－Phys B，2002，74(415):355－361.

［3］Mangles S P，Murphy C D，Najmudin Z，et al.Monoenergetic beams of relativistic electrons from intense laserplasma interactions［J］.Nature，2004，431(7008):535－542.

［4］Geddes C G，Toth C S，Van Tilborg J，et al.High－quality electron beams from a laser wakefield accelerator using plasma－channel guiding ［J］.Nature，2004，431(7008):538－578.

［5］Tabak M，Hammer J，Glinsky M E，et al.Ignition and high gain with ultrapowerful lasers［J］.Phys Plasmas，1994，1(5):1626.

［6］Lindl J.Development of the indirect－drive approach to inertial confinement fusion and the target physics basis for ignition and gain ［J］.Phys Plasmas，1995，2(11):3933－4024.

［7］ Zhang Shan，Xie Baisong，Hong Xueren，et al.Solitary waves of laser pulse in a plasma channel［J］.Phys Plasmas，2011，18(3):33104.

［8］Esarey E，Sprangle P，Krall J，et al.Laser wakefield acceleration and relativistic optical guiding［J］.IEEE Trans Plasma Sci，1996，24(2):252.

［9］RundquistA，Durfee C G，Chang Zhenghu，et al.Phasematched generation of coherent soft X rays［J］.Science，1998，280(5368):1412－1415.

［10］Milchberg H M，Durfee C G，McIlrath T J.High－order frequency conversion in the plasma waveguide［J］.Phys Rev Lett，1995，75(13):2494.

［11］Sprangle P，Esarey E，Hafizi B.Propagation and stability of intense laser pulses in partially stripped plasmas［J］.Phys Rev E，1997，56:5894.

［12］Durfee C G，RundquistA R，Backus S，et al.Phasematching of high－order harmonics in hollow waveguides ［J］.Phys Rev Lett，1999，83:2187.

［13］Ren C，Duda B J，Hemker R G，et al.Compressing and focusing a short laser pulse by a thin plasma lens［J］.Phys Rev E，2001，63:26411.

［14］Gordan D F，Hafizi B，Hubbard R F，et al.Asymmetric self－phasemodulation and compression of short laser pulses in plasma channels［J］.Phys Rev Lett，2003，90:215001.

［15］Shorokhov O，PukhovA，KostyukovI.Self－compression of laser pulses in plasm ［J］.Phys Rev Lett，2003，91:265002.

［16］Kosareva O G，Panov NA，Uryupina D S，et al.Optimization of a femtosecond pulse self－compression region along a filament in air［J］.Appl Phys B:Lasers Opt，2008，91:35.

［17］CouaironA，Chakraborty H，Gaarde M B，et al.From single－cycle self－compressed filaments to isolated attosecond pulses in noble gases［J］.Phys RevA，2008，77:53814.

［18］Pallavi J，Vijay S，KostyukovI.Self－focusing and compression of laser pulses in partially stripped plasma［J］.Phys Plasmas，2011，18:73105.

［19］Hu Qianglin，Liu Shibing，Ma Shanjun.Nonlinear polarization of partially stripped plasmas in intense laser field［J］.High Power laser and Particle Beams，2004，16(7):870.

［20］Liu Mingping，Zheng Zhi，Liu Shiqiang.Effects of relativistic and ponderomotive nonlinearities on an intense laser pulse propagation in a plasma channel［J］.Commun Theor Phys，2012，58:569.

［21］刘明萍，陶志鹏，钟西鹃，等.在激光尾场加速中电子密度和初始动量对自注入及加速的影响［J］.江西师范大学学报:自然科学版，2013，37(1):33－36.

［22］刘明萍，陶志鹏，陶向阳，等.自注入电子束的加速及其对激光尾场的影响［J］.江西师范大学学报:自然科学版，2014，38(1):74－77.