高维数据流的聚类离群点检测算法研究

程 艳，苗永春

(江西师范大学计算机信息工程学院，江西南昌330022)

0 引言

随着云计算、物联网及社交网络等技术的兴起，数据的类型和规模正在不断增长和积累，大数据时代已到来.半结构化和非结构化数据是大数据时代的重要数据类型组成部分［1］.除此之外，数据像从“池塘”变成“海洋”，不仅数据的量大，数据的维数也剧增，结构化数据的处理方式无法满足时代需求，因此数据流的离群点检测成为当代研究的热点.离群点检测［2－4］目的是试图捕获那些显著偏离多数模式的异常情况.可用来避免疾病扩散、网络入侵检测、信用卡恶意透支、贷款证明的审核等，这些用途正是大数据时代下离群点检测盛行的原因.

迄今为止，对传统的离群点检测算法的研究已经取得丰硕的研究成果，但将其运用到采用数据流环境的应用领域，离群点检测的效果难以达到用户满意.问题在于数据流的数据是按照时间序列到达，一旦流过处理节点就不可再现，而传统静态数据集离群点检测算法对数据要进行多次扫描，无法满足数据流一次扫描的条件.另外，数据流的数据动态变化的频率远远高于静态数据的更新频率，现有算法无法跟上数据流变化的速度，效率低.大数据时代数据流的维数比较高，已有算法对高维数据集检测离群点的结果并不理想.

针对上述存在的问题，本文提出一种高维数据流的聚类离群点检测(clustering－based outlier detection for high－dimensional data stream，CODHD－Stream)算法.该算法采用滑动窗口技术控制数据流，运用属性约简算法对高维数据流预处理和基于距离的信息熵过滤机制的K－means聚类算法挖掘离群点，最后实验表明，该算法在较大程度上提高了对高维数据流离群点检测的效率和精确度.

1 问题描述和相关定义

1.1 数据流离群点挖掘

数据流［2］是一种高速到来的实时、连续、有序、只能被读一遍或少数遍的记录构成的序列.数据流中的记录的类型可以是关系元组，也可以是一个对象实例.在实际应用中，记录的类型多指关系元组，则数据流是由关系元组构成的数据集，数据流的长度是所包含记录的个数.

在实际工程应用领域，交互的数据多为高维数据流，高维是指数据属性比较多.高维数据流形式化的描述为:设S为高维数据流集，S为n维空间，其属性为A1，A2，…，An，则记 S=A1×A2× … ×An.n维数据流记为 D={D1，D2，…，Dm}，数据项分别为T1，T2，…，Tm时刻到达，每个 Di，i=1，2，…，m 均为一个n维记录，用Di={ai1，ai2，…，ain}∈S表示，其中aij表示为(i=1，2，…，m，j=1，2，…，n)数据项Di在属性Aj上的值.

由于数据流是不可再现的，即数据只能按照产生的顺序访问一次或少数次［3］，数据流的动态变化特性要求算法数据流的预处理速度要不低于数据流的更新频率，且能利用有限的存储空间对“无限”的数据流进行处理［4］.本文采用的数据流离群点检测框架图如图1所示.

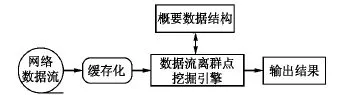
图1 数据流离群点检测框架图

数据流离群点检测算法可分为聚类、分类和频繁模式算法等.典型的聚类离群点检测算法包括K均值(K－means)、DBSCAN和CluStream聚类算法.K－means［5－6］算法和 DBSCAN［7］算法不能处理数据流中不同时间区间的聚类问题，另外该算法在处理高维数据流，一次完成数据处理，不仅运算量大，时间和空间复杂度也高.CluStream［8］算法利用界标窗口模型对数据流进行聚类分析，数据流的动态变化特性决定数据流中的微簇和离群点是可以相互转化的，而该算法不能适应滑动窗口下的聚类需求，且形成的微簇不能反映当前数据流中的数据分布状况.本文在借鉴上述K－means聚类算法的基础上，引入基于距离的信息熵过滤机制，提出了一种高维数据流的聚类离群点检测算法.

1.2 相关定义

定义1(属性的支持度p)属性集U={u1，u2，…，un}(n ≥ 1)，对应的关注度A={a1，a2，…，an}(0≤ai≤1，i=1，2，…，n)，则属性ui的支持度定义为

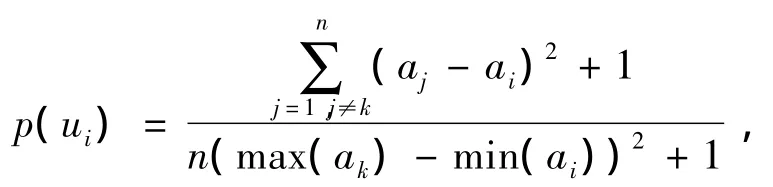
其中0≤p(ui)≤1，计算中对分母为0的情况进行消除，将式子分子、分母同时加1，避免接近于0的极其小的正数.

定义2(信息熵)对于有限集的随机变量X={x1，x2，…，xn}(n ≥ 1)，对应的概率为 p={p1，p2，…，pn}(0≤pi≤1，i=1，2，…，n)，且有1，则该有限集的信息熵为

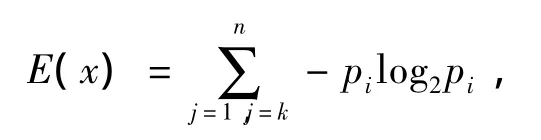
其中pi为发生事件xi的概率，n为可能发生的事件总数.

定义3(熵均值)对于有限集的随机变量X={x1，x2，…，xn}(n ≥ 1)，对应的信息熵值为 E={E(a1)，E(a2)，…，E(an)}，则该有限集的熵均值定义为

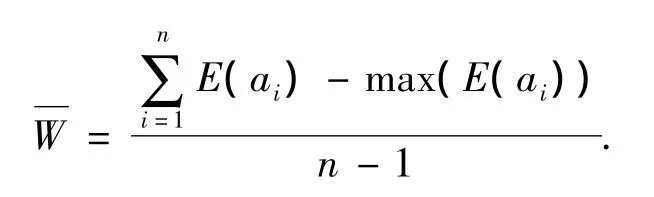
定义4(距离矩阵)KCoi和KCoj是微聚类KCo中的2个对象，则KCo的距离矩阵DM定义为

其中n为微聚类的对象数，m为对象的维数，dij是KCoi和KCoj之间的距离.

定义5(偏离度)微聚类中对象i的偏离度定义为

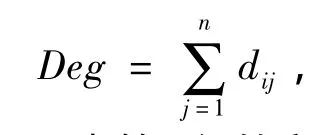
其中Deg为矩阵DM中第i行的和，对微簇类中的任意一个对象，都存在一个偏离度Deg，偏离度值越大，说明该对象与其他对象的距离越远，其为离群点的可能性越大.

2 高维数据流的聚类离群点检测(CODHD－Stream)算法

2.1 属性约简算法

针对实际应用，属性集中的属性存在核属性和非核属性之分［9］.其中，核属性是表述知识必不可少的属性，反之为非核属性.如果在数据挖掘前仅选取核属性参与运算，不仅可以排除非核属性带来的干扰，还可以大大降低算法的复杂度.

目前，数据降维方法［10－11］主要分为2类:线性降维和非线性降维，能够有效地对数据流进行特征提取，实现高维数据降维.如果采用这类降维方法，则CODHD－Stream算法必须2次遍历数据流.第1次遍历从数据中提取特征，输出数据集的特征空间，第2次遍历才可以根据提取到的特征空间，将数据投影到低维空间，再进行离群点检测.这种做法较难提高高维数据流的离群点检测的效率.一般针对实际应用，用户关注的数据的特征空间是有限的，只需要用户给出对数据项的各个属性的关注度T∈［0，1］，对不关注属性T取值为0，关注的属性，关注度T∈［0，1］，其中，决策属性的关注度为1.

算法1 属性约简算法

输入:m维数据流DS;数据项属性的关注度a1，a2，…，am

输出:核属性集CoreSet

(i)读数据流，移动滑动窗口界标，向前推n个元组;

(ii)根据用户给出对数据项属性的关注度A={a1，a2，…，an}，根据定义1计算出对应的属性支持度 P={p(a1)，p(a2)，…，p(an)};

(iii)根据定义2计算各维属性的信息熵概率E={E(a1)，E(a2)，…，E(an)}其中 E(a1)=log2p(ai);

(iv)删除最大的max(E(ai))，根据定义3计算属性组合的熵均值;

(v)判断属性的信息熵E(ai)是否大于属性组合的熵均值，若大于，则计算除去该属性后的信息熵E'(aA)－E(aA)=ε，若ε足够小，则i为核属性，反之，为非核属性;

(vi)返回核属性集CoreSet.

2.2 基于距离信息熵过滤机制的K－means离群点检测算法

根据定义2，聚类中的对象分布的信息熵E(x)，用来描述聚类中对象分布指数.信息熵的阈值设定为

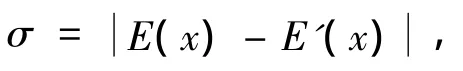
其中E'(x)为指每个聚类的信息熵，E(x)为去除偏离度最大的对象之后的微聚类的信息熵.比较对象排除前后信息熵变化，设定对应的一个阈值σ，如果σ变化无限小，几乎趋于0，则说明不包含离群点，从而把该微聚类过滤掉;反之，该对象是一个离群点，应该将其加入到离群点数据集中.

对于数据集A有m个数据项Ai组成Ai={ai1，ai2，…，ain}(i=1，2，…，m)，数据为 n 维.算法首先设定滑动窗口的大小为N，即滑动窗口内有N条n维的数据项A1，A2，…，An;然后将滑动窗口的数据流划分，顺序的m个数据点构成一个划分，采用属性约简算法对数据项降维，再对每个划分内的m个数据点进行k均值聚类.k均值聚类是一个改进的聚类算法.

算法2 基于距离信息熵过滤机制的K－means离群点检测算法

输入:m个数据点的数据集;

输出:k个离群点;

(i)将m个数据点的数据集初始化一个对应的簇m1，m2，…，mn和簇均值 Km1，Km2，…，Kmn;

(ii)计算任意2个聚类之间的距离，选择距离最小的2个聚类mi，mj，创建一个新的聚类mk和簇中心 Kmk，令mk={mi∪mj}，删除mi，mj即对应的簇中心Kmi，Kmj，并返回微聚类的个数c;

(iii)续处理下一个数据集划分中的m个数据点，根据簇中对象的均值，将m个数据点指派到最相似的簇中，更新每个聚类的簇均值;

(iv)反复执行，直至某一时段内的数据已全部遍历时，输出该数据集中微聚类的个数c和微聚类的中心;

(v)根据定义2计算聚类的信息熵，根据定义4得到相关的距离矩阵，根据定义5计算微聚类内对象的偏离度，并按降序排列;

(vi)从第1个对象开始依次取出，并计算余下数据集的信息熵值，判断该值是否小于阈值σ，若小于σ，则说明不包含离群点，排除掉此对象，否则取出该数据点，按照偏离度从大到小存至OSet离群点集合中;

(vii)输出OSet离群点集合前k个离群点.

2.3 CODHD－Stream算法思想

CODHD－Stream算法的主要思想是把滑动窗口的数据流按照到达的时间的先后顺序划分m个数据点，通过属性约简算法对数据集降维，得到核属性，即低维空间;把高维数据流中的数据项投影到该低维空间;用基于距离信息熵过滤机制的K－means算法检测数据集中的离群点，直至某时间段的数据流结束;最后输出OSet离群点集合前k个离群点.

3 算法性能与实验结果分析

3.1 算法理论分析

本文构造的CODHD－Stream算法具有良好的时间效率和精确度.由于属性集的约简可以排除不相关数据元素的干扰，便于针对特征空间划分微聚类，增加相似数据聚集度，从而提高算法的精确度.

定理1 CODHD－Stream算法具有相对于数据流数据集N线性的时间复杂度.

证滑动窗口的长为N，设数据的维数为m为常数，属性约简算法的复杂度O(m×N)，属性约简后的属性为m'为常数，最坏的情况下m'=m.离群点检测阶段，将数据集划分成微聚类，划分需要时间复杂度为O(2m'×N).最坏的情况下，划分成的微聚类的个数为N，算法检测微聚类的离群点需要O(m×N)，CODHD－Stream算法总共需要时间复杂度为O((2m'+m)×N)，因此，算法具有线性的时间复杂度.

实际情况下，由于高维数据流比较稀疏，属性约简后的维数远小于m，划分成的微聚类个数一定小于N，则CODHD－Stream算法对高维数据流进行离群点检测的效果较理想.

3.2 实验结果分析

为验证CODHD－Stream算法的效率及有效性，将通过实验类比较CODHD－Stream算法和CluStream算法各自的性能，通过实验对CODHD－Stream算法的检测精确度和效率进行分析.算法采用C++语言实现，硬件配置:CPU 2.6 GHz、内存1 GB、硬盘512 GB;开发工具:VS2010;所采用的实验数据是在基于Moodle网络教学平台采集的数据，本实验用到的数据记录来源于虚拟学习社区局域网防攻击行为模块所得的TCP、UDP连接记录.

由于采集到的数据量比较大，本实验选择最新的2600条记录，每个数据项有40个属性构成，包括登录的IP地址、登录时间、传输字节数、文件创建量、登录次数、失败登录次数等，给定属性的关注度分别为 1，0.98，0.97，0.87，0.88，0.90，….

本实验的精确度的评价标准是实际检测出离群点个数占数据集中包含离群点个数的比例，比例越大，精度越高.通过6次实验，取实验结果的平均值，实验结果如图2所示.

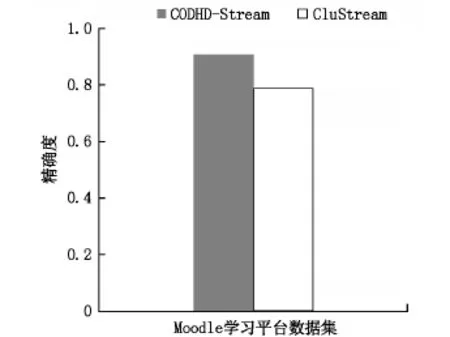
图2 2种算法的精度比较图

由图2可知，对于相同的数据集，CODHDStream算法的精度在90%左右，而CluStream算法的精度不到80%，采用改进的算法CODHD－Stream的离群点检测的精度更高.由于CODHD－Stream算法采用了属性约简算法对高维数据流进行降维处理，排除无用属性的干扰，因此该算法适合处理高维数据集.

处理数据集的执行时间是在单个局部站点进行的，所有结果均取自10次实验平均值，实验结果如图3所示.

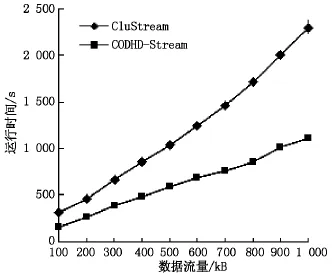
图3 2种算法的运行效率的比较图

从图3可以看到算法的处理时间都随数据流量的增加呈线性增长，变化趋势总体上保持一致，CODHD－Stream算法的处理时间明显大于CluStream算法.可见，CODHD－Stream算法时间复杂度比CluStream算法小，这是由于CODHD－Stream算法中的离群点检测算法是基于K－means和距离信息熵过滤机制挖掘离群点算法，该算法较大程度上降低了算法的时间复杂度.

为了测试数据维数对算法的影响，人工生成分别为15，20，25，30，35 维数的数据集，如图 4 所示，随着维数的增加，算法执行时间几乎呈线性增长趋势，说明该算法对高维数据流具有较好的伸缩性.

图4 维数对算法的影响图

4 结束语

本文在深入研究当前比较典型的数据流的聚类算法的基础上，提出了适合高维数据流的聚类算法，该算法首先设定合适的滑动窗口大小，对滑动窗口的数据流按顺序进行划分，对每段数据集先用属性约简算法进行预处理，再用基于K－means和距离信息熵过滤机制挖掘离群点算法进行离群点检测.该算法具有较快的处理速度，较高的精确度，能够满足高维数据流的离群点检测的要求.在下一步的工作中，笔者打算将本文提出高维数据流的聚类算法运用在智能网络教学的异常学习行为检测的领域中.

［1］ Wu Xindong，Zhu Xingquan，Wu Gongqing，et al.Datamining with big data ［J］.Knowledge and Data Engineering，2014，26(1):97－107.

［2］ Wang Changdong，Lai Jianghuang，Huang Dong，et al.SVStream:a support vector－based algorithm for clustering data streams［J］.IEEE Transactions on Knowledge and Data Engineering，2013，25(6):1410－1424.

［3］AlbaneseA，Pal S K，Petrosino，A.Rough sets，kernel set，and spatiotemporal outlier detection ［J］.Knowledge and Data Engineering，2014，26(1):194－207.

［4］Kollios G，Gunopulos D，Koudas N，et al.Efficient biased sampling for approximate clustering and outlier detection in large data sets［J］.Knowledge and Data Engineering，2003，15(5):1170－1187.

［5］Charalampidis D.Amodified k－means algorithm for circular invariant clustering［J］.PatternAnalysis and MachineIntelligence，2005，27(12):1856－1865.

［6］Kanungo Tapas，Mount D M，Netanyahu N S，et al.An efficient k－means clustering algorithm:analysis and implementation ［J］.PatternAnalysis and MachineIntelligence，2002，24(7):881－892.

［7］YipA M，Ding C，Chan T F.Dynamic cluster formation using level setmethods［J］.PatternAnalysis and MachineIntelligence，2006，28(6):877－889.

［8］ Guha S，MeyersonA，Mishra N，et al.Clustering data streams:Theory and practice［J］.Knowledge and Data Engineering，2003，15(3):515－528.

［9］Jiang Feng，Sui Yuefei，Cao Cungen.An information entropy－based approach to outlier detection in rough sets［J］.Expert SystAppl，2010，37(1):6338－6344.

［10］Kapoor R，Gupta R.Non－linear dimensionality reduction using fuzzy lattices［J］.IET ComputerVision，2013，7(3):201－208.

［11］Nie Bin，Wang Zhuo，Du Jianqiang，et al.The research for information granule reduction and cluster based on the partial least squares ［J］.Journal of Jiangxi NormalUniversity:Natural Science，2012，36(5):472－476.