Dirac方程的紧致分裂多辛格式

童 慧，孔令华，王 兰

(江西师范大学数学与信息科学学院，江西南昌 330022)

0 引言

自由粒子的运动在数学上可以用无量纲化的Dirac方程来描述.本文考虑Dirac方程的第1类初边值问题［1］:

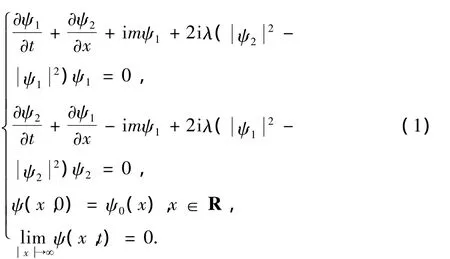
容易验证以上问题满足电荷守恒，即

上式是量子物理中的重要守恒律，数值方法对此守恒律的保持具有重要的意义和作用.对这一问题的数值方法的研究是近年来的热点问题［2-9］.

保持动力系统辛或多辛结构的数值格式在长时间数值模拟方面具有一定的优势，其重要构造方法之一就是Runge-Kutta方法，但是这种方法得到的多辛格式往往是完全隐式的.对于非线性问题需要求解非线性代数方程组［10］，应用起来非常消耗资源，效率比较低.而分裂步多辛算法很好地克服了这一弊端［11-15］.其基本思想是把原来的多辛哈密尔顿系统分裂成若干个辛或多辛哈密尔顿子系统，然后再对这些子系统构造辛或多辛算法.这一算法已经初步显示了它的优越性和高效的计算能力.为进一步提高计算效率和计算精度，在空间方向经常用具有高精度的能够保持辛结构的紧致格式离散.

多辛哈密尔顿系统的一般形式为

其中z∈Rm，M，K∈Rm×m是反对称矩阵，S(z)是光滑实函数，又称哈密尔顿能量泛函.它满足多辛守恒律:

其中微分形式ω =1/2d z∧M d z，κ=1/2d z∧K d z.

1 Dirac方程的多辛结构及其分裂子系统

Dirac方程(1)具有天然的多辛结构，即不需要引进正则动量就可以得到其多辛哈密尔顿系统的形式.为此令 ψj=pj+i qj，j=1，2;pj，qj为实函数，z=(q1，p1，q2，p2)T.把实部和虚部分开，得到相应的实函数方程

从而得到辛结构矩阵

哈密尔顿函数为

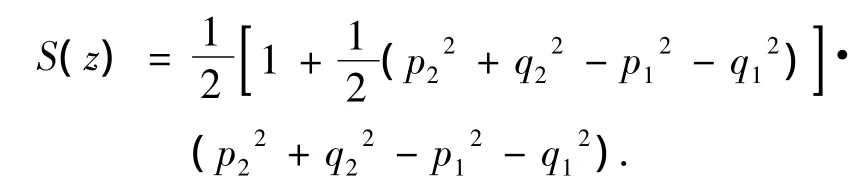
相应的多辛守恒律为

由S(z)的表达式可知，这是1个不可分的哈密尔顿系统，只能构造完全隐式的多辛格式.为了有效的求解方程(1)，可以利用分裂方法，将方程(1)分裂成线性子问题和非线性问题:

(2)式中的线性子系统具有与原系统一样的多辛结构，非线性子系统的辛结构为

易知非线性子系统具有点点的概率守恒:∀x，t，

这一点点守恒律将使得非线性子问题可以精确求解.用分离变量法计算可得其精确解为

2 辛Euler格式及分裂格式

利用平行线 xj=-L+jh(j=0，1，2，…，J)，tn=nτ(n=0，1，2，…，N)，剖分时空区域，其中h，τ分别是x与t方向的步长，用记号ψnj表示 ψ(x，t)在点(xj，tn)的近似.

2.1 空间的离散

在空间方向用高阶紧致格式去离散.考虑1阶导数fj'的x离散.运用文献［11］中的离散公式，有如下形式:

其中α，a1，b1都是待定参数，它们的数值由阶数的大小决定.

对上面的方程中各项在x=xj处作泰勒展开，可以得到方程组

选取α为自由参数，可解得a1=2(α+2)/3，b1=(4α-1)/3.此时的截断误差主项为 4(3α-1)f(5)h4/5!.若取 α =1/3，则 a1=14/9，b1=1/9，截断误差主项为4f(7)h6/7!.

把fx的离散格式写成线性算子的形式:

其中 R fj=(fj-1+3fj+fj+1)/3，I fj=(-fj-2-28fj-1+28fj+1+fj+2)/(36h).方程(3)对应的矩阵形式为

这里

注1 A是循环对称矩阵，B是循环反对称矩阵，从而A－1B是循环反对称矩阵，因而可以利用循环矩阵的有关性质计算它的特征值.

2.2 时间的离散

时间方向用辛Euler格式离散，即

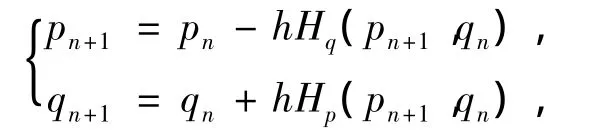
或

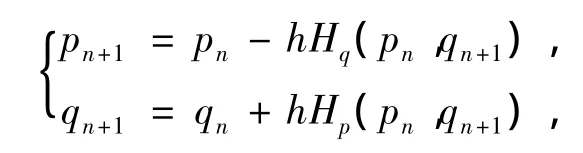
则非线性Dirac方程(2)的离散格式为

格式(4)中的前两式是对非线性子问题的精确求解，从而满足离散的辛守恒，而后两式是多辛格式.因而整个格式是辛格式，而且具有多辛格式的特征.

2.3 格式稳定性分析

这里讨论Dirac方程的紧致分裂多辛格式(4)的稳定性.非线性子问题是精确求解，而且解是稳定，因而对格式稳定性的研究只需要关注线性子问题的稳定性.为此令r=τ/h，D=hA-1B，则离散格式(4)的增长矩阵为

当增长矩阵的谱半径小于等于1时，格式稳定.考虑矩阵A，B的阶为N=2k.因为A，B是循环矩阵，利用循环矩阵的相关性质，可得它们的特征值分别为

而λN-j-2与λj共轭，这里的特征值都为实数，

而λN-j-2与λj共轭，且它们都是纯虚数.又因为A，B都是循环矩阵，则存在同一个正交矩阵Q，使得

即为h A-1B=D的特征值.按照上述对角线上特征值的排列顺序，将G的特征值依次记为 λ1(D)，λ2(D)，…，λN(D)，则矩阵G的特征方程为

当矩阵A，B的阶为奇数时，λ1(A)=5/3，λj(A)=1+(2/3)cos［2(j-1)π/N］，j=2，…，k+1.而 λN+2-j与 λj共轭..而 λN+2-j与 λj共轭.接下的讨论与上述类似.

3 数值实验

本部分考察Dirac方程的紧致分裂多辛格式的数值行为

其中

取Λ =0.75，根据初始条件，方程的孤立波解为

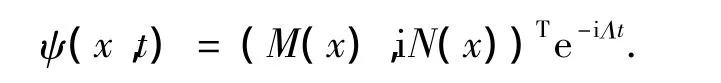
为了验证该数值方法的理论精度为O(τ+h6)，并且验证此格式比传统多辛格式在计算效率方面更具有优势.考虑x∈［-50，50］，取不同的h和τ计算，计算的最终时刻是T=1.表1和表2记录了数值模拟的结果，其中格式(a)为本文紧致分裂多辛格式，格式(b)为文献［9］中Lie-Trotter分裂的格式，格式(c)为文献［4］中2阶隐多辛龙格库塔格式.

表1 当τ=1×10-6时ψ1的误差、收敛阶、各个计算消耗的时间

表2 当h=0.1时ψ1的误差、收敛阶、各个计算消耗的时间

表1列出了当时间步长τ=1×10-6，空间网格点数N=100，200，400时在T=1时刻的数值解的误差和阶数，由此可验证该数值解在空间上以O(h6)逼近精确解，同时与文献［4，9］的格式对比，可以看出紧致分裂多辛格式(a)在空间精度上比格式(b)和格式(c)更高，运行时间也小于另外2种格式.

表2列出了当时刻T=1，空间步长h=0.1时采用不同的时间步长的数值解的误差和阶数，由此可以看出该数值解在时间上以O(τ)逼近精确解，与理论结果相符，并与另外2种算法进行比较，紧致分裂多辛格式的计算时间要少于另外2种格式的计算时间.

［1］ Alvarez A，Carreras B.Interaction dynamics for the solitary waves of a nonlinear Dirac model［J］.Phys Lett A，1981，86(6/7):327-332.

［2］ Alvarez A.Linear Crank-Nicholson scheme for nonlinear Dirac equations［J］.JComput Phys，1992，99(3):348-350.

［3］Alvarez A，Kuo P，L Vazquez.The numerical study of a nonlinear one-dimensional Dirac equation ［J］.Appl Math Comput，1983，13(1):1-15.

［4］Hong Jialin，LiChun.Multi-symplectic Runge-Kuttamethods for nonlinear Dirac equations ［J］.J Comput Phys，2006，211(2):448-472.

［5］Wang Han，Tang Huazhong.An efficient adaptivemesh redistribution method for a nonlinear Dirac equation［J］.J Comput Phys，2007，222(1):176-193.

［6］王健.Dirac方程的多辛格式［J］.上海交通大学学报:自然科学版，2004，38(5):849-852.

［7］周祖珍，李淮江.Dirac方程的对称性与守恒定律［J］.云南师范大学学报:自然科学版，1992，12(3):34-36.

［8］邵嗣烘，汤华中.非线性Dirac方程的数值研究［J］.高等学校计算数学学报，2005，27(S1):123-126.

［9］丁建，徐君祥，张福保.非周期 Dirac方程的稳态解［J］.中国科学:数学，2011，41(6):517-534.

［10］Wang Yushun，Hong Jialin.Multi-symplectic algorithms for Hamiltonian partial differential equations［J］.Commun Appl Math Comput，2013，27(2):163-230.

［11］Hong Jialin，Kong Linghua.Novelmultisymplectic integrators for nonlinear fourth-order Schrödinger equation with trapped term ［J］.Commun Comput Phys，2010，7(6):613-630.

［12］Kong Linghua，Cao Ying，Wang Lan.Split-step multisymplectic integrator for the fourth-order Schrödinger equation with cubic nonlinear term ［J］.Chin J Comput Phys，2011，28(1):76-82.

［13］王兰，符芳芳，童慧.Dirac方程的分裂步多辛格式［J］.江西师范大学学报:自然科学版，2013，37(5):462-465.

［14］王兰.多辛Preissmann格式及其应用［J］.江西师范大学学报:自然科学版，2009，33(1):42-46.

［15］黄红，王兰.薛定谔方程的局部1维多辛算法［J］.江西师范大学学报:自然科学版，2011，35(5):455-458.