某类高阶复微分方程解的增长性

龚 攀，肖丽鹏

(江西师范大学数学与信息科学学院，江西南昌 330022)

0 引言及主要结论

假定读者熟悉Nevanlinna理论中的基本结果和标准记号［1-4］，并用 ρ(f)表示复平面上亚纯函数f(z)的增长级，λ(f)和分别表示f的零点收敛指数和不同零点收敛指数，用λ2(f)和分别表示f(z)的2级零点收敛指数和2级不同零点收敛指数，ρ2(f)表示亚纯函数f(z)的超级，定义如下:

为进一步刻画解析函数在角域里的增长性，引入下面的定义.

定义1［5］设f(z)是角域={z:α ≤arg z≤ β，z＞0，0＜β-α≤2π}上非零解析函数，用ραβ(f)记做f(z)在上的级，其定义为

易知，若f是整函数，则在任一个角域内有ραβ(f)≤ ρ(f).特别地，如果在角域的增长级 ραβ(f)=+ ∞，则 ρ(f)=+ ∞.

定义2 设E⊂(0，+∞)上的可测集，用m(E)= ∫Ed t表示E的线性测度;对E⊂(1，+∞)，用ml(E)=∫Ed t/t表示E的对数测度;E(E⊂(1，∞))的上对数密度定义为

关于线性微分方程

其中A(z)和B(z)均为整函数.若A(z)为整函数，B(z)≢0为超越的整函数，f1，f2为方程(1)的2个线性无关解，则f1，f2至少有1个具有无穷级［6］.另一方面，方程(1)也可能存在有穷级解，例如f(z)=ez是方程f″+e-zf'-(e-z+1)f=0的有穷级解.一个自然的问题:当A(z)和B(z)满足什么条件时，能保证(1)式的每个解具有无穷级?很多学者研究了这个问题，参见文献［7-10］.

例如，在文献［8］中讨论微分方程f″+e-zf'+Q(z)f=0，并得到了如下一些结果.

定理A 假设Aj(z)(≢0)(j=0，1)是整函数满足ρ(Aj)＜ 1，a，b是复常数，且满足ab≠0和a=cb(c＞1)，则方程

的所有非零解为无穷级.

定理B 假设Aj(z)(≢0)，Dj(z)(j=0，1)是整函数满足ρ(Aj)＜ 1，ρ(Dj)＜ 1，a，b是复常数，并且ab≠0和arg a≠arg b或者a=cb(0＜c＜1)，则方程

的每个非零解为无穷级.

文献［11］讨论了微分方程f″+e-zf'(ez+1)+Q(z)f=0，当Q(z)满足某种条件时，可以保证方程每1个解具有无穷级.

本文考虑下列高阶线性微分方程

解的增长级，其中Q(z)为整函数，具有有限级，Pj(e-z)(j=1，2，…，k-1)为e-z的非常数多项式.易知方程(2)的每1个解均为整函数.下面考虑的问题是:当Q(z)具备什么条件时，可以保证方程(2)的每个非平凡解均具有无穷级?本文得到如下一些结果.

定理1 设Q(z)为超越整函数且具有有限级，Pj(e-z)(j=1，2，…，k-1)是e-z的非常数多项式.如果满足下列条件之一:

(ii)Q(z)=h(z)eaz，其中h(z)是非零整函数且级小于1，a∉R-的非零复常数，则方程(2)的每个非零解f具有无穷级.进一步在条件(ii)下有超级ρ2(f)=1.

定理2 假设Q(z)，Pj(e-z)满足定理1的条件，F(≢0)是有限级整函数，则方程(3)至多有1个可能的有限级例外解f0，其它的解f满足λ(f)=ρ(f)=∞.进一步，在定理1条件(ii)下有= λ2(f)= ρ2(f)=1.

1 主要引理

引理1［12］假设 f(z)是超越的亚纯函数且ρ(f(z))= ρ＜ ∞，H={(k1，j1)，(k2，j2)，…，(kq，jq)}是不同整数对的有限集合，满足ki＞ji≥0(i=1，2，…，q).∀ε ＞ 0，有下列结论成立:

(i)存在1个线性测度是零的集合E⊂［0，2π］，若 θ∈［0，2π］E，则存在常数R0=R0(θ)＞0，使得对所有满足arg z=θ和的z以及对所有(k，j)∈ H，有

(ii)存在1个对数测度有限的集合E⊂(1，∞)，使得对所有满足的z以及对所有(k，j)∈ H，有

(iii)存在1个线性测度有限的集合E⊂［0，∞)，使得对所有满足的z及对所有(k，j)∈H，有

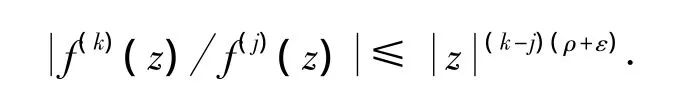
引理2［13］设g(r)和h(r)在(0，∞)上是单调的非减的实值函数，并且满足g(r)≤h(r)，r∉E，其中例外集的E对数测度有限.设α＞1，则存在1个常数r0＞0，使得g(r)≤h(αr)对所有r＞r0成立.

引理3［14］设A(z)(j=0，1，2，…，k-1)在角j域内解析，如果∀K ＞0及满足α＜θ＜β和

的θ具有一正测度，则方程f(k)+Ak-1f(k-1)+Ak-2f(k-2)+… +A0f=0的任意非零解都有

引理 4［8］假设 P(z)=(α +iβ)zn+ …(α，β是实数，是多项式且次数n≥1，A(z)(≠ 0)是整函数且 ρ(A)＜n，令 g(z)=A(z)ep(z)，z=r eiθ，δ(P，θ)= αcos nθ- βsin nθ，则对任意给定的ε ＞0，存在集合H1⊂［0，2π)，其线性测度为零，满足∀θ∈［0，2π)(H1∪ H2)，∃R ＞0，使得对，有

其中 H2={θ∈［0，2π);δ(P，θ)=0}是有限集.

引理5［15］ρ级(1/2≤ρ＜∞)整函数f(z)至少存在1个ρ级射线角域同时其每一ρ级射线角域的开度不小于πρ.

引理6［16］假设f(z)是1个级ρ(f)=ρ＜1/2的整函数，并且定义

若σ ＜ρ，则集合{r:m(r)＞rσ}有正的上对数密度.

引理 7［17］假设 A，A，…，A，F(≢ 0)，f满01k-1足微分方程f(k)+Ak-1f(k-1)+Ak-2f(k-2)+…+A0f=F且max{ρ(F)，ρ(Aj);j=0，1，…，k-1}＜ ρ(f)=ρ(0 ＜ ρ(f)≤ ∞)，则= λ(f)= ρ(f).

引理 8［18］设 A(j=0，1，…，k-1)是整函数j且满足 ρ(Aj)≤ ρ＜∞.若 f是微分方程 f(k)+Ak-1f(k-1)+… +A0f=0的解，则ρ2(f)≤ρ.

引理9［12］假设f(z)为亚纯函数，α＞1是1个给定的常数，则存在1个具有有穷对数测度的集合E⊂［1，+∞)，且存在常数B＞0仅依赖于α与(k，j)(k，j为整数且k＞j≥0)，使得对所有满足r∉ E 的点 z，有

2 定理的证明

定理1的证明 假设定理1满足条件(i)，由于ρ(Q(z))=λ≠1，下面分2种情况证明.

首先证明(Ⅰ)ρ(Q(z))=λ＞1.假设方程存在1个级为ρ(f)(＜∞)的非零解f，将得到矛盾.据引理1得，∀ε＞0，存在1个集合E⊂(1，∞)，其对数测度有限，使得对一切满足r∉E∪［0，1］的z及对所有(k，j)∈ H，有

成立，从而可得

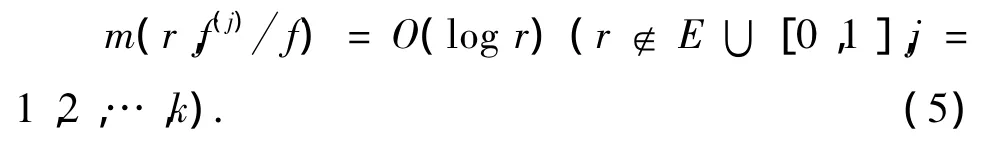
由方程(2)得

由(4)～(6)式可得

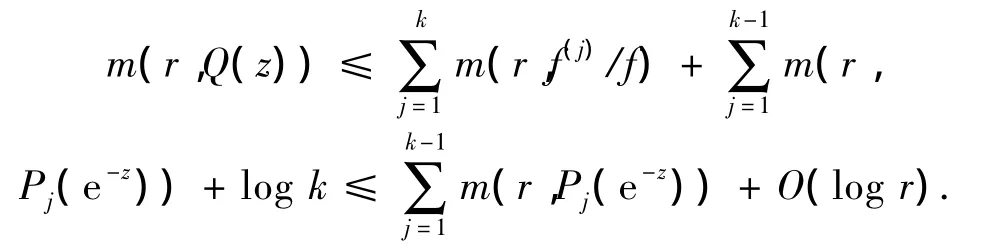
于是对所有的 r∉ E ∪［0，1］，有

设α ＞1，利用引理2，存在1个常数r0＞0，使得

对所有的r≥r0成立，由级的定义得ρ(Q(z))≤ρ(Pj(e-z))=1，这与ρ(Q(z))= λ ＞ 1矛盾.故得ρ(f)= ∞.

下面证明(Ⅱ)ρ(Q(z))=λ＜1.由于Q(z)是复平面上的超越整函数，以下分3种情形讨论.

情形1 当1/2≤ρ(Q(z))＜1，由引理5知存在角域Ω(α，β)β ≥ π/ρ(Q))，使得 ∀θ(α ＜ θ＜ β)，有

由于 ρ(Q)＜ ρ(Pj)=1，从而有πρ(Pj)＜πρ(Q).对Pj(e-z)来说，在复平面上对于正、负虚轴右半平面的角域有)，左半平面的角域有由于πρ(Q)＞ π，于是总存在角域 Ω(α'，β')，使得在此角域内满足(7)式.再根据引理3可知，对任何的常数K＞0，∃arg z=θ(α'≤ θ≤ β')，使得

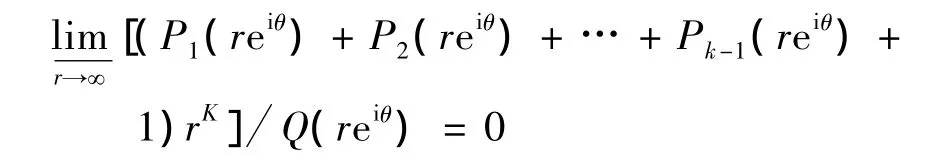
成立.于是可知对于方程(2)的任一非零解f，都有ρα'β'(f)= ∞.从而在整个复平面上有 ρ(f)= ∞.

情形2 当0＜ρ(Q(z))＜1/2时，应用引理6，存在一点列{rn}满足，使得对任意的角arg z= θ(θ∈［0，2π))，有

类似于情形1的证明方法可得矛盾.于是对方程(2)的任一非零解f，均有ρ(f)=∞.

情形3 当ρ(Q(z))=0时，由于Q(z)是1个超越的整函数，容易得到对于任意的角arg z=θ(0≤θ＜ 2π)，有

类似情形1的证明方法同样可得矛盾.于是对方程(2)的任一非零解f，均有ρ(f)=∞.因而情形(i)的结论成立.

下面证明定理1满足条件(ii)Q(z)=h(z)eaz.

令 a= α +iβ，α，β 是实数，z=r eiθ，则 δ(az，θ)=αcosθ- βsin θ.

下面证明断言:使得δ(az，θ)＞0的θ角域存在且和复平面上的右半平面有交集，并且交集具有正测度.设其交集为E，分3种情况讨论.

情形1 若 α =0，β ≠ 0，则 δ(az，θ)=- β·sin θ，当β ＞ 0时，sinθ＜ 0，取E=(- π/2，0)，则m(E)＞0;当 β ＜ 0时，sinθ＞ 0，取E=(0，π/2)，则m(E)＞0.

情形2 若α≠0，β =0，则δ(az，θ)= αcosθ，因为a∉R-的非零复常数，即α∉R-，则cosθ＞0.

类似情形1，可知断言成立.

于是，∀K ＞ 0，有

由引理3可知，对于方程(2)的任一非零解f，都有 ρφ1φ2(f)= ∞.也就是说在整个复平面 上有ρ(f)= ∞.

下证超级ρ2(f)=1.

根据引理8 可得 ρ2(f)≤ max{ρ(Pj)，j=1，2，…，k-1}=1.由(ii)中的断言，现在考虑角域Ω=(φ1，φ2)，在此角域内具有(8)式成立.

另一方面，由引理9可知，存在1个集合E1⊂［1，+∞)具有有穷对数测度和常数B＞0，使得当且r充分大时，有

又由(6)式和(9)式在角域Ω =(φ1，φ2)内，有

由(8)式和(10)式得

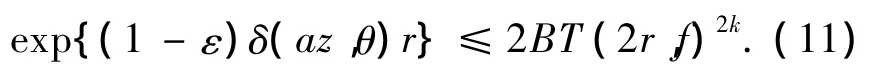
对(11)式取2次对数再除以log r，则ρ2(f)≥1.所以ρ2(f)=1.从而(ii)得证.

综上所述定理1得证.

定理2的证明 假设f0是方程(3)的有限级解，如果方程还有另外1个有限级解f1(≠f0)，则ρ(f1-f0)＜∞，且f1-f0为方程(2)的解，由定理1知，ρ(f1-f0)=∞，所以矛盾.故方程(3)至多有1个可能的有限级例外解f0.现在假设f为(3)的无穷级解，应用引理7，可得f满足∞.进一步的情形可类似证明，定理2得证.

［1］杨乐.值分布论及其新研究［M］.北京:科学出版社，1982.

［2］张广厚.整函数与亚纯函数理论:亏值，渐进值和奇异方向［M］.北京:科学出版社，1986.

［3］Hayman W.Meromorphic function［M］.Oxford:Clarendon Press，1964.

［4］Laine I.Nevanlinna theory and complex differential equations［M］.Berlin:W de Gruyter，1993.

［5］Wu Shengjian.On the growth of solutions of second order linear differential equations in an angle ［J］.Complex Variables，1994，24(3/4):241-248.

［6］Hille E.Ordinary differential equations in the complex domain［M］.New York:Wiley，1976.

［7］Hellenstein S，Miles J，Rossi J.On the growth of solutions of f″+gf'+hf=0 ［J］.Trans Amer Math Soc，1991，324(2):693-706.

［8］陈宗煊.微分方程f″+e-zf'+Q(z)f=0解的增长性［J］.中国科学:A 辑，2001，31(9):775-784.

［9］刘旭强，易才凤.关于2阶线性微分方程f″+Af'+B=0解的增长性［J］.江西师范大学学报:自然科学版，2013，37(2):171-174.

［10］李延玲，刘慧芳，冯斌.微分方程 f″+A1(z)eaznf'+A0(z)eaznf=F(z)的复振荡［J］.江西师范大学学报:自然科学版，2012，36(6):579-583.

［11］陶磊，龙见仁，伍鹏程.关于微分方程f″+e-z(ez+1)f'+Q(z)f=0解的增长性［J］.贵州师范大学学报:自然科学版，2013，31(2):46-49.

［12］Gundersen G G.Estimates for the logarithmic derivative of ameromorphic function，plus similar estimates［J］.JLondon Math Soc，1988，37(2):88-104.

［13］Bank S.A general theorem concerning the growth of solutions of first order algebraic differential equations［J］.Composition Math，1972，25(1):61-70.

［14］徐俊峰，仪洪勋.高阶线性微分方程解的角域增长性［J］.系统科学与数学，2008，28(6):702-708.

［15］戴宗基，嵇善瑜.ρ级射线及其Borel方向分布间的关系［J］.上海师范大学学报:自然科学版，1982(2):16-24.

［16］Barry P.Some theorems related to the cosπρtheorem［J］.Proc London Math Soc，1970，21(3):334-360.

［17］Chen Zongxuan，Gao Shian.On the complex oscillation of non-homogeneous linear differential equations with meromorphic coefficients［J］.Kodai Math J，1992，15(1):66-78.

［18］Chen Zongxuan.On the hyper order of solutions of higher order differential equations ［J］.Chin Ann Math，2003，24B(4):501-508.