基于逆最优问题的最优制导律及特性分析①

王 辉，王 江，郭 涛，王广帅

(1．北京理工大学宇航学院，北京 100081;2．北京航天自动控制研究所，北京 100854)

0 引言

随着智能弹药及精确制导技术的快速发展，很多攻击任务不仅要求精确命中，还对弹道末段的速度矢量角、攻角等提出了附加约束，如对装甲目标的越顶攻击、对坚固掩体内目标的侵彻攻击等，这均对精确导引技术提出了新的要求。

实际上，根据不同的任务需求，相关学者一直在研究各种具有针对性的制导律，并不断探索新的制导律。其中，能量最优制导律吸引的关注最多，工程应用也最广泛［1－3］。比例导引和弹道成型可认为是能量最优制导律的典型代表，相关研究也最深入［1－6］。比例导引的种类较多，如经典比例导引、增强型比例导引［1－3］、分段式比例导引［7－8］等。弹道成型制导律的概念最早由Zarchan提出［1］，其提出的制导律也被称为经典弹道成型制导律。在Zarchan工作基础上，Ben-Asher，Yaesh，Ryoo等对弹道成型的制导特性、剩余飞行时间(time-to-go)估算方法等进行了深入研究［5－6，9－10］。传统的能量最优制导律大都基于线性二次型最优控制理论，以控制量的平方的积分最小为目标函数，权函数取为常值1［1－2］。2006 年，Ryoo 和 Ohlmeyer等在研究角度控制问题时，引入导弹剩余飞行时间的幂函数，实现了弹道成型制导律的扩展，拓展了与此相关的制导律的研究范围［4－5，10］。

本文在典型的能量最优制导律基础上，创新性地将制导律的2个特征根从有限的点/线扩展到几乎所有的正实根，提出了制导律的逆最优问题，阐述了逆最优制导律中性能指标加权矩阵的构造、求解过程，并对不同特征根下的逆最优制导律的制导特性进行了系统研究。

1 能量最优制导律的常规形式

对地面静止或慢速移动目标，导弹和目标的几何关系如图1所示，OXY表示地面坐标系，M0表示导弹初始位置，LOS表示当前弹目视线(line of sight)，LOS0表示初始弹目视线，LOSf表示终端攻击时刻的弹目连线，(xt，yt)表示目标位置。图1中主要符号定义如表1所示，所有的角度定义逆时针为正，顺时针为负。

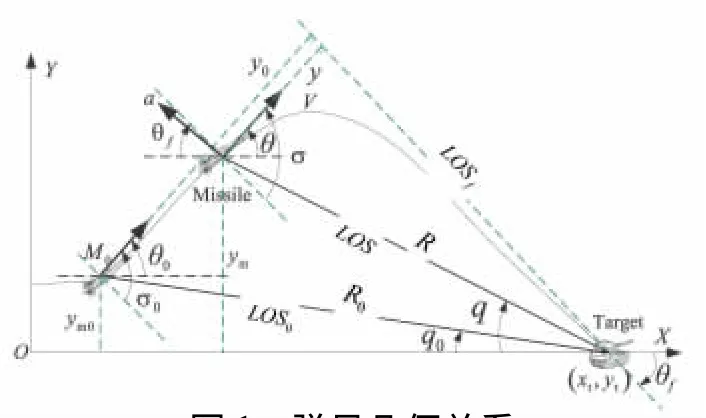
图1 弹目几何关系Fig．1 Geometry of the missile and target

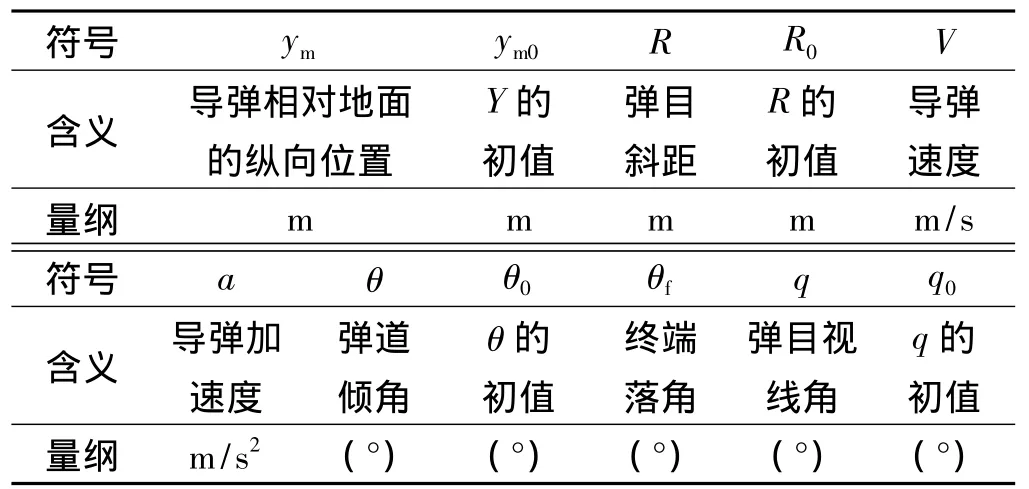
表1 主要符号定义Table 1 Definition of the main symbols

为便于后续的表述和推导，定义相对于终端弹目连线的纵向位置y和速度矢量角σ，初值分别为y0、σ0。由定义可知，σ、θ、θf的关系为

纵向位置 Y、y 与 θf、q 的关系为

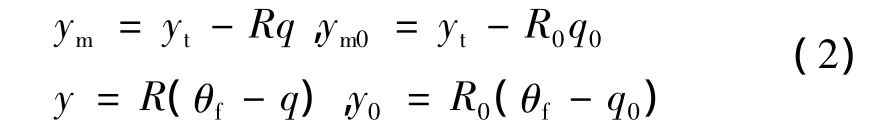
根据图1所示的弹目几何关系，建立如下的运动方程:

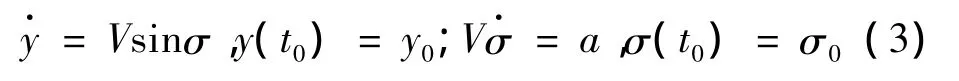
当忽略驾驶仪动力学时，导弹的加速度指令等于加速度响应，即u(t)=a，u为控制量。为了对式(3)进行线性化，假设V是常值、σ为小角，这也是研究线性最优制导律的2个常用假设［1－2］。这样，经线性化后，式(3)可表示为

其中，v=Vσ表示垂直于终端弹目连线的速度分量。

将式(4)写成矩阵的形式:

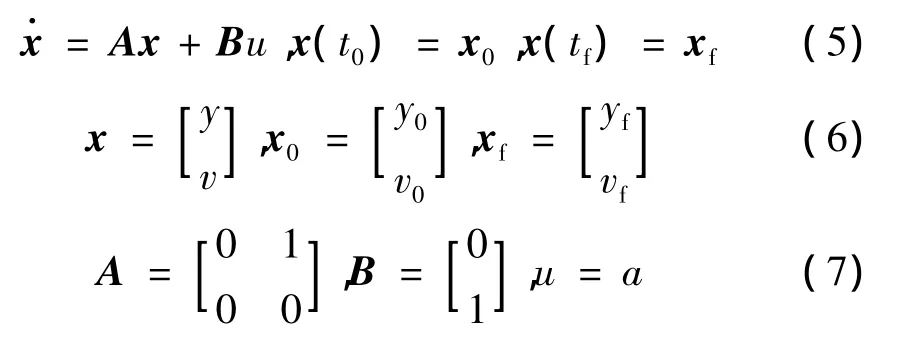
式中 tf为导弹制导时间;x0为状态初值;xf为状态终值。

根据式(5)～式(7)和最优控制理论，设定不同形式的权函数和目标函数，在不同的终端状态约束下，则可得到不同的能量最优制导律。如仅约束终端位置yf=0，不考虑终端约束权函数和状态权函数，控制权函数 R设为1，则得到传统的比例导引制导律(CPNGL，classic proportional navigation guidance law)，权函数R设为1/(tf－t)n，n≥0，则得到扩展的比例导引律(EPNGL，extended proportional navigation guidance law);若同时约束yf=0，vf=0，则可分别得到传统的/扩展的带落角约束的最优制导律(COGLIAC/EOGLIAC，classic optimal guidance law with impact angle constraint/extended optimal guidance law with impact angle constraint)。

表 2 给出了几种典型的能量最优制导律［1－2，4－5］。表2中，tgo=tf－t，表示导弹剩余飞行时间。对表2中带落角约束的制导律，由于文中定义了相对于终端弹目连线的角度σ，终端角度约束θf隐式包含于制导律中;若将式(1)及线性化的式(2)带入制导律中，则制导律可变换为直接含有终端角度约束θf的常规形式［1，4－6］。

2 逆最优制导律的提出及其加权矩阵的构造

2．1 最优制导律的扩展及其逆最优问题

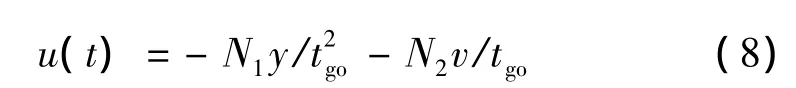
表示成矩阵的形式:

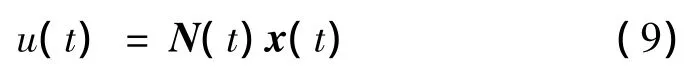
其中，N(t)为线性时变的制导增益矩阵，即

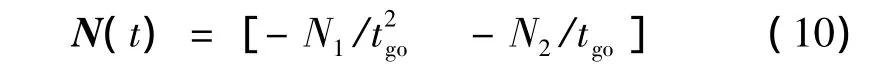
表2 典型的能量最优制导律Table 2 Typical energy optimal guidance laws

进一步，将式(8)表示成相对于地面坐标系的微分方程形式，有

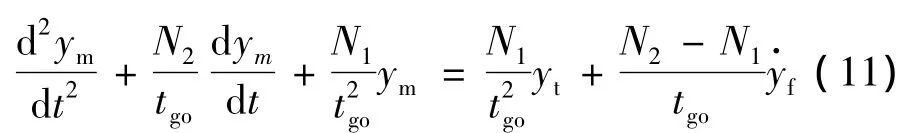
由式(11)可看出，制导律是否含有终端角度约束取决于N1、N2取值，当N1=N2时(如PN)，则制导律自然地不包含终端角度约束。

令y=tgoλ，则式(8)可写为 λ2－(N2+1)λ +N1=1，不妨再令方程的两实根分别为 λ1、λ2(λ1＞ λ2)，则N1=λ1λ2，N2=λ1+λ2－1，此时式(8)又可表示成:

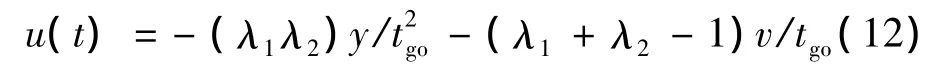
因 N1＞0，N2＞0，故 λ1λ2＞0，λ1+λ2－1 ＞ 0，即λ1＞0，λ2＞0，λ1+λ2＞1。根据表1中导航系数，容易得到典型最优制导律特征根(Characteristic roots，CR)λ1、λ2间的对应关系，如图2所示，其中阴影区表示逆最优制导律可能的特征根区域。

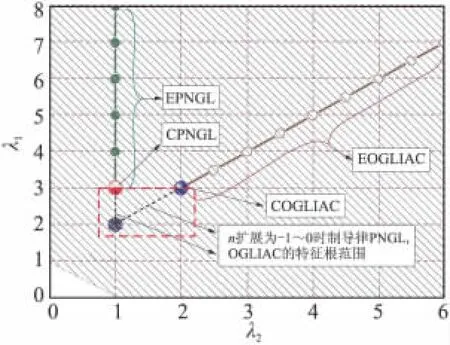
图2 典型最优制导律的特征根Fig．2 CR of the typical energy optimal guidance laws

在图2中，前述几种典型最优制导律的特征根只占据了有限的点/线区域，而提出的逆最优制导律极大地扩展了可能的特征根范围。现在的重点是能否找到合适的目标函数J，使最优制导律的形式满足式(9)，这就是最优制导律中的逆最优问题［10］。相应的，式(8)或式(12)称为逆最优制导律。

2．2 逆最优制导问题中加权矩阵的构造

为便于推导，将式(5)的状态方程和式(9)的控制方程统一写成如下形式:

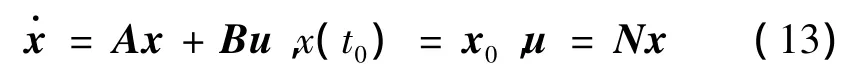
式中 x为m×1维向量;u为控制量，由式(5)的标量扩展为n×1维向量。

目标函数J设为

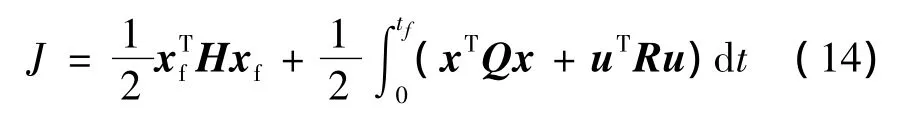
式中 H为终端约束权矩阵;Q为状态权矩阵;R为控制权矩阵;H、Q、R均为对称矩阵。

对由方程(13)构成的线性闭环制导系统，逆最优问题就是找到矩阵A、B、N所需满足的充分必要条件，确定矩阵H、Q和R并使式(14)的性能指标最小［10－11］。

对式(13)所示的最优控制问题，其直接的最优解N可由Riccati微分方程得到，即

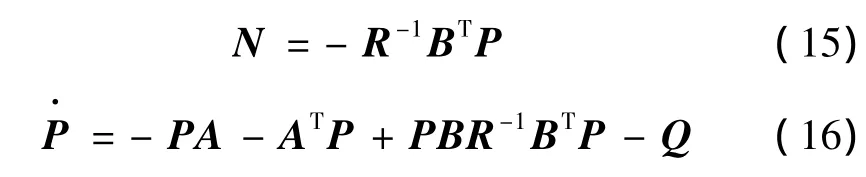
式中 P为对称矩阵。

式(16)的边界条件为

为了使方程(16)的解P(t)存在并唯一，传统的结论是要求H≥0，Q≥0，R ＞0，但文献［10－11］指出，对方程(13)～(14)所示的系统，当满足一定条件时，Q≥0并不是必需的。

不加证明，给出定理1:对方程(13)所示的线性闭环系统，矩阵B、N在区间［t0，tf］上可微并具有确定的常量秩，则可构造如式(14)所示的性能指标函数，其中矩阵H、Q、R满足如下条件:

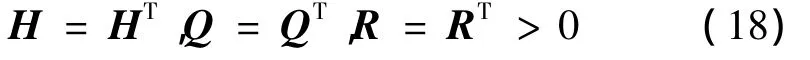
对区间［t0，tf］上的任意时间t及任意初值x0，如果矩阵NB具有n个线性独立的实特征向量且所有的特征向量均非正，且矩阵B、N的秩满足:

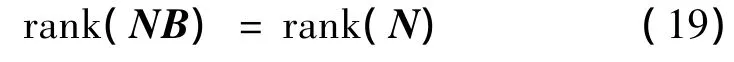
则能保证性能指标J的最小值J*≥0;

若矩阵B、N的秩满足式(20):

则能保证J*＞0。

假设定理1条件都满足，则可构造性能指标函数J的具体形式。首先构造矩阵R=RT＞0使矩阵RNB是对称的。已经知道矩阵NB的特征向量是线性独立的实向量，设矩阵V的列由BTNT的特征向量组成，则有如下表达式:

式中 U为BTNT特征值构成的对角阵。

这样，有定理2:假设矩阵NB具有n个线性独立的实特征向量，对由式(22)给定的实矩阵R=RT＞0可使矩阵RNB是对称的，即

其中，矩阵V的列选自矩阵BTNT的特征向量。

下面根据式(15)的结果来求解对称矩阵P:

设W为满足下列等式的任意n×m实矩阵，则

对比式(23)和式(24)可看出，－WTRN是式(23)中关于P的解，但－WTRN并不能保证P是对称的。为了得到对称的解，令

在式(25)两边同时左乘BT，得到

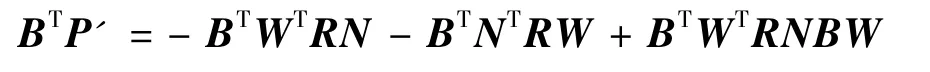
根据式(24)的结论，上式可简写为

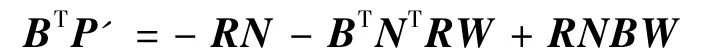
又由于矩阵R=RT，(RNB)T=BTNTR=RNB，则上式可进一步简化为

假设P是式(23)的任意实对称矩阵解，联立式(23)和式(26)，有

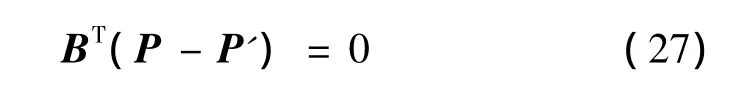
据此，可得式(15)的实对称矩阵解P:

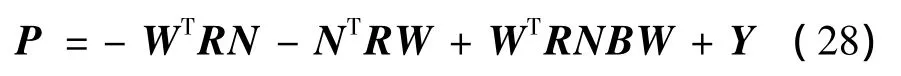
其中，Y为任意的实矩阵，满足如下条件

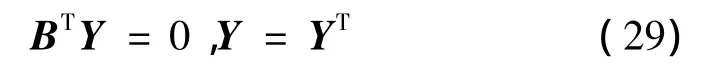
当矩阵NB的秩满足式(19)的条件时，关于矩阵P有定理3:令矩阵R是实对称的正定矩阵，RNB是对称矩阵，如果rank(NB)=rank(N)，则满足式(23)的实对称矩阵P可由给定的矩阵R表示:

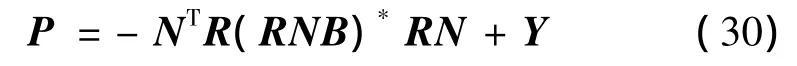
其中，矩阵Y满足式(29)，符号*表示矩阵的Moore-Penrose广义逆。

此外，矩阵H由H=P(tf)得到，矩阵Q由式(31)得到:

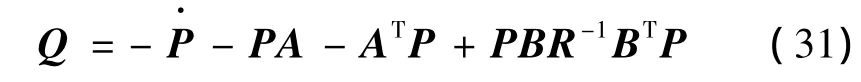
3 逆最优制导律中加权矩阵的求解

3．1 逆最优制导律对应的加权矩阵求解

对由式(5)～式(7)和式(9)构成的单输入闭环制导系统，由于rank(NB)=rank(N)=rank(B)=1且矩阵NB的特征向量非正，满足定理1的条件。由定理1中式(18)知，在性能指标函数J中，矩阵H、Q可设为对称的，矩阵R设为正的线性时变的标量R(t)。由于NB也是标量，由定理2知，每一个正的R(t)都能保证RNB是对称的。根据式(29)可知，矩阵Y是对称阵，且BTY=0，设矩阵Y的形式为

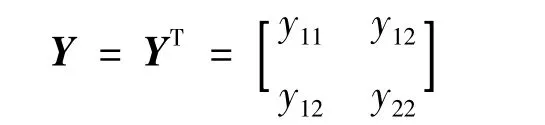
将Y带入BTY=0中，有

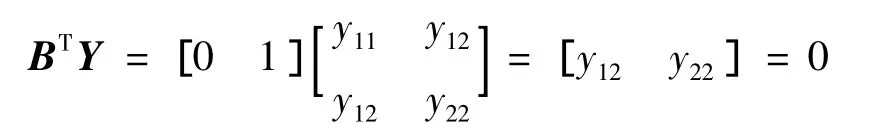
上式表明y12=y22=0，则矩阵Y可表示为

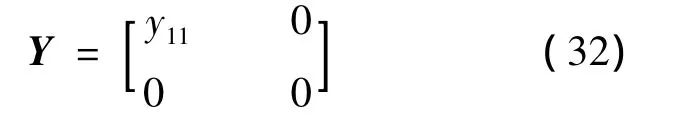
其中，y11为任意实数。

对任意给定的R(t)，定理3给出了实对称矩阵P的解。将矩阵Y、N、B以及标量R(t)带入式(30)中，求得矩阵P:

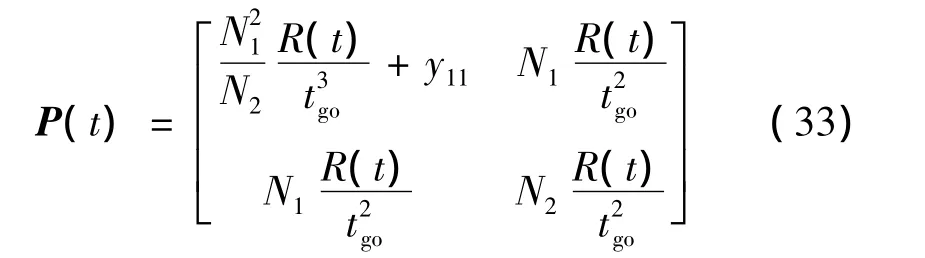
由于性能指标J*对所有的初值x0和t0都大于0，因此矩阵P也应为正定的，故要求y11＞0。为后续推导的方便，观察式(33)，不妨令

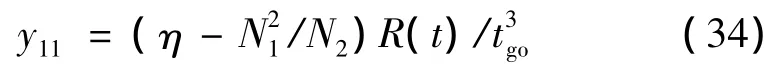
这样，矩阵P又可表示为

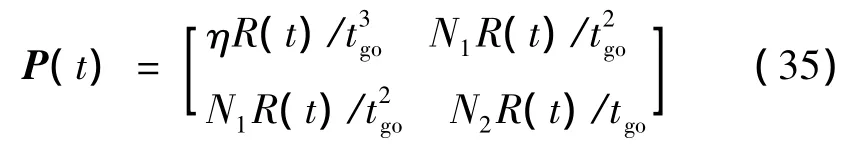
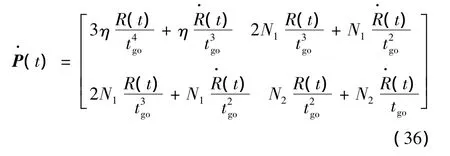
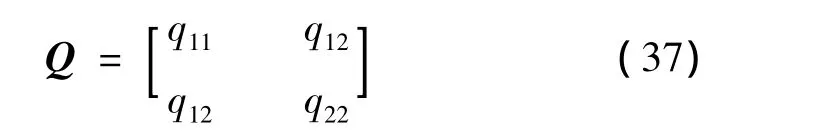
其中，Q的3个元素分别为

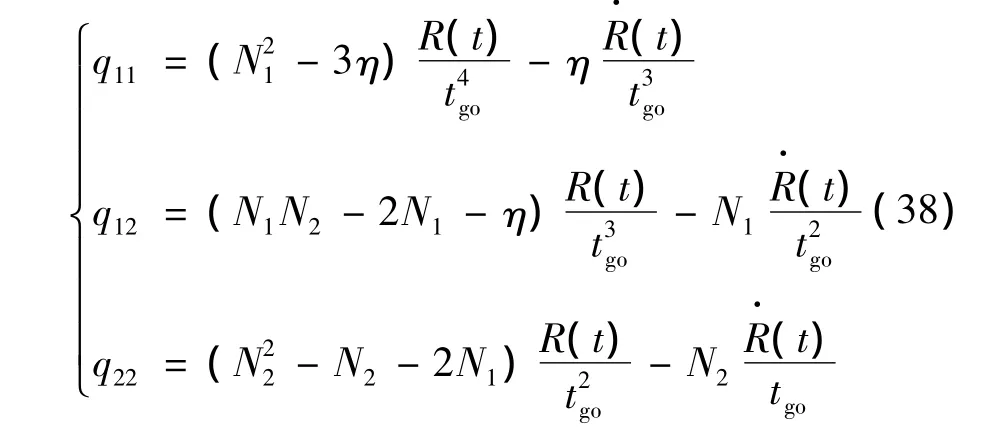
由于H=P(tf)，式(35)～式(38)即完成了逆最优问题中加权矩阵的构造。根据式(35)～式(38)，通过选取不同的η和R(t)，则可得到多组不同的［H，Q，R］。

3．2 加权矩阵求解的举例说明

下面对上述结果举例说明。不妨将R(t)取为表2中的形式，即

考虑矩阵Q的一种简单情况，即Q为对角阵，则式(38)中q12=0。将上式的R(t)带入q12，得

求解得

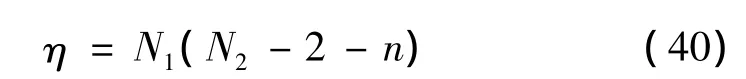
同时，η还需满足条件η＞N21/N2，亦即

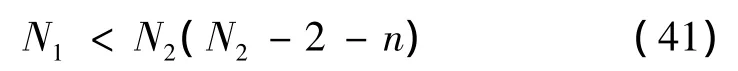
此时，矩阵P、Q分别为

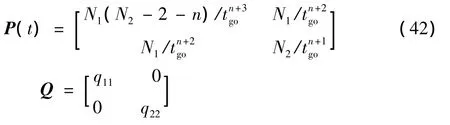
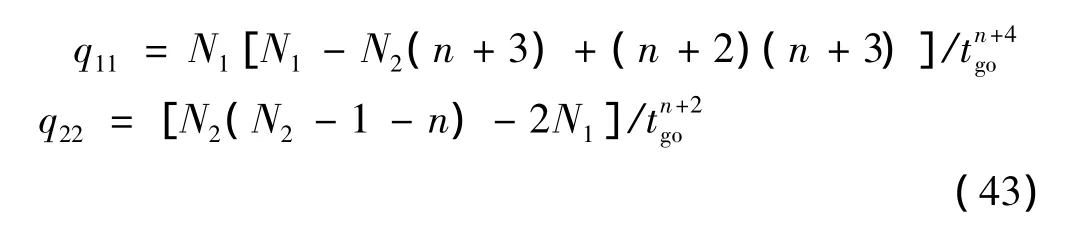
由式(43)可看出，若进一步使Q=0，则相当于在性能指标式(14)中不考虑状态约束。令式(43)中q11=q22=0，求得 N1、N2的值为

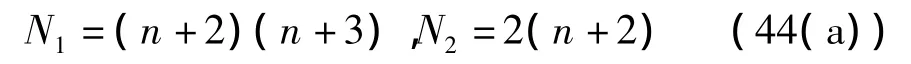
或

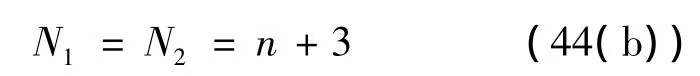
对比表2中的表达式可知，式(44(a))、式(44(b))的导航系数分别对应EPNGL和EOGLIAC两种制导律，此时，与式(44(a))、式(44(b))对应的矩阵P分别为

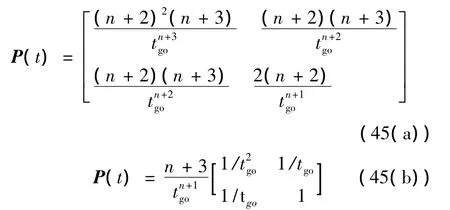
观察式(45(a))、式(45(b))可看出，只要 n＞－1，在末段时刻 tf处，P→∞;又由于 H=P(tf)，则 H可表示为

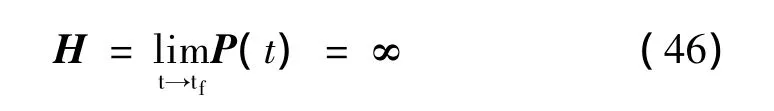
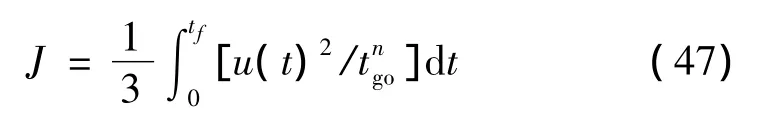
由前述的推导和分析可看出，对式(8)所述的制导律，通过选取合适的η和R(t)，任意大于零的导航系数N1、N2都可能是特定条件下的最优结果。这样，通过制导律中逆最优问题的研究，再次拓展了最优制导律的内涵。

4 不同特征根下的制导律制导特性分析

4．1 特征根选择

根据式(11)及 N1=λ1λ2，N2=λ1+λ2－1，相对地面坐标系的逆最优制导律可表示为

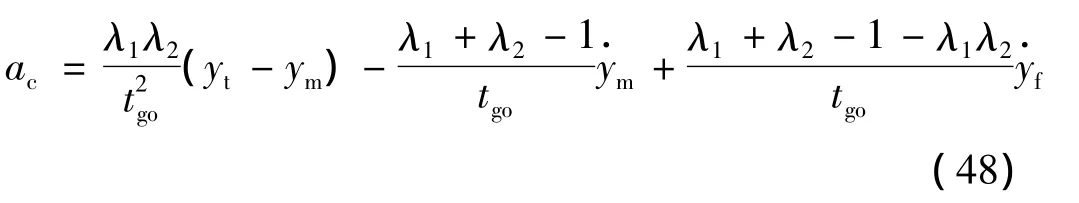
可进一步表示成以导引头敏感的弹目视线角q、弹目视线角速率的形式:

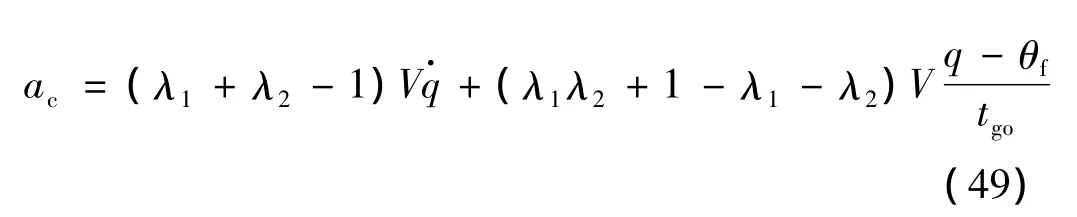
其中，ac为加速度指令。

根据式(44)的结果，容易计算得到EPNGL和EOGLIAC对应的特征根分别为λ1=n+3，λ2=1和λ1=n+3，λ2=n+2。

为研究不同特征根下的制导特性，并使研究具有代表性，特征根的选取如表3所示。其中，③、⑥分别对应EPNGL和EOGLIAC。

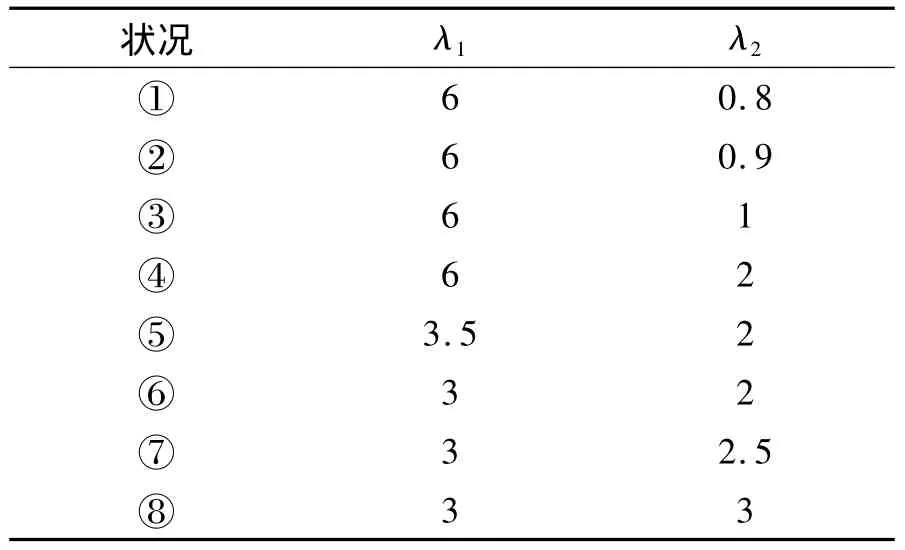
表3 选取的典型特征根Table 3 Chosen value of CR

4．2 制导特性对比分析

引入一阶驾驶仪动力学1/(Tgs+1)，研究制导律在特征根变化时(如表1所示)的制导特性。据式(49)所示的制导律，构造图3所示的制导系统模型，其中，初始方向误差角 ε=5°，落角约束 θf= －45°，Tg=0．5 s，V=300 m/s．

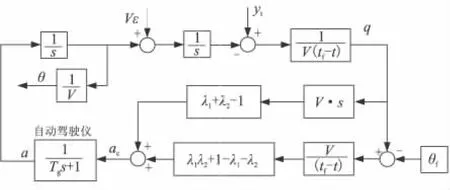
图3 制导系统结构框图Fig．3 Block diagram of guidance system

图4～图6分别为不同特征根作用下的弹道、弹道倾角及加速度曲线。为了使对比更直观，图6中没有考虑驾驶仪动力学对加速度的影响。由图4～图6可看出，特征根的不同取值决定了制导律是否具有约束终端落角的能力;当特征根取值靠近EOGLIAC的特征根时，所对应的制导律对终端落角的约束也越严格，而当特征根取值靠近EPNGL的特征根时，所对应的制导律已经完全失去了对落角的约束能力。

需要强调的是，尽管每一对可能的(λ1，λ2)取值都能找到最优解释，但这并不能保证其都能达到与EPNGL或EOGLIAC类似的制导性能，但特征根取值越靠近EPNGL或EOGLIAC，则所对应的制导律特性与EPNGL或EOGLIAC也越接近。

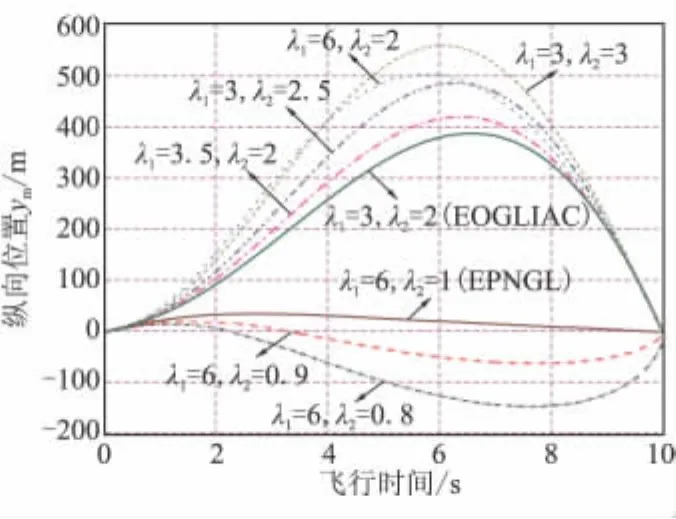
图4 不同特征根下的弹道对比曲线Fig．4 Comparison of the trajectories for different CR

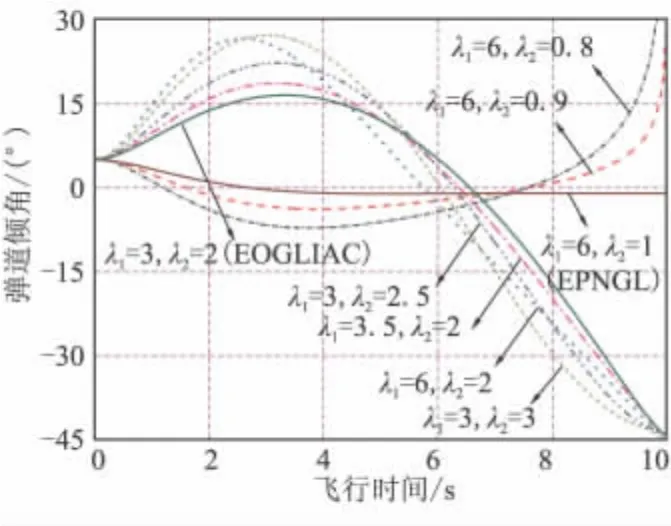
图5 不同特征根下的弹道倾角对比曲线Fig．5 Comparison of the flight path angles for different CR

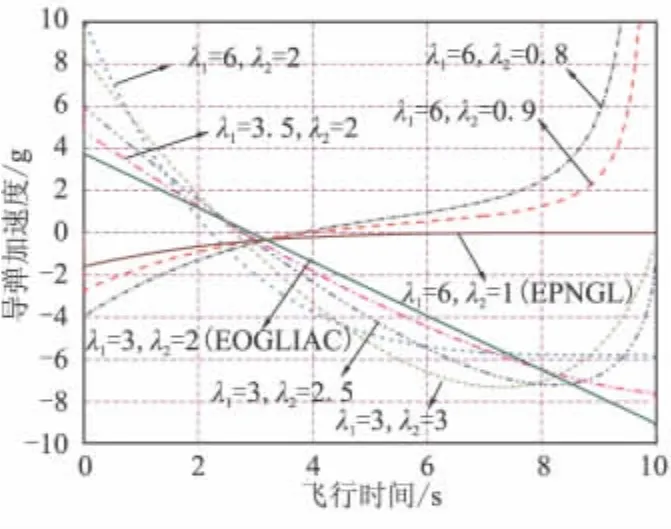
图6 不同特征根下的加速度对比曲线Fig．6 Comparison of the accelerations for different CR

图7、图8所示的不同特征根下的脱靶量和终端落角误差曲线也直接印证了上述结论。

因此，尽管逆最优制导律的提出将制导律的2个特征根(或导航系数)从有限的点/线扩展到几乎所有的正实根，但对任意选择的一对特征根，并不能保证其一定具有与EPNGL、EOGLIAC等类似的制导性能，每一对特征根都需要精细的挑选和严格的考核，而以EPNGL、EOGLIAC等为典型代表的常规最优制导律已经得到广泛的应用，经过了充分的工程检验，在这个意义上，EPNGL、EOGLIAC等还是工程最优的。

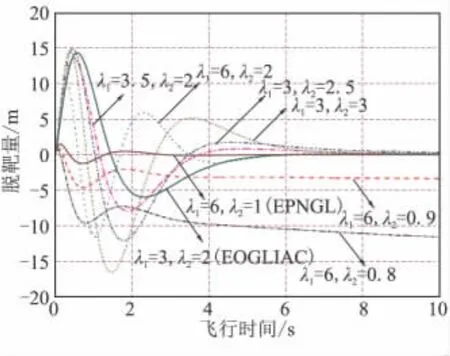
图7 不同特征根下的脱靶量对比曲线Fig．7 Comparison of the miss-distances for different CR

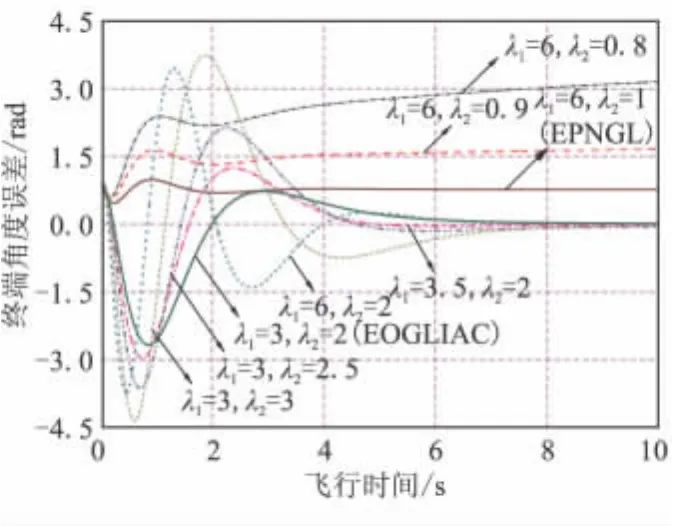
图8 不同特征根下的终端角度误差对比曲线Fig．8 Comparison of the terminal impact angle errors for different CR

5 结论

(1)通过建立相对于终端弹目连线的导弹运动方程，概括了典型的能量最优制导律，分析了其特征根分布范围。将制导律的2个特征根从有限的点/线扩展到几乎所有的正实根，提出了制导律的逆最优问题。详细讨论了逆最优问题中性能指标加权矩阵的构造过程，给出了加权矩阵和Riccati矩阵的计算公式。通过将控制权矩阵选为time-to-go的负n次幂函数的形式，对加权矩阵的求解进行了举例说明。

(2)选取了多组具有代表性的特征根，对不同特征根下制导律的制导特性进行了全面的仿真研究。研究结果表明，尽管每一对可能的特征根取值都能找到最优解释，但这并不能保证其都能达到与EPNL或EOGLIAC类似的制导性能，特征根取值越靠近EPNGL或EOGLIAC，则所对应的制导律特性与EPNGL或EOGLIAC也越接近。但特征根的取值范围要满足哪些限制条件才能达到与EPNGL或EOGLIAC类似的性能，尚有待于后续进一步的研究。尽管如此，文中通过逆最优问题的研究，拓展了最优制导律的内涵。

［1］ Zarchan P．Tactical and strategic missile guidance，5th edition［M］．Virginia:AIAA Inc．，2007:31-50，541-569．

［2］ Garnell P．Guided weapon control systems［M］．Beijing:Beijing Institute of Technology，2003:297-364．

［3］ Ryoo C K，Shin H S，Tahk M J．Energy optimal waypoint guidance synthesis for antiship missiles［J］．IEEE Transactions on Control Systems Technology，2010，46(1):80-95．

［4］ Ohlmeyer E J，Phillips C A．Generalized vector explicit guidance［J］．Journal of Guidance，Control，and Dynamics，2006，29(2):261-268．

［5］ Ryoo C K，Cho H，Tahk M J．Time-to-go weighted optimal guidance with impact angle constraints［J］．IEEE Transactions on Control Systems Technology，2006，14(3):483-492．

［6］ Ryoo C K，Cho H，Tahk M J．Optimal guidance laws with terminal impact angle constraint［J］．Journal of Guidance，Control，and Dynamics，2005，28(4):724-732．

［7］ Ratnoo A，Ghose D．State dependent Riccati equation based guidance law for impact angle constrained trajectories［J］．Journal of Guidance，Control，and Dynamics，2009，32(1):320-325．

［8］ Ratnoo A，Ghose D．Impact angle constrained interception of nonstationary nonmaneuvering targets［J］．Journal of Guidance，Control，and Dynamics，2010，33(1):269-275．

［9］ Ben-Asher J Z，Yaesh I．Advances in missile guidance theory［M］．Virginia:AIAA Inc．，1998:25-88．

［10］ Lee Y I，Kim S H，Tahk M J．Optimality of linear time-varying guidance for impact angle control［J］．IEEE Transactions on Aerospace and Electronic Systems，2012，48(3):2802-2817．

［11］ Kalman R E．When is a linear control system optimal［J］．Journal of Basic Engineering，1964，Series D(86):51-60．