离散相似法在空-空导弹数字仿真中的应用①

王志刚，李 伟，张 宁

(1．西北工业大学 航天学院，西安 710072;2．航天飞行动力学技术重点实验室，西安 710072)

0 引言

在空-空导弹火控系统的设计过程中，需要通过大量的数值仿真得到发射包线。目前，国内普遍采用龙格库塔法对导弹的动力学微分方程进行数字计算，并将计算的大量弹道数据加载到火控计算机中，最后用多项式拟合方法进行插值解算。该种方法求解直观，易于掌握，但适用范围受到很大限制，一旦改变导弹参数，软件修改也非常麻烦。针对此类问题，国内外众多学者提出了快速模拟［1－2］方法，但该方法要求很高的仿真速度。随着计算机技术的迅速发展，当前已能做到仿真时间达到导弹飞行时间的数十分之一甚至数百分之一，即所谓的超实时仿真。为了提高仿真速度，可通过数学模型及计算方法的简化获得。

“离散相似法”是将一个连续系统进行离散化处理，然后求得与它等价的离散化模型［3］。从20世纪80年代开始，国内广大学者就将离散相似法用于控制系统的数字仿真中［4－7］。这些研究大多是基于连续的线性或弱非线性控制系统来进行离散相似法的快速仿真研究，很少有将离散相似法用于非线性的动力学系统数字仿真中。本文在合理的简化模型基础上，提出了将离散相似法用于导弹数字仿真中的方案。

1 导弹运动模型的建立与简化

描述导弹详细运动的方程共有16个［8］。显然，用这样一个高达16阶的系统来描述导弹，对于快速仿真是不合适的。要进行快速仿真，必须建立合理简化的数学模型，它既要能真实地反映导弹的弹道特性，又要大量地简化计算。因此，本文采用以瞬时平衡状态下的升力、阻力和侧向力为基础的三自由度质心运动数学模型，建立简化的数学模型的假设条件:

(1)导弹具有弹体滚动角稳定系统，并且速度倾斜角为零;

(2)俯仰、偏航、滚动通道之间是解耦的、无耦合;

(3)瞬时平衡状态下的气动系数对攻角和侧滑角的偏导数为常数。

基于上述假设条件，导弹质心运动方程组可写为

式中 v、θ、ψV分别为导弹的速度、弹道倾角与弹道偏角;x、y、z分别为导弹质心位置坐标;m为质量;g为重力加速度;P为推力;Xb、Xb、Zb分别为与平衡攻角αb和平衡侧滑角βb对应的平衡阻力、平衡升力、平衡侧向力。

2 导弹运动模型的时域离散化

连续系统等价的离散模型可通过2个途径获得:一是对传递函数作离散化处理的频域离散相似模型;二是基于状态方程离散化的时域离散相似模型。本文采用的是第二种处理方式。

2．1 模型离散化处理

从式(1)可看出，导弹运动方程组是一组非线性方程，在用时域离散法前，需要对方程的形式进行修改，把原方程变为形如式(2)的状态方程。

其中

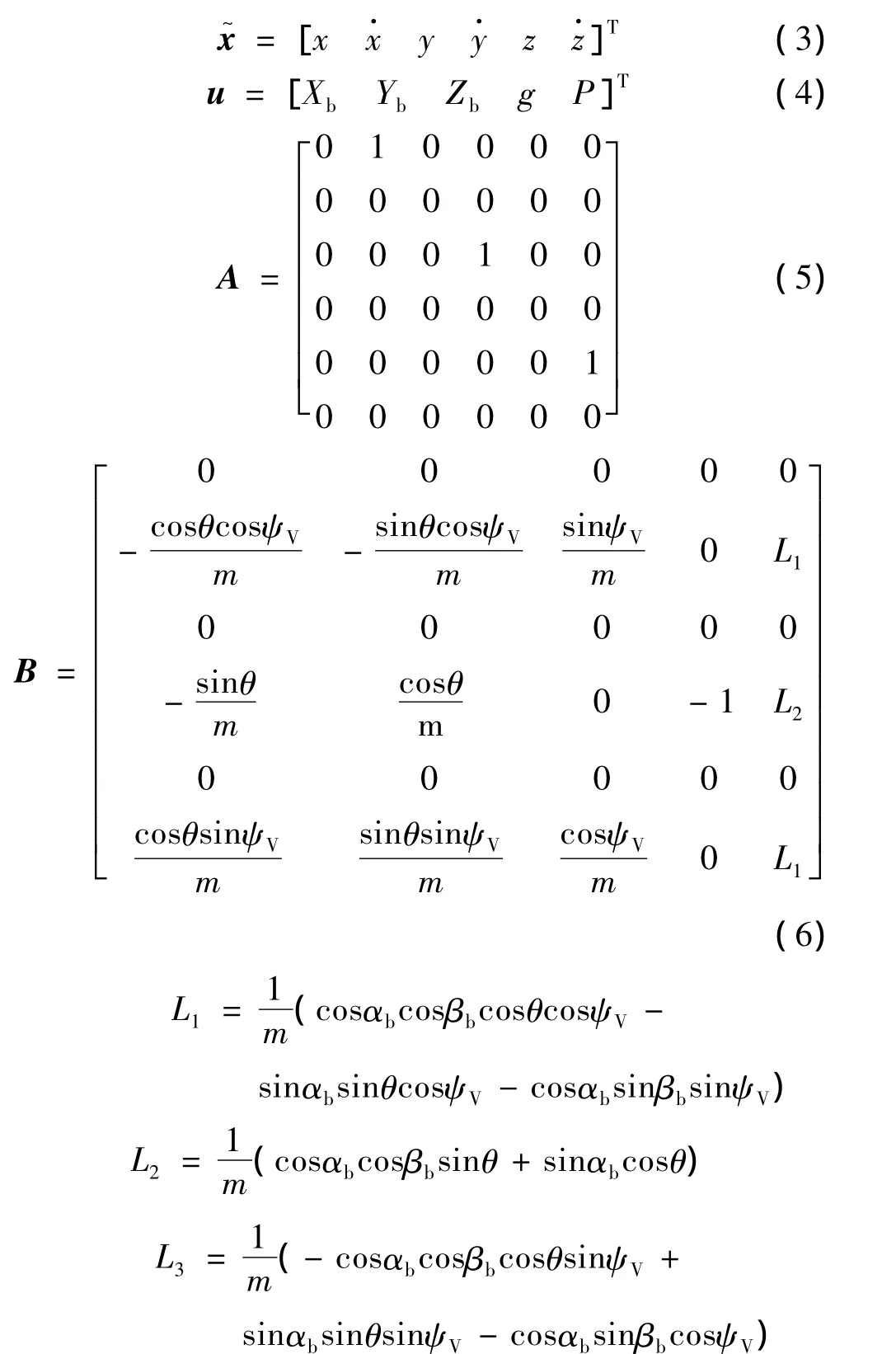
对式(2)所示连续系统进行离散化处理后，可得到系统离散相似模型如式(7)所示:

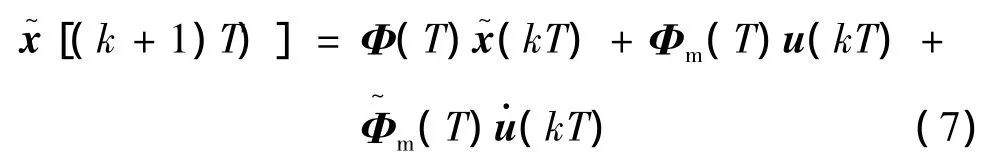
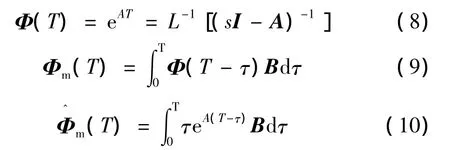
2．2 速度方程

从式(7)可看出，模型输出的速度是在惯性系下的投影。为了研究弹道的相关特性，往往更关心导弹速度的大小以及速度矢量在惯性系中的相对位置关系。因此，根据弹道坐标系和惯性系之间的相对转换关系［8］，可得出如下表达式:

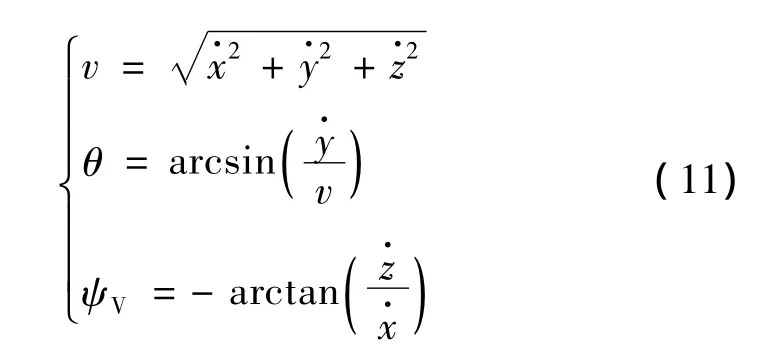
2．3 瞬时平衡关系方程

由于本文采用的是三自由度质心运动模型，气动力的计算只能利用瞬时平衡状态下的攻角αb和侧滑角βb进行解算。αb和βb可通过瞬时平衡关系得到:

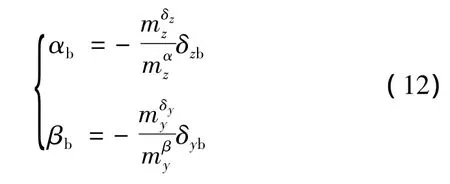
式中 δyb、δzb为平衡舵偏角;为俯仰力矩系数对攻角偏导数为俯仰力矩系数对俯仰舵偏角偏导数;为偏航力矩系数对侧滑角偏导数;为偏航力矩系数对偏航舵偏角偏导数。

2．4 弹目相对运动方程

假设目标运动信息已知，目标相对导弹的位置矢量为 r，它在惯性坐标系上可用(r，qε，qβ)表示

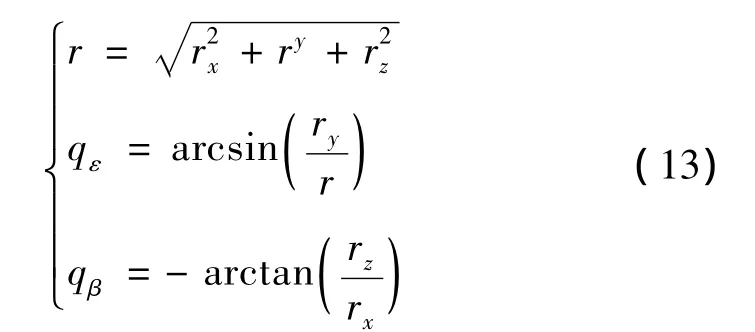
式中 r为弹目相对距离，rx=xt－x，ry=yt－y，rz=zt－z;xt、yt、zt为目标质心位置在惯性系下的投影;qε为视线高低角;qβ为视线方位角。

在导引律算法中，通常还需要弹目相对位置矢量r的速度信息，对式(13)进行求导:

2．5 制导控制方程

快速仿真计算时，采用比例导引律，其形式为

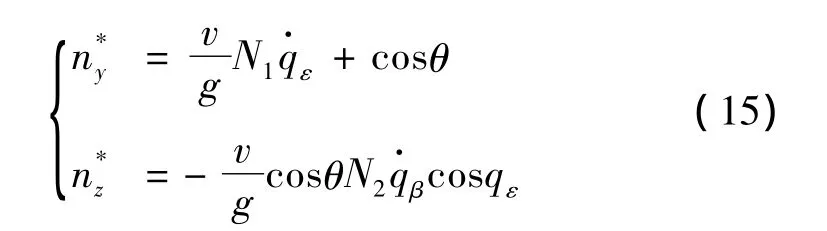
控制方程为

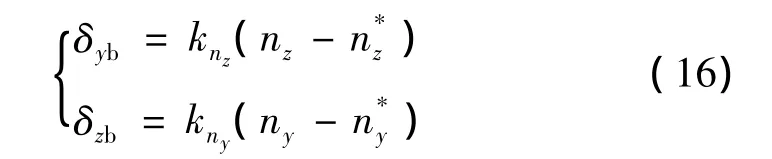
式中 δyb、δzb为平衡状态下的等效偏航舵偏角和俯仰舵偏角;ny、nz为法向过载和横向过载;knz= －0．1、kny=－0．1为控制系数。

3 算例

以AIM-120空-空导弹为对象，针对目标做匀速直线运动和S型机动的2种情况，分别采用本文建立的离散仿真模型与当前常用的快速仿真模型进行对比。

3．1 算例1——变步长积分模型

为提高运算速度，在计算过程中，部分文献［9－10］采用变步长的方法。本节在导弹运动方程组式(1)的基础上，以传统模型［8］(基于龙格库塔法的导弹质心运动仿真模型)的仿真结果为标准数据，将变步长积分模型的仿真结果同其比较。2种模型采用相同的仿真条件，如表1所示。

为了更直观地表现2种模型的差别，现给出2种模型弹道数据做差(变步长积分模型仿真数据减去传统模型的仿真数据)结果，如图1、图2所示。

3．2 算例2——气动系数拟合模型

利用传统的插值算法对气动数据进行计算时，虽能保证一定的精度，但会占用大量的计算机时和存贮单元，不能保证计算的快速性。因此，有些学者［11］从气动系数计算方法上着手来提高仿真速度。基于这种想法，本节利用1stOPT拟合软件，对气动系数进行拟和得到相应的计算解析式，并将其用于弹道仿真中。在使用拟合气动数据前，要将拟合数据同原始数据进行比较，判断拟合误差是否过大，如果过大，需要重新选择拟合方法。限于篇幅，在此仅给出升力系数拟合结果同原始数据的对比。

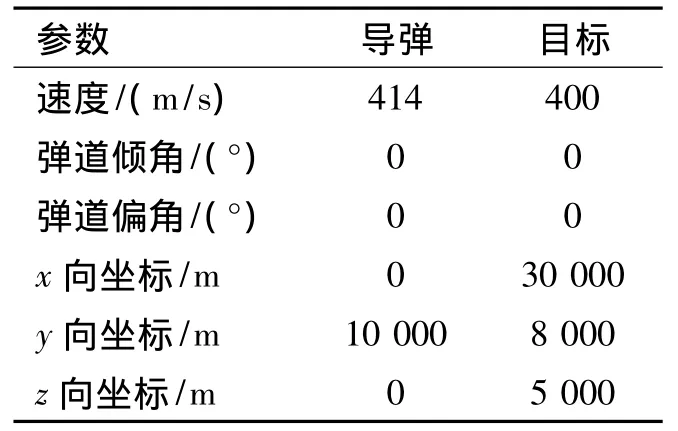
表1 仿真条件Table 1 Simulation conditions

参考AIM-120空-空导弹外形参数，利用DATCOM软件进行气动计算，得到舵不偏转情况下的升力系数，如表2所示。

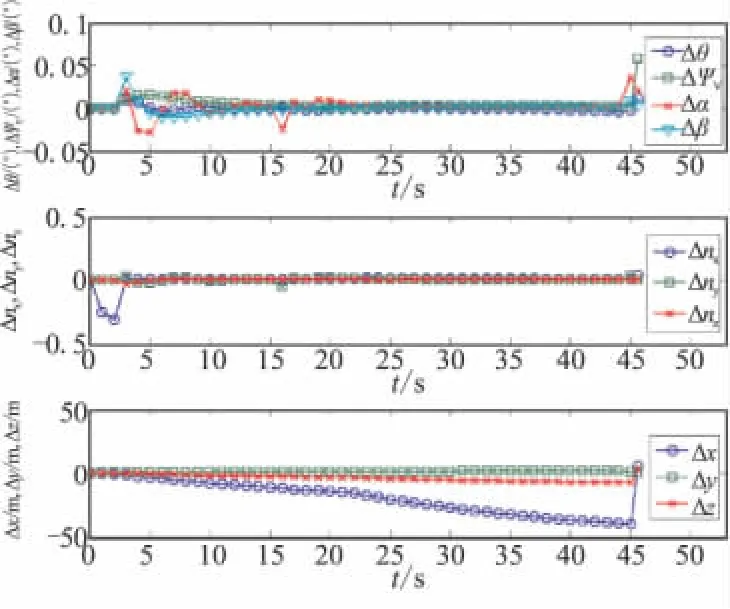
图1 算例1目标匀速运动情况下的对比曲线Fig．1 Comparison curves of target uniform motion of example 1

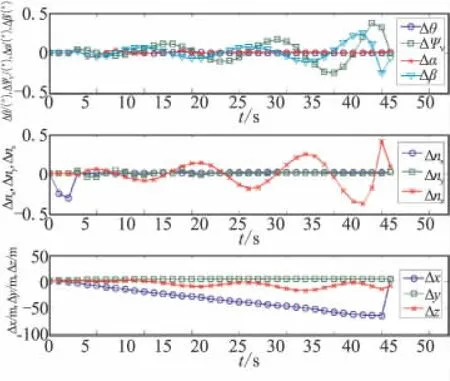
图2 算例1目标S型机动情况下的对比曲线Fig．2 Comparison curves of target S-type motion of example 1

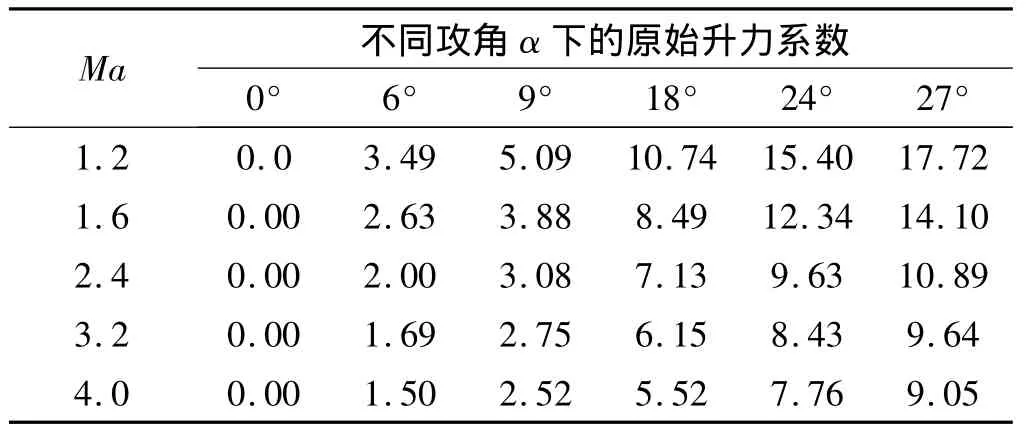
表2 原始升力系数数据Table 2 Original lift coefficient data

在原始升力系数数据基础上，拟和后得到的公式如式(17)所示:

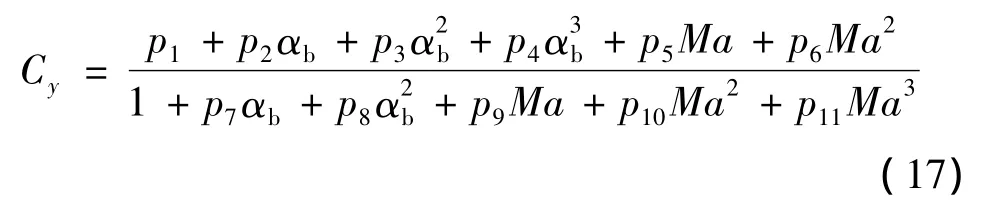
其中，p1～p11为拟合参数:

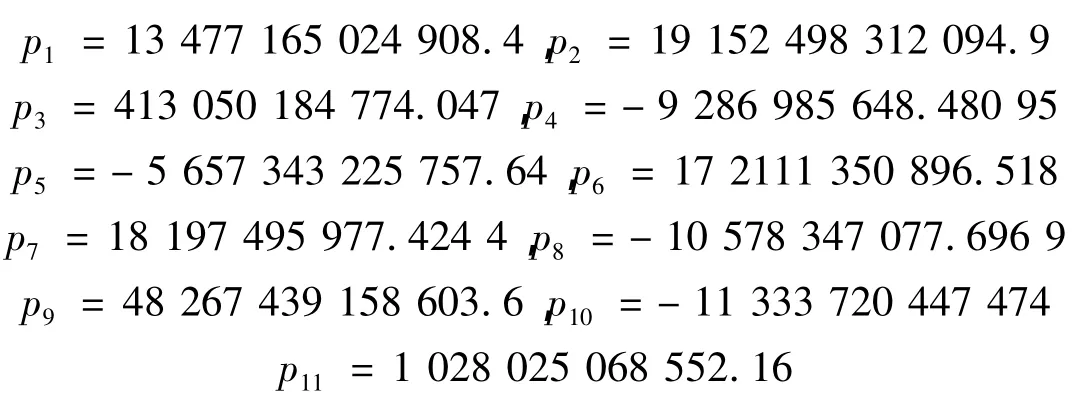
采用升力系数拟合公式(17)，计算出相应的系数值，如表3所示。

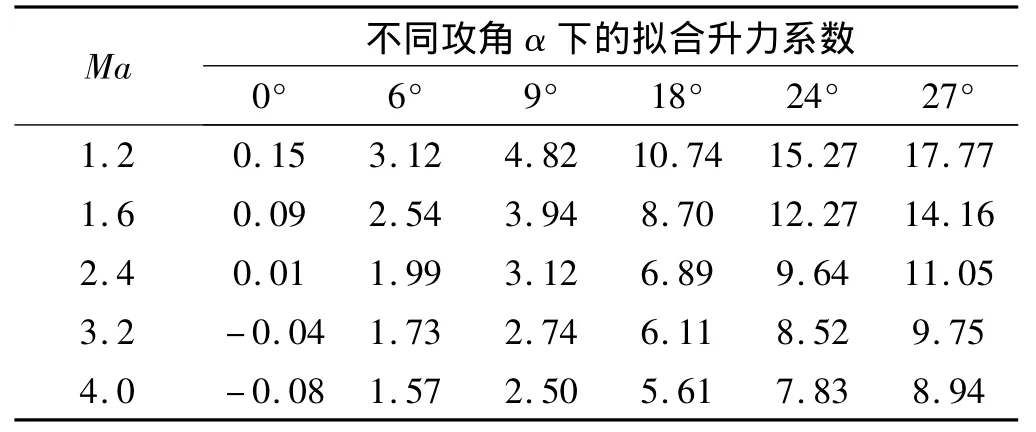
表3 拟合升力系数数据Table 3 Fitting lift coefficient data

由表3可看出，攻角α=0时的拟合结果不满足，升力系数也为0。因此，此处的拟合结果需要强行赋0。下面根据式(18)列出拟合公式解算结果与原始数据的误差百分比，如图3所示。

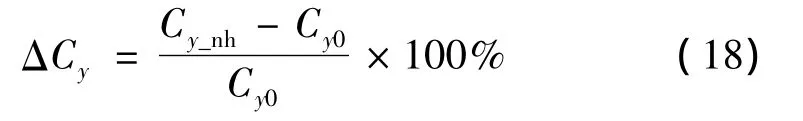
式中 Cy_nh为拟合结果;Cy0为原始数据。

图3 升力系数误差百分比Fig．3 Percentage error lift coefficient

由图3可看出，拟合结果除了在Ma=1．2攻角为6°情况下的误差绝对值超过10%外，其余结果均在±6%以内，拟合结果具有较高精度。由于快速仿真的主要目的是研究导弹的弹道特性或计算攻击区，而不是分析制导精度或导弹飞行稳定性。因此，可将拟合结果应用与弹道仿真。在使用拟合公式(17)时，还需要注意到在负攻角情况下，需要在Cy的基础上加上负号。

参照导弹运动方程组(1)的模型以及表1所示仿真条件，给出气动系数拟合模型同传统模型弹道数据对比结果图，如图4、图5所示。

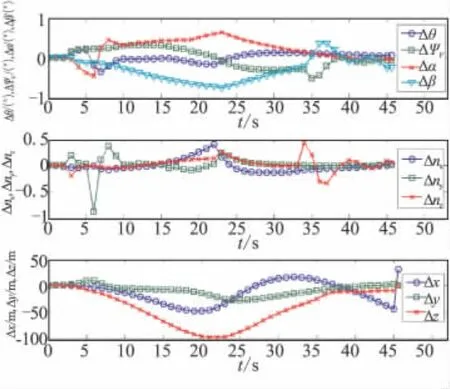
图4 算例2目标匀速运动情况下的对比曲线Fig．4 Comparison curves of target uniform motion of example 2

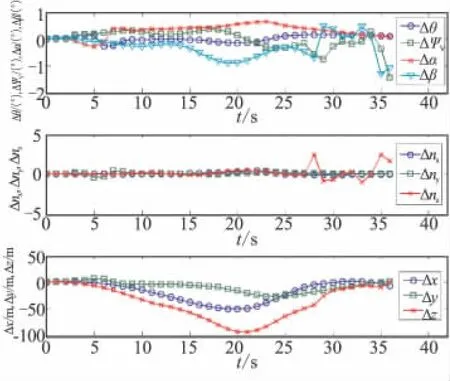
图5 算例2目标S型机动情况下的对比曲线Fig．5 Comparison curves of target S-type motion of example 2

3．3 算例3——离散模型

参照第2节给出的离散仿真模型和表1所示仿真条件，给出离散模型同传统模型的对比结果，如图6、图7所示。

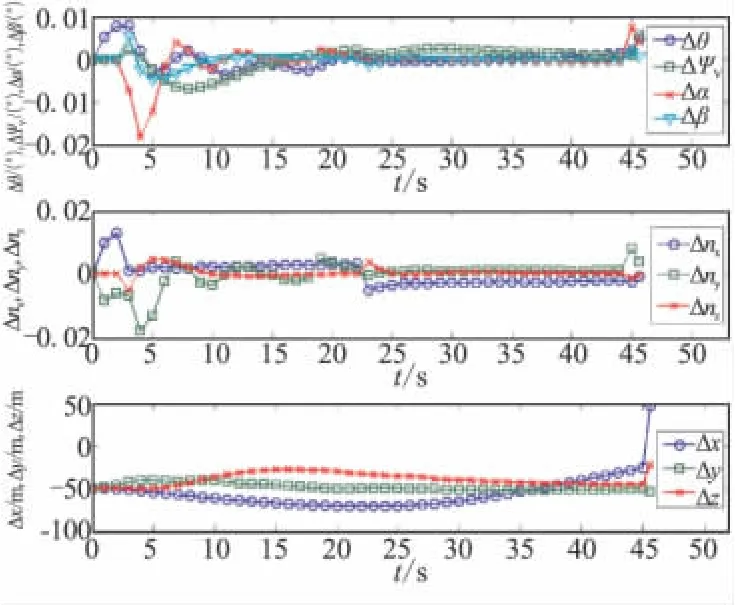
图6 算例3目标匀速运动情况下的对比曲线Fig．6 Comparison curves of target uniform motion of example 3

3．4 结果与分析

上述3个算例是在1台内存为2 GB、CPU主频3．6 GHz的电脑上进行仿真的，各种模型仿真相关数据对比如表4所示。

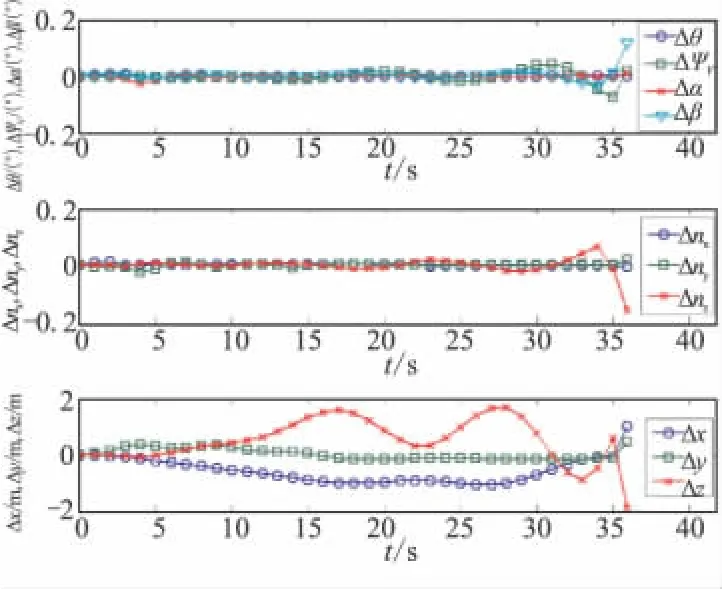
图7 算例3目标S型机动情况下的对比曲线Fig．7 Comparison curves of target S-type motion of example 3

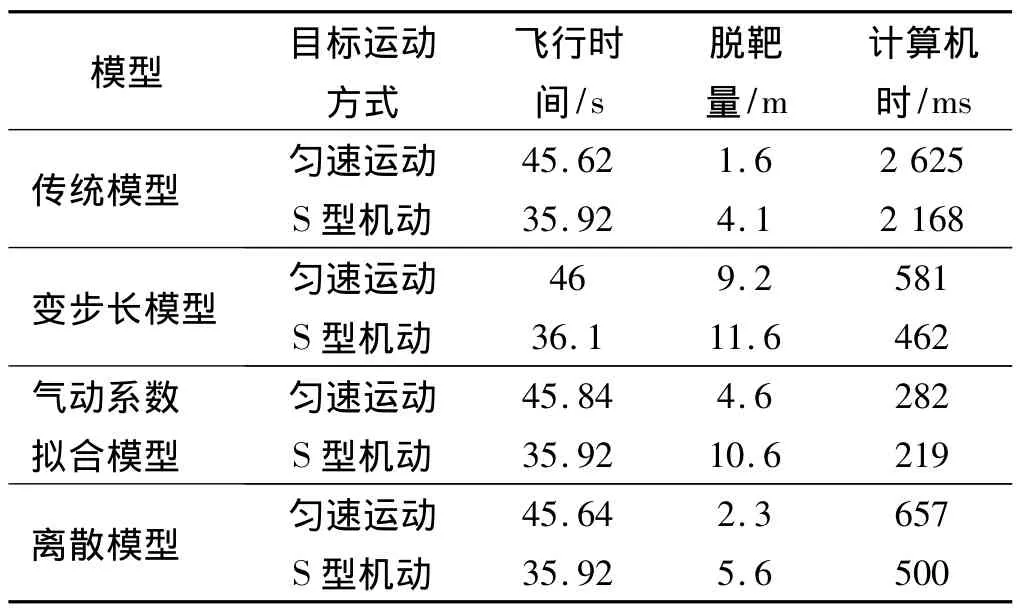
表4 弹道仿真相关数据对比Table 4 Related data comparison of trajectory simulation

从表4结果统计看，相同的仿真条件下，3种快速仿真模型都能满足脱靶量小于12 m的要求，且降低了计算机时。

通过上述仿真结果可看出:

(1)采用变步长积分模型虽能提高计算速度，但对仿真精度带来了一定的影响。从图1可知，目标做匀速直线运动时，变步长积分模型计算的各角度误差在 ±0．1°以内;过载误差在 ±0．5以内;y向和 z向位置误差在－8～5 m之间;x向误差最大达到了－50 m，这是由于攻角的误差引起了阻力和升力的变化，进而改变了导弹的射程。当目标做S型机动运动时，采用变步长积分模型解算的各运动参数，虽然都保持在较小的范围内，但相比目标匀速直线运动情况下的仿真数据误差增大，特别是横向运动参数呈现出发散趋势。

(2)气动系数拟合模型是3种快速仿真模型中减少计算机时最有效的方法，但从计算精度来看，该模型并不能保证很高精度。特别是当目标做S型运动时，气动系数拟合模型计算的运动参数比另外两种快速仿真模型误差要大10～100倍。可见，气动拟合系数带来的误差即便很小，由于误差积累的因素，仿真时间越长，对仿真的精度影响越大。

(3)从图6、图7可知，无论目标做哪种运动，离散模型全程的弹道数据比传统模型只有微小变化，基本可忽略。尽管离散模型相比其他2种快速仿真模型耗时略长，但能以较高精度复现原始弹道，更具可用性。

4 结论

(1)针对空-空导弹弹道仿真模型，本文基于离散相似法建立的离散模型合理可行，可作为空-空导弹快速仿真的一种有效方案。

(2)3种快速仿真方案相比，气动系数拟合模型计算速度最快，约为变步长积分模型和离散模型的2倍，但计算精度是三者中最差的。离散模型与快速积分模型计算速度较接近，但具有很高的计算精度。

(3)针对目标做S型运动的情况，其他2种快速仿真模型运动参数出现较大误差，侧向运动参数甚至呈现出发散趋势。本文所建离散模型对于这种高速机动的目标仍具有较强的适用性，能更好地适应现代战场要求，为载机提供更加有利的发射窗口，更好地完成作战任务。

［1］ 李强，夏群利，崔莹莹，等．空地制导炸弹可攻击区的快速解算方法［J］．兵工学报，2012，33(4):390-394．

［2］ 任宏光，周桢．复合制导空空导弹快速仿真研究与应用［J］．飞行力学，2004，22(1):52-55．

［3］ 肖田元，张燕云，陈加栋．系统仿真导论［M］．北京:清华大学出版社，2000:56-72．

［4］ 肖建．高阶系统的离散相似法仿真［J］．湖南大学学报，1985，12(1):54-66．

［5］ 金炜东．线性定常系统离散相似法仿真的快速算法［J］．控制理论与应用，1993，10(5):599-604．

［6］ 王彦良．自动控制系统计算机数字仿真中状态的非线性约束［D］．长春:吉林大学，2007．

［7］ 周文忠，李果．离散相似法在卫星姿态控制系统设计和数字仿真中的应用［J］．控制工程，1994(2):29-35．

［8］ 李新国，方群．有翼导弹飞行动力学［M］．西安:西北工业大学出版社，2005:37-49．

［9］ 吕铭强，张安．中程空空导弹火控系统评定基准研究［J］．系统工程与电子技术，2003，25(10):1307-1310．

［10］ 杜昌平，周德云，江爱伟．一种空空导弹可攻击区快速算法［J］．西北工业大学学报，2006，24(6):682-685．

［11］ 黄家成，张迎春，等．空空导弹攻击区的快速模拟法求解［J］．弹箭与制导学报，2003，23(4):132-134．