轴对称弹体级间冷分离流场数值模拟与阻力特性①
贾如岩,江振宇,胡 凡,张为华
(国防科技大学航天科学与工程学院,长沙 410073)
0 引言
导弹或火箭通过在飞行中抛弃废重,以获得更高的速度增量,级间分离发生在本级助推器工作完毕与下一级助推器开始工作之间。分离装置工作在下一级助推器点火之前,且分离冲量来源于单独冲量装置的分离形式,称为冷分离。分离装置工作在下一级助推器点火之后,而分离冲量来源于发动机喷流的分离形式,则称为热分离。在常规运载火箭与弹道导弹中,由于气动阻力较大,且作用复杂,一、二级的低空分离较多采用热分离形式,国内外学者对热分离过程流场特性的研究已较为充分[1-5]。低空高速条件下的级间冷分离多见于中小型导弹、需要初始加速的巡航弹以及试验火箭等。针对这类过程中级间流场演变一般规律与分离过程气动力变化机理的研究并不多见。
对于轴对称串联的弹体,低空级间冷分离过程中阻力特性变化直接影响前、后体的轴向加速度,对能否实现分离,避免后体追上前体,甚至发生碰撞起决定性作用。随着轴向相对距离的增加,级间分离前体底部与后体头部之间流场经历低速涡流、斜激波、脱体正激波一系列复杂变化,导致前、后体阻力特性存在明显相互干扰。早期学者依靠风洞实验对特定的前、后体气动力干扰问题进行了定性研究[1]。近年来,CFD技术被广泛应用于运载器[2-4,6-7]、导弹[5,8]、飞行试验[9]等复杂级间流场的预示与气动力的计算。
本文通过对低空超音速条件下等直径轴对称弹体在不同分离距离时的流场进行数值模拟,研究分离过程流场结构变化的一般规律,着重对后体阻力突变前后流场的变化进行仿真分析,以揭示前、后体阻力突变机理。流场的轴对称假设在这一问题中较为理想。但由于实际中级间分离均在零攻角条件下进行,且不对称扰动具有随机性,阐明轴对称假设下级间分离流场一般规律与阻力变化机理实际上是为后续进行真实条件下分离问题研究提供对照分析的基准,对最终形成明确的、可靠的分离机构设计准则具有重要的理论指导意义。
1 物理模型与计算方法
本文研究对象为零攻角飞行的等直径轴对称串联分离弹体,见图1。在理想情况下,弹体外部流场为轴对称状态。此次研究通过数值求解理想气体可压缩N-S方程的方式进行,采用轴对称假设以减少计算量,湍流模型采用经过长期实践检验的标准k-ε方程模型。采用有限体积法离散控制方程,流动方程采用二阶迎风格式离散,通量格式为Roe-FDS,湍流模型方程采用一阶迎风格式离散。前后体物面边界采用无滑移、绝热壁条件。
计算外形前体为锥形头部加圆柱形弹身,后体为圆柱形,且与前体等直径,前体长1.6 m,后体长1 m,直径为300 mm,级间距离ΔL取为直径的倍数。前体头部第一层网格厚度为0.25 mm,距离为4D时,网格总节点数69 980。分别基于总节点数为100 230与180 460的加密网格进行仿真,得到后体阻力系数误差在3%以内,表明网格与计算结果无关。

图1 等直径轴对称弹体级间分离示意图Fig.1 Scheme of stage separation of axisymmetric body
2 方法验证
采用某轴对称弹体在零攻角飞行的阻力系数试验数据,对选择的计算方法进行验证。验证结果表明,计算值与实验值基本一致(图2),最大相对误差为12.3%,利用所选择的数值方法进行流场模拟的结果真实可信。
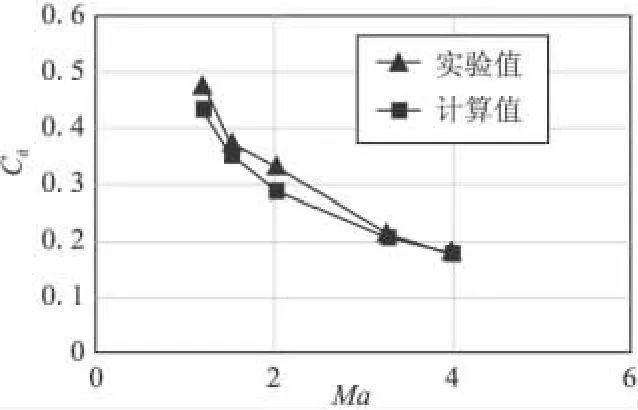
图2 算例验证结果对比Fig.2 Comparison of validation result
3 结果与分析
3.1 2种典型流场结构
通过仿真结果可看出,级间流场结构随距离的变化分为2个阶段,与文献[8]研究结果相似。ΔL<4D范围内,级间区域均由低速涡流填充,形成内部流场,与外部流场之间形成剪切层(以ΔL=2D时流场特征为例,见图3、图4)。此时,涡流由后体头部回流冲击前体底部,致使前体底部压力较高,形成“底部推力”,后体头部完全被前体尾流包围,头部阻力较小。
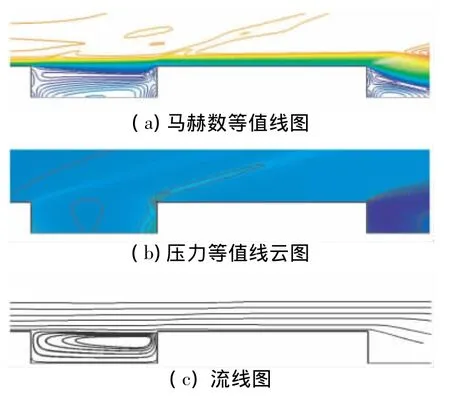
图3 ΔL=2D时的马赫数、压力等值线图及流线图Fig.3 Mach number and pressure contours as well as streamlines for ΔL=2D
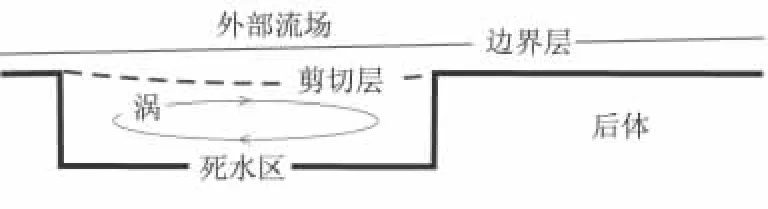
图4 第一阶段流场结构示意图Fig.4 Scheme of flow field structure for the first phase
ΔL=6D时(图5、图6),流场呈现第二阶段典型结构形态,前体底部形成正常超声速尾流场,后体头部出现一定强度的脱体正激波,后体对前体底部流场干扰被隔绝。

图5 ΔL=6D时的马赫数、压力等值线图及流线图Fig.5 Mach number and pressure contours as well as streamlines for ΔL=6D
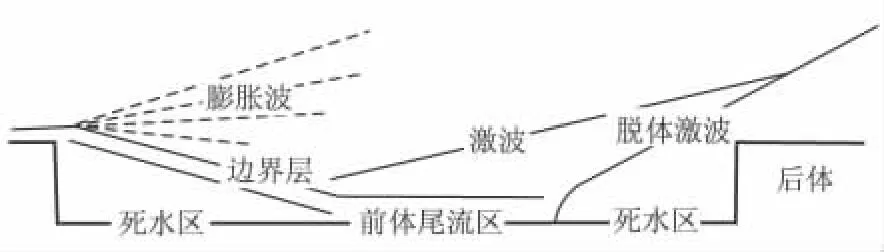
图6 第二阶段流场结构示意图Fig.6 Scheme of flow field structure for the second phase
3.2 过渡阶段流场与阻力特性
本文着重对上述两阶段的过渡阶段进行研究,以此对前后体阻力变化机理进行分析。分别对距离为4.2D、4.4D、4.6D 和4.8D 的级间流场进行模拟,流场结果如图7~图9所示。
级间距离达到4.2D时,剪切层出现颈缩(图7);内部流场在完整的涡流中出现前后2个小涡流区(见图9);后体头部涡流无法完全回流到前体底部,前后涡流区出现压差(图8),此时外部流场变化不大。
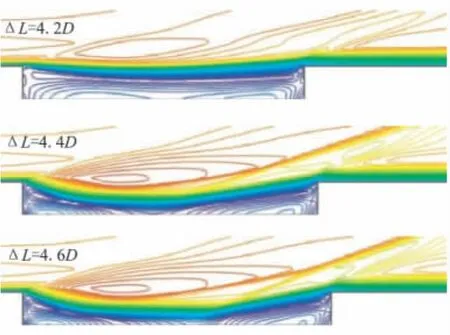
图7 不同级间距离时马赫数等值线图Fig.7 Mach number contours for different stage distances

图8 不同级间距离时压力等值线图Fig.8 Pressure contours for different stage distances
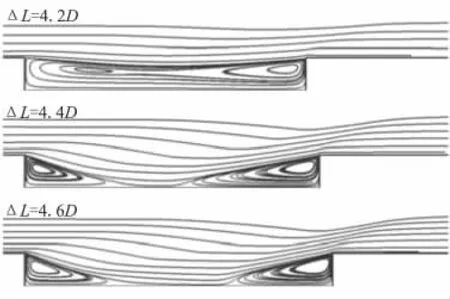
图9 不同级间距离时流线图Fig.9 Streamlines for different stage distances
随着级间距离增加到4.4D,剪切层颈缩加剧,涡流区基本被分割(图9),外部流场在前体尾部发生膨胀。之后,流动被迫转向压缩形成第一道激波,在后体头部之前,流动再次被迫转向压缩形成第二道激波(图7)。此时2道激波距离较近,强度较小,但第二道激波对后体头部区域的增压作用已经较为明显,同时前体底部也出现了明显的压降(图8)。由图10可知,阻力系数已经产生了突增。图11为对称轴附近流动马赫数的分布图。距离达4.4D时,流动马赫数沿轴线分为前体底部反向回流区、前体尾流正向流动区与后体头部反向回流区3个部分,作为后体脱体激波之前的来流最大马赫数只有0.188(x=2.2 m)。因此,后体头部并没有形成脱体正激波。此时,脱体斜激波虽然较弱,但已足以使阻力特性发生突变,突变后,前体基本不受后体干扰,但后体头部流场仍然受到前体尾流干扰,湍流效应使尾流区发生剧烈耗散,流动到达后体头部时,速度明显低于来流,导致后体实际受到的阻力仍偏低,如图10所示。突变后,后体阻力系数仍低于前体阻力系数,并远低于单独飞行时平头圆柱的阻力系数。
距离达到4.6D时,后体头部脱体斜激波变强,激波角增加(图7),对流动的压缩性更强,使后体阻力继续以较快速度增加(图10)。尽管如此,通过图8与图11可看出,脱体正激波仍没有形成(前体尾流正向流动区最大马赫数为0.625,x=2.35 m),后体阻力系数仍小于前体。图10中,下标2为前体,1为后体,b为底部,h为头部。
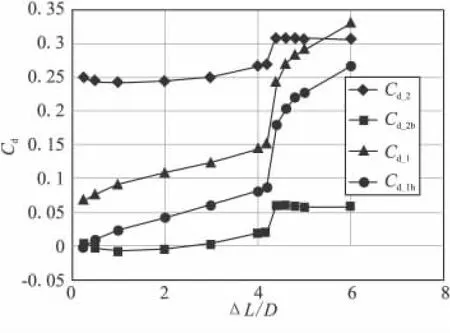
图10 分离过程弹体阻力特性计算结果Fig.10 Calculation results of resistance characteristics during separation

图11 分离区域轴线附近流动马赫数Fig.11 Mach number of flow near the axis of stage separation region
算例结果中,前体底部压力系数(无后体干扰)与试验得到的轴对称弹体底部压力系数以及经验公式得到的底部压力系数较为一致(见图12)[10],这为本次研究提供了进一步的验证。需要说明的是本文算例中的来流雷诺数为 8.782×106(Ma=3)、1.170×107(Ma=4),大于图12所示的雷诺数范围,而文献[10]中已经证明,底部压力系数与来流雷诺数基本无关。因此,仍可用图12中所示数据,对本次计算结果进行验证。
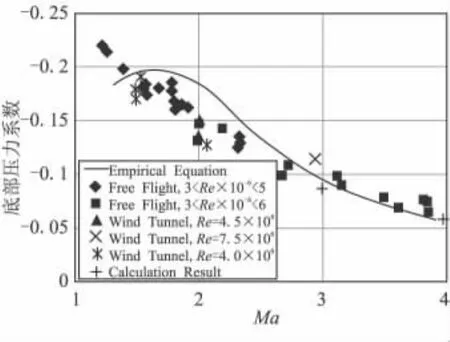
图12 前体底部压力系数验证对比图Fig.12 Comparison validation of base pressure coefficient of forebody
3.3 分离过程阻力估算模型
在分离系统设计初期,准确方便的气动阻力计算模型是分离机构设计的重要工具。将分离过程阻力特性估算模型分为分离初始时与分离过程中两部分,分别进行讨论。
零攻角等直径轴对称弹体的阻力可简单地分为头部与底部的压差阻力、弹身粘性阻力以及其他与弹身连接部件的阻力之和:
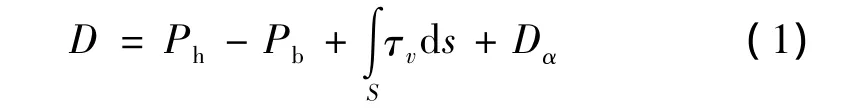
全弹在分离前,阻力可表示为
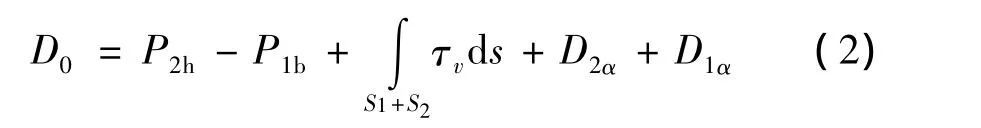
分离开始时前体阻力可表示为
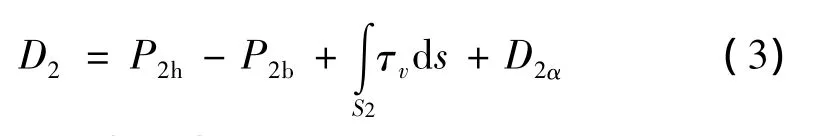
后体阻力可表示为
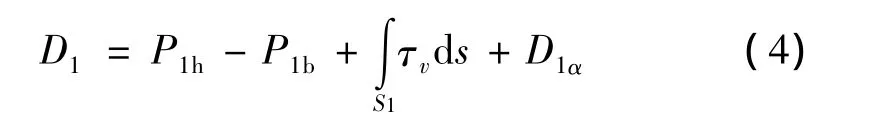
由前文仿真结果可知,分离初期两体距离较近时,前体底部压力与后体头部压力大小相等(见图10),即

因此,由式(1)~式(5)可得:

即分离初始时,后体阻力等于分离前全弹阻力与分离初始时前体阻力之差。式(6)中,D0能够准确得到,而由于“后体效应”的存在,D2难以得到准确结果,根据前文仿真结果,前体阻力随着距离的增大是增加的趋势,受到后体干扰的底部阻力在前体总阻力中所占比重较小。因此,可用前体单独飞行时的阻力系数代替D2,这样既方便计算,也相对保守,利于分离机构的初步设计。
对于分离过程中阻力特性,仿真结果显示,前体底部阻力与后体头部阻力的变化过程更接近于阶跃模型(图10),不同的是前体底部阻力在阶跃后不再受到后体的干扰,达到单独飞行时的流场状态,而后体头部却仍明显受到前体尾流的干扰,阶跃后的后体头部阻力与平头圆柱单独飞行时相比仍存在较大差距。阻力变化估算模型中,阶跃时的分离距离以及阶跃后阻力系数的取值是最重要的参数。真实分离过程流场存在许多不对称因素,如攻角、分离装置干扰、前体尾部流场的湍流效应等,不对称扰动会使后体头部很快偏离前体尾流,部分区域直接暴露在高速来流中,从而加速后体头部正激波的形成,增加前、后体阻力差,加快分离过程。通过研究不对称扰动对分离区域流场的影响,给出近似真实条件下阻力估算模型中特征距离的取值依据,以及阶跃后后体阻力系数的估计值,以指导实际工程设计,这是后续研究中需要解决的问题。
4 结论
(1)级间流场结构随着距离的变化分为2个典型阶段。距离较近时级间区域为涡流主导的流动,前体阻力与自由飞行相比较低。距离较大时,级间区域为激波主导的流场,后体对前体阻力干扰被隔绝。
(2)后体阻力发生突变是头部脱体斜激波的贡献,突变时,后体头部前方并没有形成正激波。阻力突变后,后体对前体的影响已经基本隔绝,但在一段距离内,后体阻力的增加主要来源于头部脱体斜激波的增强,导致后体阻力仍远小于其单独飞行时的阻力,甚至小于前体阻力。
(3)对于等直径轴对称的串联弹体,其分离初始时,后体阻力可利用分离前全弹阻力与分离后前体单独飞行的阻力之差得到,文中证明了这种方法是合理的,且相对保守。
[1] Wasko R A.Experimental investigation of stage separation aerodynamics[R].1961,Lewis Research Center.
[2] 刘君,徐春光,郭正.多级火箭级间分离流动特性的数值模拟[J].推进技术,2002,23(4):265-267.
[3] 黄思源,权晓波,郭凤美,等.火箭级间热分离初始阶段流场的数值模拟[J].推进技术,2007,28(2):113-117.
[4] 高立华,张兵,权晓波,等.火箭级间热分离过程耦合数值模拟[J].清华大学学报(自然科学版),2011,51(4):462-466.
[5] 张文晋,丰镇平.级间分离的流场及热流分析研究[J].推进技术,2003,24(3):240-243.
[6] Pamadi B N,Pei J,Pinier J T.Aerodynamic analyses and database development for ares I vehicle first-stage separation[J].Journal of Spacecraft and Rockets,2012,49(5):864-874.
[7] Mirzaei M,Nia B N,Shadaram A.Numerical simulation of stage separation maneuvers with jet interaction[J].Aircraft Engineering and Aerospace Technology,2006,78(3):217-225.
[8] 周伟江,白鹏,马汉东.弹体级间分离流场特性的数值模拟研究[J].计算物理,2000,17(5):532-535.
[9] Buning P G,Wong T C,Dilley A D,et al.Computational fluid dynamics prediction of hyper-X stage separation aerodynamics[J].Journal of Spacecraft and Rockets,2001,38(6):820-827.
[10] Chapman D R.An analysis of base pressure at supersonic velocities and comparison with experiment[R].Ames Aeronautical Laboratory:Washington,1950.

