λ－Cantor集的对称性研究

曾 莹，胡二琴

（湖北工业大学理学院，湖北 武汉430068）

分形是具有自相似性的一类形状，三分Cantor集是典型的分形几何集合，笔者对此作进一步推广，从度量空间的角度对λ－Cantor集的对称性做进一步分析。

设D是Rn的闭子集，如果对于任意x，y∈D，存在 满 足 0 ＜c ＜ 1，使 得S（x）－S（y）≤cx－y，则称映射S：D→D称为是D 上的压缩（contraction）映射。显然，压缩映射都是连续的。如果等号成立，则称映射S为压缩相似映射（contracting similarity）。

把一个有限的压缩映射族 ｛S1，S2，…，Sm｝，（m≥2），称为一个迭代函数系（Iterated Function System，IFS）；称D的非空紧子集F 为IFS的吸引子（或者称为不变集），若F满足下面的方程

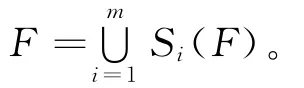
Hutchinson［1981］证明了一个IFS有唯一的一个吸引子，通常吸引子是一个分形［2－4］。

下面介绍Hausdorff度量。用D表示D的全部非空紧子集组成的集类。对于AD而言，所有与A距离不大于δ的D上的点组成的集为A的δ平行体，即

Aδ＝ ｛x∈D，存在a∈A，使得x－a≤δ｝。设A，B是D的两个子集，定义A，B的Hausdorff度量为

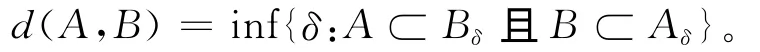
可以验证，d是D上的一个度量，即对任意集合A，B，C∈D，下面三条成立：

（ⅰ）d（A，B）≥0，当且仅当A＝B时等号成立；

（ⅱ）d（A，B）＝d（B，A）；

（ⅲ）d（A，B）≤d（A，C）＋d（C，B）。

引理1 （D，d）是完备度量空间，d是D 上的完备度量，即D中的每个柯西列都收敛到D中的一个元素。

将Cλ称为λ－Cantor集，当λ＝时，Cλ就是我们通常所说的Cantor三分集。

定义两个字母的符号空间Ω＝｛0，1｝!，并引入下 面 度 量： 设 x，y ∈ Ω， 令 dΩ（x，y） ＝2－inf｛n：xn＋1≠yn＋1｝，［4］

引理2 （Ω，dΩ）是完备度量空间。

证明 设 ｛ωn｝是Ω中的Cauchy列，则任意n≥1，存在N（n），当m，m′≥N（n）时，有d（ωm，ω）＜2－n。从而当m≥N（n）时，ωm和ωN（n）的前n项相同。

令a＝ ｛an｝＝ ｛ωN（n）的第n项｝，则dΩ（a，ωm）≤2－n对m≥N（n）成立。从而a为Cauchy列的极限列。证毕。

故

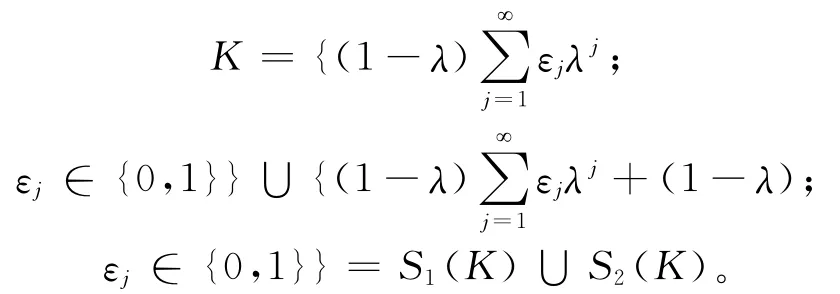
其次，证明K是闭集。令f：Ω→R是由下式定义的映射：

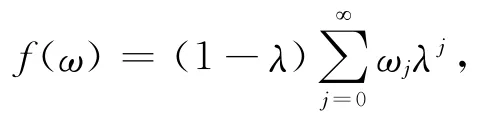
其中ω＝ω1ω2ω3…，而ωj∈ ｛0，1｝。

下一步证明f（ω）是连续的。

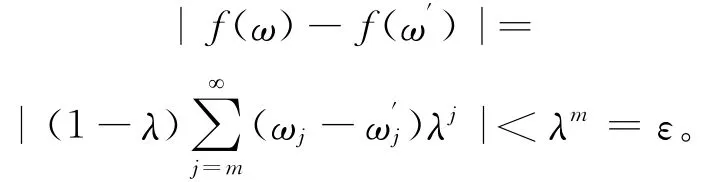
所以f（ω）是紧度量空间的连续映射象，从而K＝f（ω）是个闭集。

由于K满足集方程，而且是非空闭集，故K也是IFS的不变集，由不变集的唯一性，得到Cλ＝K。

最后证明对称性。

［1］ Munkres J R.拓扑学［M］.北京：机械工业出版社2006：204－205.

［2］ Falconer K.分形几何［M］.北京：人民邮电出版社2007：113－118.

［3］ Hutchinson J E.Fractals and self－similarity［J］.Indiana Univ.Math.1981，30：713－747.

［4］ 文志英.分形几何的数学基础［M］.上海：上海科学技术教育出版社1999.