风荷载对超高模板支架稳定性影响的数值分析

王翠英，刘金程

（湖北工业大学土木工程与建筑学院，湖北 武汉430068）

近年来，我国大力发展基础设施建设。随着各种技术的发展与突破，以及各种施工工艺的愈加成熟和工程管理的进一步规范，我国出现了许多高度高跨径大的高大建筑。较大的高度对模板支架体系的安全性能提出更高要求，但由于作为临时支撑结构，并没有建筑本身设计那样严格规范。国内在高大模板支架体系的研究中，对于扣件模型的模拟就可分为铰接模型、半刚性模型和刚接模型三种［1］；对于钢管脚手架与地面的接触分析又分为铰接和刚接两种［2］，规范并未给出合理的模拟模型以及整体承载力计算公式。模板支撑体系作为高大构件，水平荷载特别是风荷载的影响必须予以考虑，而规范只是给出了风荷载计算公式，且只是一个静力学公式，显然对于具有动力性质的风荷载是不够准确的。此外，材料的缺陷、设计的不合理以及管理的不规范都将严重制约模板支撑体系的正常使用及发展。

本文通过大型有限元软件ANSYS建立符合实际工况的模拟模型，设计不同的架体搭设高度，采用动力学模拟风荷载对模板支架体系的影响［3］，从理论上研究风荷载对超高模板支架体系的稳定性影响。

1 力学及有限元模型

1.1 结构分析模型

结构分析是对指定结构在承受预计荷载及发生外部变化（例如，支座移动及温度变化）所进行的预计分析。ANSYS结构分析包括结构静力分析和结构动力分析。结构静力分析是用来计算在固定不变的载荷作用下结构的效应，即由于稳态外荷载引起的系统或部件的位移、应力、应变和力。一般情况下，结构静力分析不考虑惯性和阻尼的影响，适合求解惯性及阻尼的时间相关作用，对结构响应的影响并不显著的问题。结构动力学分析用来求解随时间变化的荷载对结构或部件的影响。与静力学分析不同，动力学分析要考虑随时间变化的力荷载以及对阻尼和惯性的影响。ANSYS可进行的结构动力学分析类型包括：瞬态动力学分析、模态分析、谐波响应分析及随机振动响应分析。结构动力学分析的最终目的就是在确定的动力荷载作用下，结构的内力位移以及反力等量值随时间变化的规律，从而找出其最大值，作为设计、分析或验算的依据。还可以认为，其主要任务是把只适应于静力荷载的结构分析标准方法加以推广，使之也可以在动荷载的分析中加以应用。因此，可以把静荷载视为动荷载的一种特殊形式。

1.2 风荷载动力学模型

高层建筑主要考虑的动荷载是风荷载作用下的动力反应。风荷载可分为对结构作用为静力性的平均风和对结构作用为动力性的脉动风。风对结构的作用不能简化为静力，必须考虑动力的作用。脉动风荷载作用会（包括顺风向、横风向旋涡干扰力）引起高耸结构的振动反应（包括动内力、动位移、振动加速度）。风荷载作用是以外荷载形式沿结构高度方向分布，这种方式的动力源产生结构的动力响应［4］。

1.2.1 脉动风荷载 脉动风下结构风响应的性质是动力的，又是随机的，因而应按随机振动理论进行分析，脉动风作用下，运用随机振动理论，对结构进行动力反应分析，必须知道脉动风速功率谱函数。

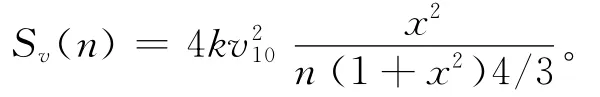
式中，Sv（n）为脉动风速功率谱；k为地面粗糙系数；v10为距地面处的平均风速；n为脉动风频率。

1.2.2 脉动风压功率谱函数 脉动风压荷载可以表示为位置与时间的分离函数，

f（t）规格化的功率谱

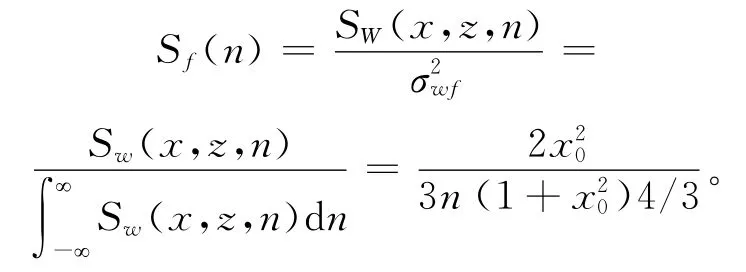
1.2.3 脉动风荷载模拟 设作用在结构上的脉动风荷载向量为｛P｝，根据脉动风压与脉动风荷载的关系，推导得到脉动风荷载的自功率谱密度函数

由于高层结构风荷载在其竖向相关性影响较大，由此可以定义高层结构上作用的脉动风荷载的自功率谱密度函数为

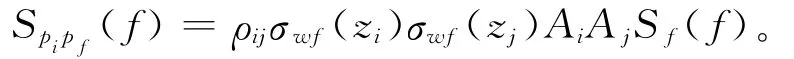
式中，ρij为脉动风荷载的相关系数。

2 数值模拟计算与分析

2.1 数值模型的建立

2.1.1 计算假定与简化

1）模型底部与地面接触为固接约束接触类型。

2）用弹簧单元模拟直角扣件的半刚性特征。

3）风荷载模拟中假定风载是时间的正弦函数。

4）模板支撑体系失稳状态为整体失稳。

2.1.2 模板支架模型参数设置 本文建立的数值模型根据《扣件式钢管脚手架安全技术规范》（JGJ130－2011）［5］对模板支架进行设定，设定步距为1.2m、立杆间距为1.0m×1.0m。模型设定了模板高度H和风荷载两个变量，通过设定不同的模板高度［6］，进行了14组模拟分析，通过是否加载风荷载来模拟风荷载作用对模板支撑体系的影响。模板支架体系参数设置见表1。

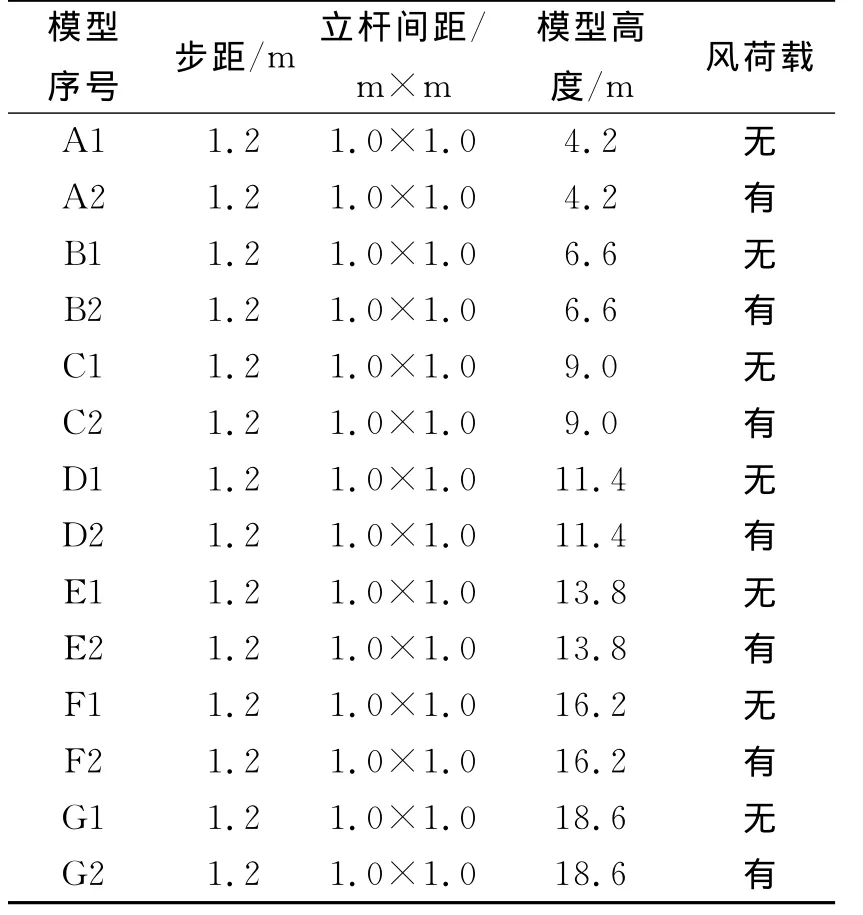
表1 模板支架体系参数

模型立杆组合模式采用横向八根立杆和纵向八根立杆排列，底部截面示意图如图1。

图1 底部截面示意图

2.2 有限元模型的建立

本文模拟根据《建筑施工扣件式钢管脚手架安全技术规范》（JGJ130－2011）［5］设定钢管外径D ＝48.3mm，钢管壁厚T＝3.6mm，钢管弹性模量E＝2.06×1011Pa，泊松比γ＝0.3，钢管密度ρ＝7 850kg／m3。该模型建立采用梁单元Beam188来模拟支撑体系中的钢管。模型底部与地面为固接约束接触类型，构件连接采用半刚性模拟。有限元模型如图2所示。

图2 有限元分析模型

2.3 数值模拟数据分析

2.3.1 风荷载作用下的横向变形 在ansys计算时，该模型假定三维有限元模型风荷载为X风向一个平面上的加载方式，支撑体系模型在风荷载作用下引起结构的非线性的响应，支撑体系模型产生X方向上的横向位移。有限元模型变形见图3。

图3 有限元模型变形图

A2、B2、C2、D2、E2、F2、G2七组数值模型除了支撑高度变化外，采用相同的立杆间距、步距等模型搭设尺寸，同样按照高度变化施加风荷载，通过模拟计算支撑体系模型在风荷载作用下，模型在X风向上的横向变形，并对模型计算结果进行对比处理，采用设定不同模型高度，从数值上分析风荷载随着支撑体系模型高度的变化产生影响的作用效应值。支撑高度与横向变形关系见图4。

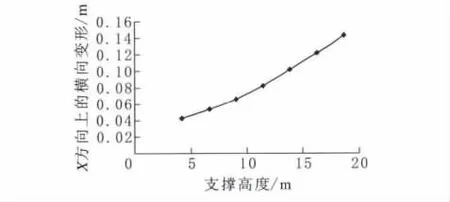
图4 高度变化与横向变形关系图

通过图4分析得出，在风荷载作用下，模板支撑体系在发生模板支架失稳破坏时会产生横向变形，并且随着支撑体系模型高度的上升，模型在X风向上的横向变形逐渐变大。由此可以得出，在进行模板支撑体系的模拟计算中，单纯的将模型体系简化为轴心受压杆件是不够严谨的，应该充分考虑模板支撑体系在支撑过程中，由于风荷载的作用产生的横向变形，特别是高支撑模板体系风荷载作用效应将更为明显。在进行模型计算时，由于横向变形的存在，模型支撑体系不再是轴心受压杆件而是偏心受压体系，以及构件在风荷载等横向荷载的作用下产生的偏心诱发荷载，非线性承载力分析比线性承载力分析更加符合实际工况。

2.3.2 风荷载对支撑体系承载力的影响 风荷载对模板支撑体的影响，最终还是风荷载作用下，模板支撑体系整体承载力的变化。本文进行了A1、A2、B1、B2、C1、C2、D1、D2、E1、E2、F1、F2、G1、G2一共14组模型计算。可分为 A1、B1、C1、D1、E1、F1、G1和A2、B2、C2、D2、E2、F2、G2两组实验组模型，前一组实验组为无风荷载作用下，支撑体系随支撑高度变化承载力变化的计算，后一组实验组为有风荷载作用下，支撑体系随支撑高度变化承载力变化的计算。有限元模型采用几何非线性计算模板支架体系的极限承载力，对两组模拟结果进行对比分析，反映风荷载对支撑体系非线性极限承载力的影响。风荷载作用下支撑高度与非线性承载力的关系曲线见图5。

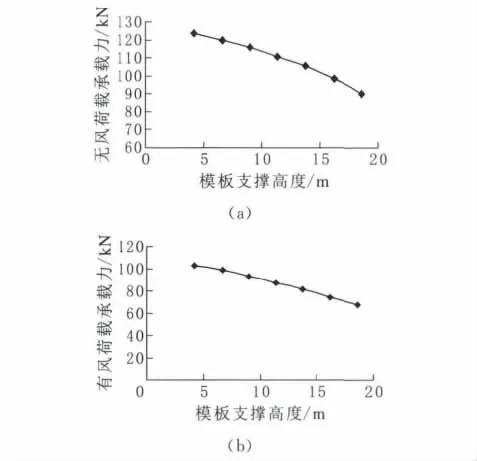
图5 风荷载作用下支撑高度与非线性承载力的关系曲线

图5 表示风荷载作用下支撑高度与非线性承载力的关系。本文将无风荷载作用下模板支架体系承载力和有风荷载作用下的模板支架体系承载力进行对比，并通过降低比例来反映风荷载的影响效应值（表2）。

表2 风荷载影响效应

由图5可以看出，随着模板支撑体系支撑高度的升高，其整体承载力变低。由表2可以看出风荷载作用下，模板支撑体系整体非线性承载力要比不考虑风荷载作用的模板支撑体系承载力要低。并且随着支撑高度的变高，风荷载影响效果更明显。在支撑高度为11.4m时，模板支架体系承载力降低程度已经达到20%以上。随着更多高度、跨径大的高大建筑的产生，模板支架体系的支撑高度将越来越高，因此，风荷载对模板支撑体系的影响必须予以考虑。

2.3.3 数值结果与规范对比 我国现行规范并未对钢管脚手架整体稳承载力给出计算公式。规范假定钢管脚手架支撑体系为轴心受压构件，不考虑偏心受压，从而将整体离散为各个轴心受压立杆来分析，给出了轴心受压立杆的承载力稳定性计算公式。《建筑施工扣件式钢管脚手架安全技术规范》采用“概率极限状态设计法”，根据《建筑施工模板安全技术规范》（JGJ162－2008）［7］，模板支架立杆极限承载力

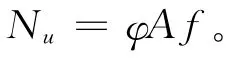
式中φ为轴心受压构件的稳定性系数，根据长细比λ按规范取值，A为立杆截面面积，f为钢材的抗压强度设计值。

按规范计算单根立杆承载力后，再直接叠加所有立杆的承载力而成为整体承载力。将规范计算的承载力与模拟计算得到的结果进行对比（表3）。

表3 模拟计算与规范计算承载力值

由表3可以看出，模拟计算承载力要小于规范计算承载力，前四组计算结果对比可以看出，在支撑高度较低时，按照规范先计算单根立杆承载力，再叠加计算整体承载力的要远远大于模拟计算承载力，规范计算结果已经不能反映实际钢管脚手架支撑体系的整体承载力。后三组实验对比，规范计算承载力比较符合实际钢管脚手架支撑体系的整体承载力，但其值也比模拟计算结果大20%～40%。其结果有此差异的原因主要有：首先，规范将模板支撑体系看成为轴心受压构件，忽略了其偏心荷载的影响；其次，规范将整体结构离散为单根立杆的承载力稳定性计算，却没有给出适合计算整体承载力的计算模型与公式。

3 结束语

通过建立符合实际工况的钢管脚手架数值分析模型，探讨了模板支撑体系模型在风荷载作用下的结构响应，并将模型整体承载力与规范进行对比分析得到如下结论：

1）超高模板支架作为高层构件在风荷载作用下，要考虑其偏心荷载的影响，

2）风荷载作用下模板支架的稳定承载力会降低，特别是超高模板支架体系在设计时应予以考虑。

3）模板支架体系应该作为一个整体，计算其整体承载力，规范应该给出适合整体承载力计算的模型与公式。

［1］ 胡长明，王 静，葛召深，等.扣件式钢管模板支架计算模型研究［A］／／崔京浩.第19届全国结构工程学术会议论文集（第Ⅲ册）［C］.北京：中国力学学会工程力学编辑部，2010：333－339.

［2］ 汪 冬.扣件式钢管模板支架稳定承载力理论分析与试验研究［D］.天津：天津大学图书馆，2009.

［3］ 曾凡奎，刘学兵，胡长明，等.高大模板支架承受的两种特殊荷载分析［J］.青岛农业大学学报（自然科学版），2007，24（04）：308－309.

［4］ 刘立卫，隋杰英，刘 兆.高层结构脉动风荷载模拟［A］／／崔京浩.第16届全国结构工程学术会议论文集（第Ⅲ册）［C］.北京：中国力学学会工程力学编辑部，2007：90－93.

［5］ 中国建筑科学研究院.JGJ130－2011建筑施工扣件式钢管脚手架安全技术规范［S］.北京：中国建筑工业出版社，2012.

［6］ 闫 鑫，胡长明，曾凡奎，等.顶端伸出长度对高大模板支架稳定承载力的影响分析［J］.施工技术，2009，38（04）：73－81.

［7］ 沈阳建筑大学.JGJ162－2008建筑施工模板安全技术规范［S］.北京：中国建筑工业出版社，2008.