最容易跳起的位置在最高点吗

金 逊

(安徽省临泉一中，安徽 临泉 236400)

1 问题的提出

在曲线运动部分，一般的教辅资料都有物体在竖直轨道内做圆周运动的问题.图1所示，是常见的一种物理情景.笔者研究过多种教辅资料，发现它们在讨论轨道对地面压力最小或最容易跳起的条件时，都犯了同样的错误:不加分析，直接以圆周运动的物体到达最高点作为临界条件进行求解.如《3年高考 2年模拟·物理》［1］，《试题调研·高考必备题 1000 例》［2］，《金版新学案》［3］，《精讲精练》［4］等资料均是如此处理.这些资料均认为，物体在最高点时对轨道的作用力处于竖直方向.因此，物体在最高点时，轨道对地面的压力最小.笔者研究后发现，物体在最高点时对轨道竖直方向的作用力不一定最大.相应的，此时轨道对地面压力不一定最小，即轨道最容易跳起的位置不一定在物体圆周运动的最高点.物体做圆周运动的条件与轨道跳起的条件不一定相同.

2 无动力自由圆周运动

2.1 错解实例

下面以《3年高考2年模拟》中的一个试题为例来具体说明(为与后面的表述一致，图的序号及表示物理量的字母有调整).

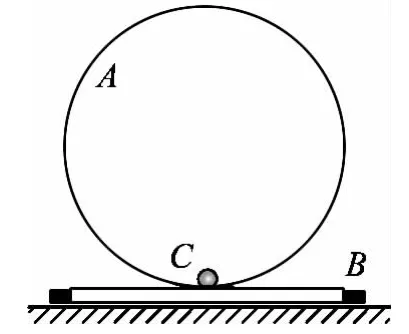
图2

如图2所示，竖直环A半径为r，固定在木板B上，木板B放在水平地面上，B的左右两侧各有一挡板固定在地上，B不能左右运动，在环的最低点静放有一小球C，A、B、C的质量均为m.现给小球一水平向右的瞬时速度v，小球会在环内侧做圆周运动，为保证小球能通过环的最高点，且不会使环在竖直方向上跳起(不计小球与环的摩擦阻力)，判断瞬时速度必须满足的条件.

该书的解答如下:

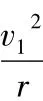
2.2 两者的临界条件一定相同吗

乍一看，以上分析合情合理.处理物体在竖直面内的圆周运动问题时，我们几乎是不假思索地从最高点分析临界条件.从而形成了一种定式思维，碰到竖直轨道内的圆周运动问题，必从最高点分析其临界条件.因此，大部分师生看了上述解法后，表示了对该解法的认可.但是，这种解法是错误的.

尽管物体与轨道之间满足相互作用力等大反向，但物体能否做完整的圆周运动，与轨道能否跳起需要分析的力以及判断的方向并不一致.物体能否做完整的圆周运动，关键要分析沿半径方向的受力情况，判断其与轨道的弹力是否减为0.而轨道能否跳起，则关键要考虑竖直方向受力情况，分析轨道与地面的弹力是否减为0.也就是说，轨道跳起的临界条件与物体做完整的圆周运动的临界条件分析思路不同.因此，临界条件不一定相同.

该错误解法，犯了随意扩大规律使用范围的毛病.物体在竖直轨道内的圆周运动，其临界位置在最高点，从而想当然的认为轨道跳起的临界条件也必须从最高点分析.

2.3 物体在竖直面内做完整圆周运动的临界条件分析

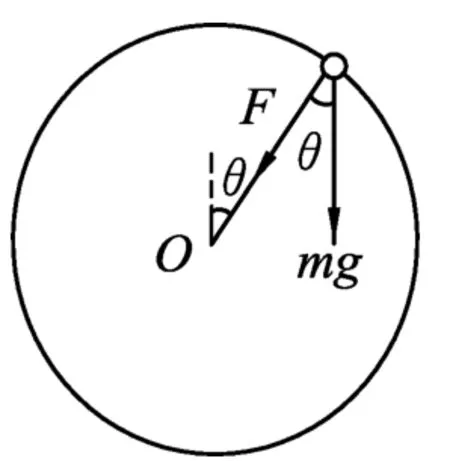
图3

如图3所示，小球在竖直圆轨道内做完整圆周运动.设轨道半径为r，小球在某位置时，半径与竖直方向夹角为θ，轨道对小球的弹力大小为F.小球位于圆心所在水平面下方是不可能脱轨的，以下只讨论小球位于圆心所在水平面上方的情况.根据牛顿第二定律，沿半径方向有

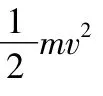
当F=0时，为脱离竖直圆轨道的临界条件.如果此时θ进一步减小，要求F为负即方向相反，沿半径向外.而轨道对小球的弹力是不可能沿半径向外的，这意味着小球已经脱离轨道.

可见，θ越小，小球越容易脱离轨道.所以，小球在竖直圆轨道内做完整的圆周运动，其临界条件是在最高点时轨道弹力为0，重力正好提供向心力.

2.4 特殊值法判断该错误解法不成立

假设小球在轨道最高点时，速度为v1=，满足，此时小球与轨道之间的弹力刚好为0.所以，此位置轨道不可能跳起.

由“2.3”的分析已知，轨道与小球之间的弹力F随θ的减小而减小.如果在最高点小球与轨道之间的弹力刚好为0.则在其他位置时，小球与轨道之间的弹力并不等于0.在圆心所在水平面上方，轨道对小球的弹力斜向下指向圆心，小球对轨道的弹力斜向上背离圆心，如图3和图4所示.小球对轨道弹力存在竖直向上的分力，若轨道重力较小就有可能跳起.

2.5 最容易跳起的临界位置在哪里

既然，最高点不是最容易使轨道跳起的临界位置.那么临界位置到底在哪里?下面分析，在任意位置小球与轨道之间弹力的竖直分力的表达式.进而判断小球在何位置时最容易使轨道跳起?

设小球对轨道的反作用力大小为F'，如图4所示.根据牛顿第三定律，F'与F大小相等，由(1)式得

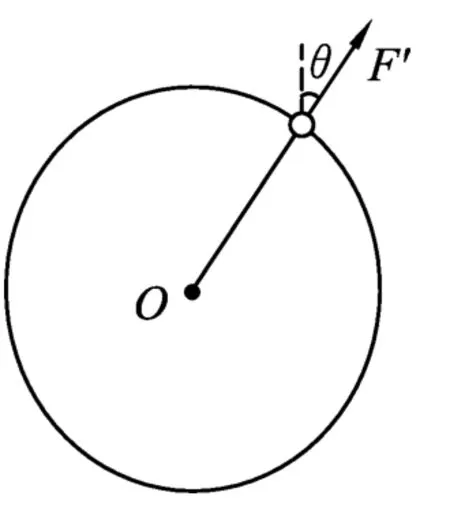
图4

设F'的竖直分量为Fy'，则

越靠近最高点，F'越小，而cosθ在增大，所以不能直接得出Fy'的大小变化情况.由(2)、(3)式得

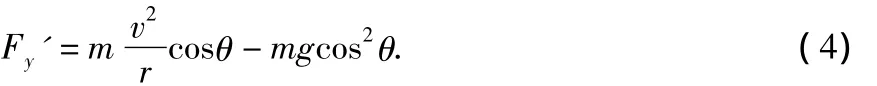
设轨道最低点速度为v0，则从轨道最低点到夹角θ处，根据机械能守恒定律，得

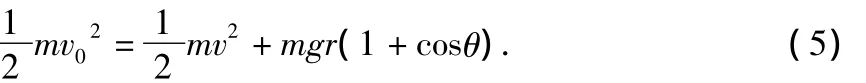
由(4)、(5)式得

上式是关于θ的复合函数，设cosθ=x，则(6)式变为

这是关于x的二次函数.由于小球位于圆心所在水平面上方时，对轨道的弹力才有竖直向上的分量，才可能使轨道跳起.再考虑到对称性，我们只要在0≤θ＜90°范围内分析即可.相应的x的范围为0＜x≤1.

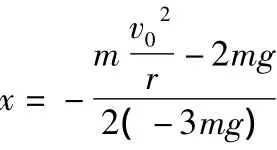
设Fy'极大值为Fym'，则

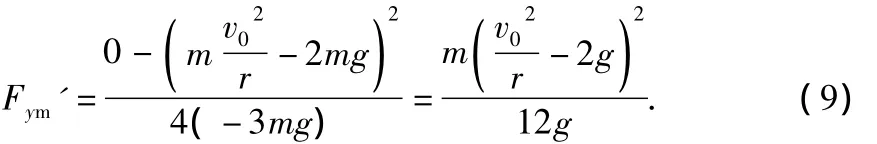
由(8)、(9)式知，v0不同，Fy'取极大值时对应的x不同，相应的θ也不同.即对于不同的初速度v0，Fy'取极大值的位置不同，其极大值Fym'也不同.但是，对于确定的v0，Fy'的极值是确定的，取极值时小球的位置即x、θ均是确定的.

为便于讨论，由(8)、(9)式消去v0，得

设轨道与框架的总质量为M，轨道刚好要跳起时，有

由(10)、(11)式解得，轨道要跳起时

2.6 结论

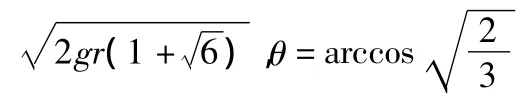
一般教辅资料，不经讨论，不管轨道与重物之间的质量关系，直接在最高点作为临界点求解，其过程和结论一般是错的.只是在质量关系巧合的情况下，其结论才可能是正确的.

3 有动力匀速圆周运动

3.1 实例比较

这里再举一个资料上常见的竖直面内匀速圆周运动的例子.质量为M的电动机，其飞轮上固定着一个小球，小球质量为m，到轴的距离为r，如图5所示.为了使电动机不从地面上跳起，电动机飞轮转动的最大角速度不能超过多少?

该问题与以上讨论的圆周运动比较，不同之处在于这里电动机有动力，小球在做匀速圆周运动，向心力大小不变.故上述因速度变化导致的向心力大小变化无需讨论.共同之处，物体均在竖直平面内做圆周运动.

以上关于重力、弹力、向心力之间关系的表达式是否还成立呢?

考虑到，此例是“飞轮上固定着一个小球”，则飞轮对小球的弹力不一定沿半径方向，所以以上讨论的表达式不再成立，电动机从地面跳起的临界位置需要从新讨论.

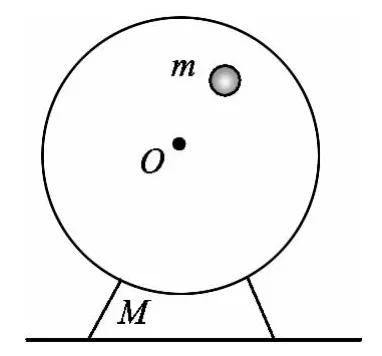
图5

3.2 最容易跳起的临界位置

设小球受到电动机飞轮的弹力为F，由于小球是做匀速圆周运动，其所受合力应指向圆心，如图6所示.这里F的大小方向在不断改变，且变化规律不能简单确定.由于最终是为了寻找电动机(轨道)从地面跳起的临界位置，关键要考虑竖直方向受力情况.这里为了方便讨论问题，我们沿水平、竖直两个方向对力、加速度进行正交分解，分方向应用牛顿定律.

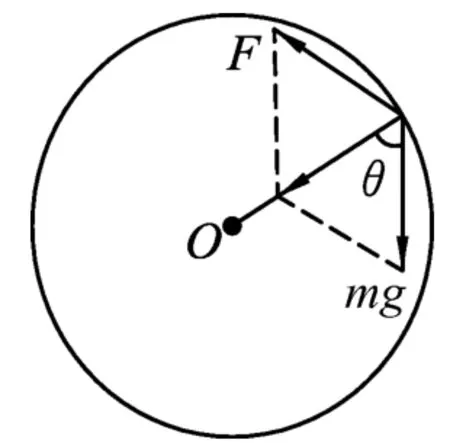
图6

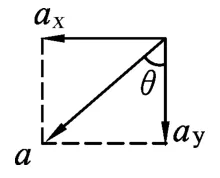
图7

小球在做匀速圆周运动，设角速度为ω，其合加速度即向心加速度，设为a，其竖直分加速度设为ay，如图7所示，则

要使电动机(轨道)跳起，在临界位置小球对飞轮弹力的竖直分力应该向上.根据牛顿第三定律，电动机(轨道)对小球弹力的竖直分力应该向下，设其大小为Fy，由牛顿第二定律得mg+Fy=may.把ay代入，整理得Fy=mω2rcosθ-mg.

设小球对电动机(轨道)的反作用力大小为Fy'，与Fy大小相等，故

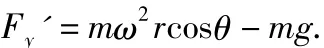
其中，m、ω、r、g均为定值，这是关于θ的三角函数.

由三角函数知识，当 θ=0时，Fy'取极大值，设为Fym'，则

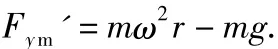
所以，小球在电动机飞轮带动下，做匀速圆周运动，使电动机(轨道)跳起的临界位置，应该在圆周运动的最高点.要跳起的临界状态有Fym'=Mg，代入上式得，要跳起的角速度至少为

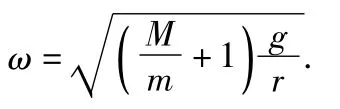
3.3 质疑与释疑

(1)特殊值法分析得出“矛盾”的结论.

有的教师套用无动力圆周运动特殊值法分析，得到在其他位置时，有可能跳起，与以上分析“矛盾”.思路如下.

假设小球在轨道最高点时，满足重力正好作为向心力，此时小球与飞轮之间的弹力刚好为0.自然，此位置轨道不可能跳起.

由于物体做匀速圆周运动，所需向心力大小不变.在其他位置时，小球重力沿半径方向分力作为向心力不够，飞轮对小球应有向里的弹力，补充向心力的不足.自然，小球对飞轮应有向外的弹力，其竖直分力应不为零，若电动机重力较小就有可能跳起.要是这样的话，岂不与以上结论矛盾?问题出在哪里?

(2)释疑解惑.

由前面“2.4”的讨论，知道小球在圆轨道内无动力运动，轨道对小球弹力必沿半径指向圆心.当小球位于圆心所在水平面上方，轨道对小球的弹力斜向下指向圆心，小球对轨道的弹力斜向上背离圆心，导致轨道可能跳起.

而这里讨论的电动机飞轮上的小球做圆周运动，其所受弹力不一定沿半径方向.由于小球是做匀速圆周运动，飞轮对小球的弹力F与重力mg的合力沿半径指向圆心.

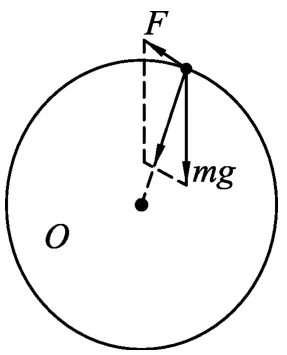
图8

如果在最高点时重力正好作为向心力，由于是匀速圆周运动，其他位置的向心力(合力)大小也正好等于重力.这样，飞轮对小球的弹力总是大致向上的，即便在接近最高点时也是如此，如图8所示.于是小球对飞轮的弹力总是斜向下.自然，是不可能使轨道跳起的.

可见，上述“假设小球在轨道最高点时，重力正好作为向心力”导出“矛盾”的过程有误.以上“矛盾”出现的原因，混淆了两种情况下弹力的方向.

4 总结

4.1 无动力变速圆周运动

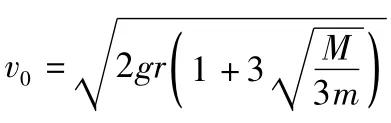
一般教辅资料，直接在最高点作为临界点求解，其过程和结论一般是错的.只是在特殊情况下，其结论才可能是正确的，但过程也是不合适的.

4.2 有动力匀速圆周运动

如果物体在外力作用下做匀速圆周运动，例如小球在电动机飞轮带动下，做匀速圆周运动.使轨道(电动机)跳起的临界位置确实在最高点，但是一般资料对问题的解答缺乏分析论证的环节.

4.3 出错的原因

一般教辅资料出错的原因，在于混淆了物体在竖直平面内做圆周运动的条件与轨道跳起的条件.想当然的认为，它们之间既然存在相互作用力，其临界条件也应该相同.

1 曲一线.3年高考2年模拟·2013年高考物理安徽版.练习册(4版)［M］.北京:首都师范大学出版社，2012(3):19.

2 杜志建.试题调研·高考必备题型1000例 物理(2版)［M］.乌鲁木齐:新疆青少年出版社，2012(6):100.

3 孙明科.金版新学案.新课标.高三物理.课时作业［M］.北京:团结出版社，2012(3):256.

4 王显忠.精讲精练.高考总复习物理(安徽专版)［M］.济南:济南出版社2013(4):62.