非对称直齿圆锥齿轮齿面接触应力分析

张占东，崔永霞，2

（1.山西大同大学 煤炭工程学院，山西 大同 037003；2.太原理工大学 机械工程学院，山西 太原 030024）

0 引言

目前最常见的齿轮是压力角为20°的对称渐开线齿轮，而在工程实践中有大量齿轮副在其整个服役周期中仅依靠单侧齿廓传递单向动力或运动，这不免造成了齿轮副啮合侧齿廓与非啮合侧齿廓的应力状况不同；同时，大量研究表明，适当增大直齿圆柱齿轮啮合侧压力角可以明显降低齿根弯曲应力和齿面接触应力。由此，有学者提出了具有非对称双压力角齿廓的齿轮设计思想［1－3］，即啮合侧和非啮合侧的齿廓渐开线分别由2个半径不同的基圆产生，故而它们的压力角不再相等。

本文针对广泛应用的“8”字啮合型直齿圆锥齿轮，以齿面方程中的啮合侧和非啮合侧齿廓压力角作为基本建模参数，借助ANSYS软件的建模功能和非线性接触分析模块，建立4组在节线处啮合的非对称直齿圆锥齿轮单齿有限元模型，并分析、比较啮合侧压力角对齿面接触应力和齿面疲劳强度的影响规律，为进一步研究非对称双压力角渐开线直齿圆锥齿轮的承载能力奠定基础。

1 “8”字啮合渐开线直齿圆锥齿轮齿面方程

根据直齿圆锥齿轮啮合的基本原理，从直齿圆锥齿轮的切齿方案出发，给出的“8”字啮合型（Octoid）直齿圆锥齿轮齿面参数方程如下：

由于上述齿面几何参数方程是基于展成法加工原理推导得出的，即平面产形刀具与被加工齿轮轮坯作展成运动时，刀具产形面的包络就是被加工齿轮的齿面，故刀具与被加工齿轮的压力角相等，因此可通过改变β来得到不同压力角的直齿圆锥齿轮齿廓方程。

2 齿轮实体模型的创建

本文在ANSYS环境中，采用其自带的参数化设计语言（APDL）和样条曲线（B－Splines）功能，按照自底向上的建模顺序，完成非对称渐开线直齿圆锥齿轮的精确建模，其基本参数见表1。

2.1 啮合侧和非啮合侧齿廓表面的建立

由于非对称渐开线直齿圆锥齿轮啮合侧和非啮合侧齿廓曲线的压力角不同，故本文以β为基本变量，按照下述步骤分别依次建立两侧齿廓表面。

（1）建立大、小端齿廓曲线。在式（1）中，将R 取为大端锥距，β根据该侧齿廓压力角选取。由文献［4］中对坐标系的定义可知，φ＝0对应于球面渐开线上分度圆处的点，φ＜0对应于球面渐开线上分度圆以上部分，φ＞0对应于球面渐开线上分度圆以下部分，故可结合该齿轮的齿顶高系数和顶隙系数分别计算出φ 的正负取值范围。由于该类齿轮齿根过渡曲线的型式与参数方程十分繁复，以至无法直接使用，同时考虑到进行齿面接触应力分析时，该位置处的应力分布对分析结果不会产生显著影响，故本文采用过渡圆角代替。应用ANSYS提供的APDL 语言，并结合有限元计算的精度要求，由齿面参数方程计算得出适当数量的关键点，再利用B－Splines功能即可生成相应的齿廓曲线。小端齿廓的建立与此相似。

表1 齿轮基本参数

（2）建立大端齿顶圆弧和齿根圆弧。每个轮齿对应的圆心角为2π／z，则单侧齿廓对应的圆心角为π／z，故可建立两个夹角为π／z的平面，齿顶圆弧、齿根圆弧分别是球面渐开线上的最高点和最低点到两平面间的圆弧。

（3）借助“蒙皮”命令（ASKIN）依次生成各齿廓面；借助“由线生面”命令（AL）依次生成轮齿的大、小端表面。

2.2 单对轮齿及其有限元模型的建立

为了分析、比较啮合侧压力角对齿面接触应力的影响规律，本文首先建立主动轮的轮齿，其啮合侧压力角分别为15°、20°、25°和30°，而非啮合侧压力角均取为20°；然后利用圆锥齿轮啮合原理建立与之啮合的从动轮轮齿。同时，从计算精度和计算效率考虑，对有限元分析模型进行了适当简化：大端根部周向弧度为3m（m 为模数），主、从动轮径向长度分别为5m、7m，轴向齿宽系数ψR ＝0.3。最终得到的压力角为15°／20°、20°／20°、25°／20°、30°／20°的单对轮齿于节线处啮合的有限元模型如图1～图4所示。

图1 压力角为15°／20°的单对轮齿有限元模型

3 非对称直齿圆锥齿轮齿面接触应力计算结果

由于本文只选取了一对轮齿在节线处啮合这一典型位置开展接触分析，因此在施加边界约束时令从动轮轮齿两侧面及轴孔面上所有节点沿各方向的广义位移均为零，主动轮两侧面和轴孔面上所有节点的径向、轴向位移均为零，但保持其旋转自由度；将作用于齿轮副上的扭矩等效为主动轮轴孔面上各节点上的切向力FY，其计算公式为：

本文中，主动轮所承受的扭矩为1 309N·m。以下将从如下两个角度来分析、比较啮合侧压力角对齿面等效接触应力的影响。

图2 压力角为20°／20°的单对轮齿有限元模型

图3 压力角为25°／20°的单对轮齿有限元模型

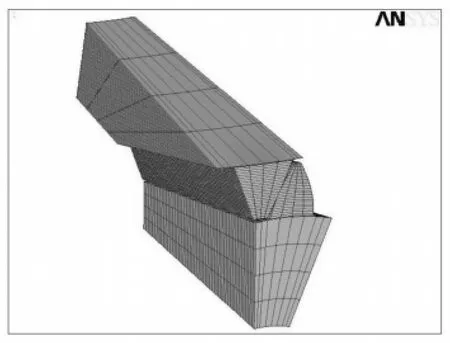
图4 压力角为30°／20°的单对轮齿有限元模型

3.1 大、小端面上等效接触应力的分析

本文利用ANSYS非线性接触分析功能进行了齿面等效接触应力计算，在外加载荷、材料物性参数、齿轮副整体结构参数和非啮合侧几何参数等条件均相同的前提下，得到的大、小端面处的等效接触应力计算结果见表2。

由表2可以看出：齿轮大端的接触应力小于小端接触应力，并且随着啮合侧压力角的增大，两端接触应力都将减小。这说明非对称直齿圆锥齿轮啮合侧压力角对大、小端接触应力均有影响，但由于常规直齿圆锥齿轮压力角多为20°，故在此基础上增大啮合侧压力角，可降低接触应力，但幅值有限。

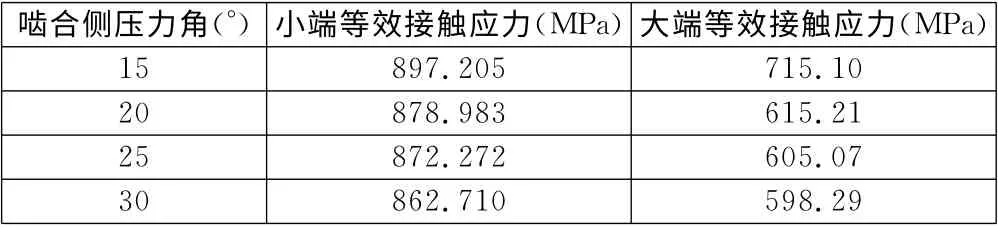
表2 齿轮大、小端面处等效接触应力计算结果

3.2 齿面接触线上应力分布的分析

为了更加全面地分析、研究啮合侧压力角对齿面等效接触应力分布状况的影响规律及程度，图5显示了非对称直齿圆锥齿轮沿齿面接触线的等效接触应力分布情况。

图5 沿齿面接触线的等效应力分布

由图5可以看出，当啮合侧压力角为15°时，接触线上各节点的等效接触应力均要显著大于其他模型中各相应节点上的应力值；而其他3组曲线彼此靠得较近，说明对于这3类非对称圆锥齿轮，齿面接触线上各对应节点间的等效接触应力值保持在同一水平上。

由以上所述可知：适当增大啮合侧压力角可以降低齿面等效接触应力，进而提高齿面抗点蚀能力。但由于目前得到广泛应用的直齿圆锥齿轮压力角为20°，故在此基础上继续增大啮合侧压力角，齿面等效接触应力的降低幅度并不显著。

4 结语

本文将非对称双压力角齿廓齿轮的思想应用于“8”字啮合渐开线直齿圆锥齿轮的设计中，利用ANSYS软件自带的建模工具建立了在节线啮合的非对称直齿圆锥齿轮单齿有限元模型；借助该软件的非线性接触分析模块，研究了啮合侧压力角对接触应力的影响。

［1］ 张玉梅.双压力角非对称齿轮啮合特性及应力分析研究［D］.南京：南京航空航天大学，2005：20－25.

［2］ 徐晓东.非对称渐开线齿轮的啮合特性及应力分析研究［D］.南京：南京航空航天大学，2005：17－28.

［3］ 肖望强，李威，韩建友，等.双压力角非对称齿廓渐开线齿轮的振动分析［J］.中国机械工程，2006，17（6）：645－648.

［4］ 周延泽，吴继泽.直齿圆锥齿轮齿面和齿根过渡曲面方程［J］.北京航空航天大学学报，1993，16（3）：112－120.

［5］ 夏巨谌，陈霞.直齿圆锥齿轮的精确建模及其接触应力的有限元分析［J］.轻工机械，2007，25（1）：69－71.

［6］ 杨生华.齿轮接触有限元分析［J］.计算力学学报，2003，20（2）：189－194.