基于模态叠加法振弦传感器激振力优化分析

申 展，马少杰，张 合

（南京理工大学 机械工程学院，江苏 南京 210094）

0 引言

振弦传感器激振力长期高频率作用于振弦上，该力的合理与否直接影响了振弦式传感器的长期稳定性和寿命，所以激振力大小的设计对于振弦式传感器至关重要。目前国内振弦式表面应变传感器技术日趋完善，但是国内生产的振弦传感器与国外生产的振弦传感器相比，在传感器长期稳定性方面的技术还不够成熟，尤其是激振线圈产生的激振力的设计，基本凭借经验公式和试验，很少利用CAE 分析不同激振力激振后振弦的振动响应。为了提高振弦传感器的长期稳定性和寿命，得到最优激振力，本文利用ANSYS模态叠加法对振弦振动响应进行仿真分析。

1 振弦激振拾振原理

1.1 振弦激振原理

激励振弦振动的目的是测出振弦振动的频率，本文采用单线圈激振法，具体过程如下：由单个线圈进行激振和拾振，将拾到的振动信号传给采集仪，由采集仪对采集信号进行整形、放大等处理，最后输出对应的频率信号。

1.2 振弦拾振原理

振弦激振后振动，由于振弦被置于磁场中，因此它在振动时在电磁线圈中产生感应电动势V，感应电动势V 的频率就是振弦振动的频率，所以其响应信号是一定频率的正弦信号。但是由于振弦传感器的金属外壳不可能完全实现密封，其中的空气阻力以及钢弦两端紧固夹头的作用力将使振弦振动的振幅和能量逐渐减小。因此，振弦的响应信号是按指数函数衰减的阻尼振动信号。其振动表达式为：

其中：β为表征钢弦所受到阻尼大小的阻尼系数；A0为初始振幅；φ0 为初始相位；ω 为角频率。

振弦激励响应信号的波形图如图1 所示。图1中，t0为振动响应初期时间，该时间段内频率信号不稳定；t2为振动响应后期时间，该时间段振动幅值过小，不易采集到信号；故一般取中间段振弦响应时间，即t1时间段。

图1 振弦激励响应信号波形

振弦式传感器测频方法主要有两种：计数法和多周期测量法。计数法是在单位时间内对被测信号脉冲进行计数；多周期测量法是用计数器测量多个周期值。

2 ANSYS模态分析振弦基础频率处振动响应

本文采用某型号手持振弦数据采集仪，该型号采集仪采用扫频激振方式，激励电压为30V 的脉冲电压，要求传感器感应电动势持续时间≥500ms，感应电压≥0.05mV。

2.1 对振弦施加预应力

建立直径Φ0.2 mm、长度L＝90 mm 的振弦模型。当振弦加载上64N 的预压力后，振弦绷紧，同时被拉长了约0.928 9mm，此时绷紧的振弦的固有频率f 可由振弦数学模型计算：

其中：L 为振弦长度；σ为振弦内应力；ρ为振弦密度。

将L＝90mm，σ＝2 229.30 MPa，ρ＝7.85g／cm3代入式（3）可计算出此时振弦的固有频率f ≈2 960.580 1Hz。

2.2 振弦模态分析

在模态分析过程中选择开启预应力影响，将上一步完成的预应力静态分析结果加载到模态分析过程中。

ANSYS模态仿真分析得出的振弦模型的固有频率f＝2 978.1 Hz，与理论计算得到的振弦固有频率f≈2 960.580 1Hz数值基本一致，进一步验证了仿真分析的精确性以及模型建立的合理性。

2.3 振弦模态叠加振动响应分析

完成预应力加载的静态分析和振弦6阶模态分析后，继续对振弦进行模态叠加分析。运用模态叠加分析来确定振弦承受随时间变化的脉冲激励载荷时振弦的动力学响应。

在振弦中间节点22施加一个Y 正方向的脉冲力F＝0.01N，脉冲力持续时间t＝33.5μs（与振弦固有振动周期T 相同）。将该脉冲力F＝0.01 N 以f＝2 978.1Hz的频率加载在振弦上，加载45 个周期脉冲力，振弦达到共振，振动幅值和振动时间的关系如图2所示。

图2 振动幅值与振动时间关系曲线

改变脉冲力的大小，得到不同激振力激振线圈在不同振幅处的振动响应时间，见表1。表1中，A 为该激振力对应的最大振幅幅值。由表1可以看出，激振力的大小变化对振弦振动响应时间的影响较小。对振弦振动幅值的大小影响较大，即影响了振弦内应力的大小，最终影响了振弦式传感器的长期稳定性。当F≥0.06N 时，振幅在0.1×107mm 满足线圈振动响应时间≥500ms的要求。

表1 不同激振力激振线圈在不同振幅处的振动响应时间 ms

3 磁场强度对线圈感应电动势的影响

当振弦振动时，影响了线圈内部的磁场分布，从而使得线圈产生感应电动势，由法拉第电磁定律可得感应电动势E：

其中：N 为线圈匝数；S 为线圈横截面积；Δφ 为磁通变化量；ΔB 为磁感应强度变化量；Δt为时间变化量。

如果加大磁场，即加大了线圈内部的磁感应强度，对于同一振动幅度，磁场越强，线圈感应电动势越明显，值越大，持续时间也越长。建立模型，模型包括一个直径Φ8mm、厚度1 mm 的强磁线圈、铁心、空气、振弦，图3为振弦初始状态磁场分布。图3中，黑色方形线框为铁心，线圈中磁感应强度的变化主要来自于铁心内部磁感应强度的变化。永磁体产生的磁场主要集中在振弦中；图3 中黑线sz 为定义的一条闭合路径，在该路径上对磁感应强度B 进行积分，即得到线圈内部磁通量大小；图3中振弦内部磁感应强度最大值Bmax＝9.207×103T。

图4 为定义路径上的磁感应强度曲线。经过ANSYS后处理POST1中的闭合路径积分命令，将电磁感应强度在闭合路径sz上积分，最终得到线圈内部电磁感应强度Bmax＝3.497 7×103T。

图3 振弦初始状态磁场分布

以上分析为振弦处在静止状态时的磁场分布情况。同理可得当振弦的振动幅值（mm）为0.1×10－1、0.1×10－2、0.1×10－3、0.1×10－4、0.1×10－5、0.1×10－6、0.1×10－7位置处线圈内部电磁感应强度B 的数值，根据公式（4）可以计算出线圈的感应电动势，具体见表2。

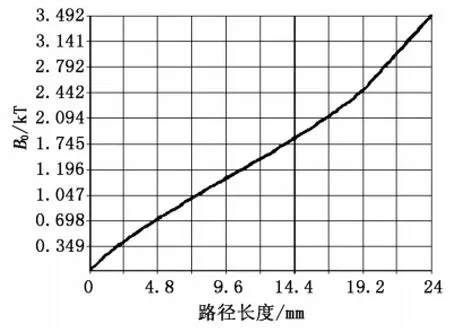
图4 定义路径上的磁感应强度曲线

表2 不同振动幅度对应线圈电磁感应强度和感应电动势

由表2可以看出：振弦振幅越小，线圈感应电动势越小；在振弦振动响应幅值≥0.1×10－7mm 处，线圈感应电动势均能满足E≥0.05mV。

4 结论

（1）激振力的大小变化对振弦振动响应时间的影响较小，对振弦振动幅值的大小影响较大，即影响了振弦内应力的大小，最终影响了振弦式传感器的长期稳定性。

（2）影响线圈振动响应持续时间最主要的因素为线圈所处电磁场的强度。

［1］ 邓铁六.高准确度振弦式传感器研究［J］.山东科技大学学报，2010（1）：52－57.

［2］ 徐承军.振弦式传感器动态测试机理研究［J］.仪表技术与传感器，2011（12）：98－102.

［3］ 张心斌.振弦式应变传感器特性研究［J］.传感器世界，2003（8）：19－21.

［4］ 崔军辉.提高振弦式传感器测量精度的方法的研究［J］.传感技术学报，2009（9）：1276－1279.

［5］ 江修.振弦式传感器的频率敏感机理与应用［J］.传感器技术，2003（12）：22－24.

［6］ Petrovsky，Myron.Instrumentation monitoring of small hydroelectric dams［G］／／Proceedings of the American Power Conference.［s.l.］：［s.n.］，1989：1015－1020.

［7］ Feng Yu，Naren Gupta.An efficient model for improving performance of vibrating－wire instrument［J］.Measurement，2005，37：278－283.

［8］ 王化祥.传感器原理及应用［M］.天津：天津大学出版社，1997.

［9］ Sreeshylam P.Condition monitoring of Prestressed concrete structures using vibrating［J］.International Journal of COMADEM，2008（3）：46－54.