带平衡约束的连续网络设计的模型与算法

谌永荣

(中南民族大学 数学与统计学学院，武汉 430074)

网络平衡设计问题[1]可分为两类:一是对已有路段改造以增加其通行能力,另一则是添加新路段.前者被称作“连续网络设计问题”(CNDP)[2,3],这里的“连续”是指路段通行能力的增加量是连续的; 而后者被称作“离散网络设计问题” (DNDP)[4-6].

对于连续网络设计问题,由于问题中的目标函数是连续的(甚至还可以进一步要求它是可微的、凸的),便于数学处理，所以一直以来受到大家的关注，并且已经有了一些很好的求解算法[7].但在前面的这些文献中，都是假定网络中各路段的行驶费用只与本路段的流量有关，这在很多情况下是合理的，此时问题可建成一个二层规划模型，然后对二层规划模型提出算法.但实际网络中，很多时候各路段的行驶费用不仅与自身的流量有关，还与其他路段上的流量有关，而且路段费用向量关于路段流量变量的雅克比矩阵是非对称的，这时网络设计问题中下层的用户平衡就不能写成一个数学规划模型，本文中将此时的下层用户平衡条件采用变分不等式来描述，并针对该模型设计了求解方法,模型求解中,上层问题采用遗传算法，而下层问题采用对角化方法求解.

1 连续网络平衡设计模型

若以路网的运行费用与投资费用为目标，则有如下模型.

上层问题：

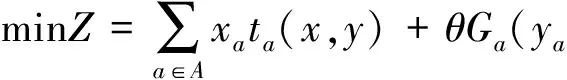
s.t.ya≥0,∀a∈A.

下层问题：

求x*使得∀x∈F′，均有(x-x*)Tt(x*,y)≥0，

其中F′={x|x=Δf,x≤c,Λf=q,f≥0}.

因模型中既有路段变量x又有路径变量f，因此利用关系式x=Δf可将模型中路段变量x去掉，记T(f,y)=ΔTt(Δf,y)，

则下层模型可写为：

求f*使得∀f∈F，均有(f-f*)TT(f*,y)≥0，

其中F={f|Δf≤c,Λf=q，f≥0}.

2 求解算法

2.1 求解上层问题的遗传算法

由于上层问题没有明确的解析表达式，它里面的变量x是由求解下层问题来给出的，所以求解这类问题一般采用启发式算法.遗传算法[8]，它最早由美国密执安大学的Holland教授提出，起源于20世纪60年代对自然和人工自适应系统的研究.该算法通过对生物遗传和进化过程中选择、交叉、变异机理的模仿，来完成对问题最优解的自适应搜索过程.

(1)适应度函数.遗传算法对个体的评价是通过个体的适应度的大小来实现的，所以算法中适应度函数的选取非常重要.这里的适应度函数我们可以直接取为模型中上层规划中的目标函数，即：

(2)编码.由于实数编码不需要编码和解码过程，且精度高，故本问题的求解采用实数编码.

(3)选择算子.本文中采用基本的3种遗传操作算子，即选择、交叉和变异.选择算子采用比例选择算子，也叫赌盘选择，即每个个体被选中并遗传到下一代的概率与该个体的适应度大小成正比.

(5)变异算子采用均匀变异.

2.2 求解下层问题的算法

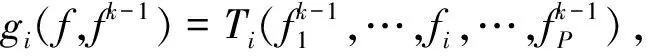
算法步骤如下.

步骤1：初始化.从初始可行点f0∈F开始，令k=1，给定迭代精度ε>0.

步骤2：对角化.求凸规划子问题：

得到解fk.

步骤3：收敛性检验.若‖fk-fk-1‖≤ε，算法停止.否则令k=k+1转步骤2.

算法步骤2中是一个凸规划问题，可以用任何适合的方法求解.

2.3 整体算法的迭代步骤

算法实现步骤如下.

步骤1：初始化.设置最大进化代数T，群体规模M，交叉概率pc，变异概率pm，置t:=0，随机产生M个个体作为初始群体P(0).

步骤2：对每个个体求解下层规划问题的最优解.

步骤3：将上层规划的目标函数作为适应度函数评价所有个体.

步骤4：根据群体中每个个体的适应度值，对P(t)做选择运算、交叉运算和变异运算，P(t)经过3种运算后得到下一代群体P(t+1).

步骤5：终止条件判断.若t≤T，则t:=t+1，转步骤2；否则停止计算，输出最优解.

3 数值试验

本文中的网络如图1所示，两个OD对(1,3)，(5,3),需求量均为55.

图1 道路网络

其中t(x)=Ax+b,Ga(ya)=1.5da(ya)2，

c=(40+y1,45+y2,40+y3,35+y4,40+y5,35+y6,40+y7),

A=

b=(2,2,1,1,3,1,2),d1=d2=2,d3=d4=1,d5=3,d6=d7=2.

计算可得，路段y1,y2,y3,y4,y5,y6,y7能力增加量分别为1.1085，7.3900，3.7126，1.4956，5.8592，2.6921，8.4106，目标函数值Z=1490.0001.

4 结束语

本文针对非对称平衡网络设计问题，采用遗传算法求解，从数值试验结果可知该算法是可行的，而且遗传算法求解速度快，对模型没有特别的要求.在求解下层问题时，采用收敛性快的凸规划的最优求解算法，可大大提高算法的运算效率.

[1]Yang H,Bell M G H.Models and algorithm for road network design: a review and some new developments[J].Transportation Review,1998,18:257-278.

[2]Gao Z Y,Sun H J,Zhang H Z.A globally convergent algorithm for transportation continuous network design problem[J].Optimization and Engineering,2007,8:241-257.

[3]高自友，张好智，孙会君.城市交通网络设计问题中的双层规划模型与算法研究[J].交通运输系统工程与信息,2004,4(1):35-44.

[4]Gao Z Y,Wu J J,Sun H J.Solution algorithm for the bi-level discrete network design problem[J].Transportation Research B,2005,39:479-495.

[5]刘灿齐.交通网络设计问题的模型与算法研究[J].公路交通科技,2003,20:57-62.

[6]桂 岚.交通网络设计的优化模型及算法[J].系统工程,2006,24(12):25-32.

[7]高自友，宋一凡，四兵锋.城市交通连续平衡网络设计:理论与方法[M].北京：中国铁道出版社,2000.

[8]周 明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社,2005.

[9]高自友，任华玲.城市动态交通流分配模型与算法[M].北京：人民交通出版社,2005.