一类带双稀疏过程的双险种风险模型
李学锋,杨薇娜
(中南民族大学 数学与统计学学院,武汉 430074)
破产理论是风险理论的主要研究内容,而风险模型则是风险理论的主要研究对象,其中破产概率是度量风险的重要指标,因此,对破产概率的研究是保险风险模型的重要研究课题.最早的经典风险模型是由Cramer于1930年提出来的.后来,许多学者通过在经典模型中引入一些对模型有影响的因素,比如在文献[1,2]中考虑了利率因素,对经典风险模型进行推广.而且,在很多早期的推广模型中,大多假设保单到达过程与索赔到达过程相互独立,但由于保险业的不断发展,保险公司的规模逐渐增大,保险业务不断增加,而且社会经济环境、生活环境的变化,竞争、利率、通货膨胀率的变化及各种可能发生的灾害等诸多不确定因素的影响,国内外相关研究工作者们也不断对风险模型逐步进行改进.在文献[3] 中,Dufresne和Gerber研究了带干扰的复合Poisson过程的风险模型;文献[4]研究了索赔相关过程的风险模型;文献[5,6]研究了索赔过程是稀疏过程的风险模型并得到了相关结论;文献[7]将单一险种推广到双险种或多险种的风险模型,等等.为了保险公司的长期稳定经营并与时俱进,我们应不断将风险模型合理化,使其更符合保险公司的实际所承担的风险情况.因此,本文就是在上述工作的基础上,将风险模型推广为更一般的情形,即考虑了保险公司的投资利率和通货膨胀率下带干扰项且索赔过程是保单到达过程的稀疏过程的双险种风险模型,并利用鞅分析得到了该模型的破产概率满足的Lundberg不等式及最终破产概率的精确表达式.
1 模型的定义
定义1 设(Ω,F,P)是完备的概率空间(本文所有的随机变量都定义在此空间),则对u≥0,t≥0,保险公司在t时刻的盈余为:
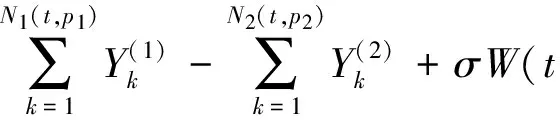
(1)

对上述模型做如下假设:
(1) {M1(t),t≥0}与{M2(t),t≥0}分别是参数为λ1,λ2的Poisson过程;
(2) {N1(t,p1),t≥0}是{M1(t),t≥0}的一个p1-稀疏过程,0 {N2(t,p2),t≥0} 是{M2(t),t≥0}的一个p2-稀疏过程,0 σE[W(t)]=λ1α1+λ2α2-λ1p1β1-λ2p2β2>0, 定义2 保险公司的破产时刻T=inf{t∶t≥0,U(t)<0},最终破产概率为: φ(u)=P{T<∞|U(0)=u}. (2) (3) 假设Li(r)<∞,且显然当r→∞时,有Mi(r)→∞,i=1,2. 引理1 对于盈余过程{S(t),t≥0},存在函数g(r),使得: E[e-rS(t)]=etg(r). (4) 证明 引理2 方程g(r)=0存在唯一正解R,称之为调节系数. 市售金银花在带有温度控制的鼓风干燥箱中干燥成绝干物质作吸湿试验用, 分析纯浓硫酸(重庆川东化工有限公司化学试剂厂)。 证明由引理1知g(0)=0,又: 故: g′(0+)=-(λ1α1+λ2α2-λ1p1β1-λ2p2β2)<0, 所以当r>0时g(r)是凸函数,又g(0)=0,且显然有当r→+∞时,g(r)→+∞,因此,g(r)=0存在唯一正解,记为R.此时称g(r)=0为调节方程,称R为调节系数.证毕. 定义4 对于盈利过程{S(t),t≥0},定义事件流: 引理3 令Mu(t)= (5) 引理4[9]破产时刻T是FS停时. 定理1 风险模型(1)的最终破产概率φ(u)满足Lundberg不等式: φ(u)≤e-r0u(1+i-j), 证明由引理4知T是FS停时,取t0<∞,则易知T∧t0是FS停时,利用有界停时定理知, e-ru(1+i-j)=Mu(0)=E[Mu(T∧t0)]= E[Mu(T∧t0)|T≤t0]P(T≤t0)+ E[Mu(T∧t0)|T>t0]P(T>t0)≥ E[Mu(T∧t0)|T≤t0]P(T≤t0)= E[Mu(T)|T≤t0]P(T≤t0). (6) 又当T<∞时,有u(1+i-j)+S(T)≤0,所以e-r[u(1+i-j)+S(T)]≥1,故 φ(u)≤e-r0u(1+i-j). 定理2 风险模型(1)的最终破产概率为: (7) 其中R为调节系数. 证明根据式(6),取r=R,得: e-Ru(1+i-j)=E[e-RU(T)|T≤t0]P(T≤t0)+E[e-RU(t0)|T>t0]P(T>t0). (8) 以I(A)表示集合A的示性函数,则: 0≤E[e-RU(t0)|T>t0]P(T>t0)=E[e-RU(t0)I{T>t0}]≤E[e-RU(t0)I{U(t0)≥0}], 由于0≤e-RU(t0)I{U(t0)≥0}]≤1,且根据强大数定律可知,当t0→∞时,U(t0)→∞,a.s. 由控制收敛定理可知 在式(8)两端令t0→∞即得证. 本文研究了一类带双稀疏过程的双险种风险模型,所得到的结果对保险公司的经营具有一定的理论指导意义.从最终破产概率可以看出,为确保保险公司的稳定经营,一方面,保险公司必须具备足够的初始准备金;另一方面,公司也不能一味为了获得足够多的保单而盲目降低保费或高额承保.因此,保险公司为降低索赔比例,减小风险,必须在获得尽可能多的保单的同时,还要做好对客户的调查研究,以便厘定合理的保费与索赔额.同时,保险公司也不能忽视投资利率、通货膨胀率及一些随机扰动对公司稳定经营的影响,往往这些因素也直接关系到保险公司的生死存亡.当然,保险公司的实际经营运作情况可能更加复杂,本文所建模型乃至现有的所有风险模型都还有待进一步改进,因此,破产模型仍然是广大相关研究者感兴趣的研究对象. [1] Cai J.Discrete time risk models under rates of interest[J].Probability in the Engineering and Information Sciences,2002,16:309-324. [2] Cai J,Dickson D.Ruin probabilities with a Markov chain interest model[J]. Insurance:Mathematics and Economics,2004,35:513-525. [3] Dufresne F,Gerber H U. Risk theory for the compound Poisson process that is perturbed by diffusion[J].Insurance:Mathematics and Economics,1991,10:51-59. [4] Partrat C.Compound model for two dependent kinds of claim[J]. Insurance:Mathematics and Economics,1994,15:219-231. [5] Luo J H ,Fang S Z.The risk model about that claims are thinning process[J].(In Chinese)Guangxi Science,2004,11(4):306-308. [6] 李学锋.带干扰且索赔为稀疏过程的双复合Poisson风险模型[J].中南民族大学学报:自然科学版,2012,31(2):120-122. [7] Zhang Zhimin,Yang Hu.The compound Poisson risk model with dependence under a multi-layer dividend strategy[J].Appl Math J Chinese Univ,2011,26(1):1-13. [8] 何声武.随机过程引论[M].北京:高等教育出版社,1996. [9] Grandell J.Aspects of risk theory[M].New York:Springer-Verlag,1991.







2 相关引理



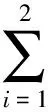

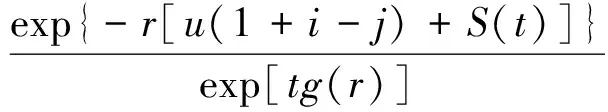

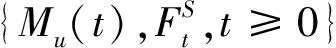
3 主要结果

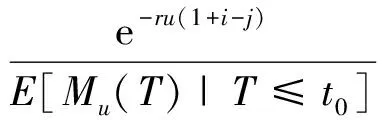

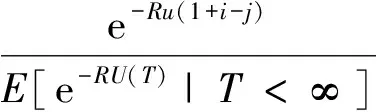

4 结语

