稀疏重构算法

王汗三，陈 杰

(西安电子科技大学理学院，陕西西安 710071)

图像恢复是通过计算机处理，对质量下降的图像加以重建或恢复的处理过程。因摄像机与物体相对运动、系统误差、畸变、噪声等因素的影响，使图像往往不是真实景物的完善映像［1－3］。在遥感图像处理中，为消除遥感图像的失真、畸变，恢复目标的反射波谱特性和正确的几何位置，通常需要对图像进行恢复处理，包括辐射校正、大气校正、条带噪声消除、几何校正等内容。在图像恢复中，对于一个目标函数求极小值，其中要求解的目标函数就是如下的一个不受约束的最优化问题［4－7］

其中，f为Rn→R光滑函数，c为Rn→R 正则函数其中定义域x∈Rn。

对于式(1)具体到l2－l1中，有

其中，y∈Rn，A∈Rk×n，k ＜n，τ∈R+标准欧几里得范数代表lp范数，其中p≥1。式(2)可以用于求出欠定线性方程y=Ax的稀疏近似解［8－9］。

之前涉及上述快速算法包括文献［2］中的方法。在信号处理中关于l1惩罚项的记载参见文献［10］。对于上述最优化问题比较流行的新的应用，就是压缩感知(CS)［9］。最新结果显示，一个稀疏信号相对较少的数据投影，可以包含绝大多数信息。当设置了没有噪声的情况下，通过发现一个可以匹配原始信号的稀疏信号从而精确逼近。

1 方法概述

求解式(1)，可以通过生成一些列的{xt，t=0，1，…}进行迭代求解，首先通过泰勒公式进行展开，并运用MM算法进行简化

其中，αt∈R+。将式(3)进行化简得到

其中，ut∈xt－▽f(xt)。将式(3)中前两项，即(zxt)T▽f(xt)+z－x可以看作一个二次可分离的逼近f(x)，如果对于正则项c(z)是可分离的情况，则式(3)是可分离的形式。对于正则项c(z)是可分离的情况，可写为如下形式

式(2)中的l1正则项显然如式(5)所示，即ci(z)=，当正则项是lpp范数时，也满足式(5)，即正则项是可分离的。

对于正则项是块可分离的情况，如式(6)所示

其中，x［1］，x［2］，…，x［m］是 x 中 m 个不相交的子集。

综上所述，可以得到式(3)每一次迭代的解。当正则项c(x)是可分离的或者块分离的，可以得到有限的极小值。随后可以证明极小值的解收敛。

2 算法

2.1 算法框架

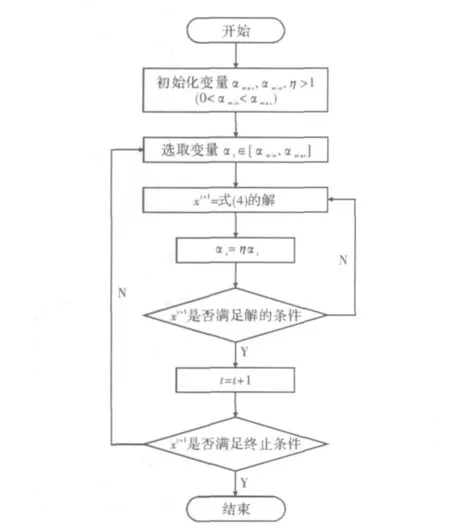
图1 算法流程图

通过选取不同的正则项c(x)，不同的方法选择αt，序号8中xt+1满足的条件不同，可以得到不同的实例化。

2.2 正则项c(x)是可分离的，对于子问题的求解

2.3 对于αt的选取

可以用αtI来代替 Hessian矩阵▽2f(x)，令，st=xt－xt－1，Rt= ▽f(xt)－ ▽f(xt－1)，要求 αtst≈Rt从而得到αt

2.4 解的条件

对于每一次迭代，xt+1满足如下

其中，σ∈(0，1)是一个常量，通常取一个接近于零的数。

2.5 终止条件

终止条件用于迭代程序的最后终止的条件。

2.6 对于的自适应选取

就像GPRS和IST算法，好的初始值对于问题的解是有益处的。关于自适应的选择就是首先给定一个初始的τ0，用于初始化算法，当第二次运行算法程序时，可以自适应地选择一个τ，这样可以减少算法的迭代次数。如果用一个稍大的τ来解决式(1)，然后逐渐缩小到期望值，比直接给定一个较小的τ，通常会更有效。

3 实验结果

前提条件选取A是［20×40］的随机矩阵，分别选取x为不同的稀疏度，ζ=1.1。

图2 参数选取流程

表1 改进后算法与SpaRSA算法的比较

图3 改进后算法与SpaRSA算法的比较

4 结束语

介绍了用于解决大欠定最优化问题的稀疏重构算法SpaRSA，并改进了SpaRSA的解法以及对τ的选取，仿真结果表明，该算法能够更快的求出近似解，在正则项是凸的情况下，可以证明目标函数的极小解是收敛的。

［1］STEPHEN J W，ROBERT D.Sparse reconstruction by separable approximation［J］.IEEE Trance on Math，2009(1):981－986.

［2］CLAERBOUT J，MUIR F.Robust modelling of erratic data［J］.Geophysics，1973(8):826 －844.

［3］AXELSSON O.Iterative solution methods［M］.Newyork:Cambridge University Press，1996.

［4］BARZILAI J，BORWEIN J.Two point step size gradient methods［J］.IMA Journal of Numerical Analysis，1988(8):141－148.

［5］OLSHAUSEN B A，FIELD D J.Emergence of simple － cell receptive field properties by learning a sparse code for natural images［J］.Nature，1996，38(1):607 － 609.

［6］LEWICKI M S，SEJNOWSKI T J.Learning overcomplete representations［J］.Neural Computer，2000，12(2):337 －365.

［7］COMBETTESP，WAJSV.Signal recovery by proximal forward－ backward splitting［J］.SIAM Journal of Multiscale Model Simulation，2005(4):1168 －1200.

［8］CLARKE F.Optimization and nonsmooth analysis［M］.New York:Wiley Press，1983.

［9］CAND`ES E，ROMBERG J，TAO T.Stable signal recovery from incomplete and inaccurate information［J］.Communications on Pure and Applied Mathematics，2005，59(6):1207－1233.

［10］MILLER A.Subset selection in regression［M］.London:Chapman and Hall，2002.