与更新过程有关的几个概率分布及其数字特征*

姜培华，纪习习，吴 玲

(安徽工程大学 数理学院, 安徽 芜湖 241000)

与更新过程有关的几个概率分布及其数字特征*

姜培华，纪习习，吴 玲

(安徽工程大学 数理学院, 安徽 芜湖 241000)

对更新过程进行探讨，推导给出几个与更新过程有关的概率分布及其数字特征，进而将一般更新过程特殊化为齐次泊松过程，得出几个相应的推论.这些分布和推论在刻画城市交通流和行人流中都有重要应用.

更新过程；泊松过程；瓦尔德等式；数字特征

引言

1 预备知识与引理

定义1[1](更新过程) 设{Xn,n=1,2,…}是一列独立同分布的非负随机变量，它们的共同分布函数是F(x).如果视Xn为一个计数过程的第n-1个事件和第n个事件之间的时间间隔，则第n个事件的发生时间是

这里，S0=0.把由

N(t)=sup{n:Sn≤t}，N(0)=0,t≥0

定义的计数过程{N(t),t≥0}称作更新过程.为了避免显而易见的平凡情形，假设F(0)=P(Xn=0)lt;1，通常约定F(0)=0.

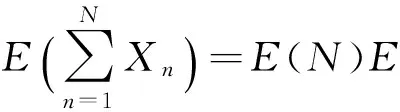
引理2[3]设X1,X2,…为独立同分布的随机变量序列，且方差存在.随机变量N只取整数值，Var(N)存在，且N与{Xn}独立，则：

2 主要结论及证明

定理1若{N(t),t≥0}为一更新过程，其更新时间间隔为Ti(i=1,2,…)，且Ti的密度函数为f(t)，分布函数为F(t),E(Ti)=μ,Var(Ti)=σ2，记Y为更新过程中首次出现更新间隔T≥t0的更新次数，则有：

1)Y服从参数为[1-F(t0)]的几何分布，即Y服从Ge(1-F(t0));

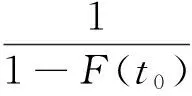
证明1)记T1是原点与第一次更新的时间间隔,Ti是指第i-1次更新与第i次更新的时间间隔，由更新间隔的独立性可知：

P(Y=h)=P(T1lt;t0,T2lt;t0,…,Th-1lt;t0,Th≥t0)=

P(T1lt;t0)P(T2lt;t0)…P(Th-1lt;t0)P(Th≥t0)=

[F(t0)]h-1[1-F(t0)]h=1,2,3,…

由几何分布的概率分布列定义可知,Y服从Ge(1-F(t0)).

2)由几何分布的期望、方差的计算公式易知

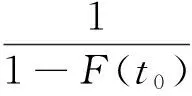
推论1 设Y为参数为λ的泊松过程中首次出现质点来到间隔T≥t0的质点个数, 则有：

1)Y服从参数为e-λt0的几何分布，即Y服从Ge(e-λt0);

2)EY=eλt0，VarY=(1-e-λt0)e2λt0.

证明利用定理1，取F(t0)=1-e-λt0，即可得证.

其中Fh(t)为F(t)的h重卷积，即Fh(t)=F*F*…*F，F为Ti的分布函数.

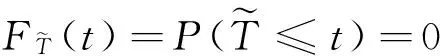
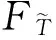
当tgt;0时，则：

其中Fh(t)为F(t)的h重卷积，即Fh(t)=F*F*…*F，F为Ti的分布函数.

2)由引理1可计算出平均等待时间为

此结果可以解释为, 更新平均间隔时间为μ.所以[E(Y)-1]次更新完成所需的平均时间为μ[E(Y)-1].

利用引理2可计算得到：

注：推论2中的结论1)与文献[4]中的定理2是一致的.

证明利用定理2，取F(t0)=1-e-λt0，E(Ti)=1/λ，Var(Ti)=1/λ2，即可得证.

定理3 在定理1条件下，设Z为更新过程中第r次出现更新间隔T≥t0的更新发生总次数, 则有：

1)Z服从参数为[r,1-F(t0)]的负二项分布，即Z服从NB(r,1-F(t0));

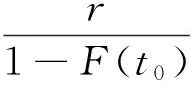
证明1)记T1是原点与第一次更新的时间间隔，Ti(i=1,2,…,z)为第i-1 次更新与第i次更新的时间间隔, 由相继更新间隔的独立性和负二项分布与几何分布的关系可知：

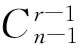
由负二项分布的概率分布列定义可知,Z服从NB(r,1-F(t0)).特别地当r=1时, 即是定理1 的情形.

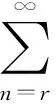
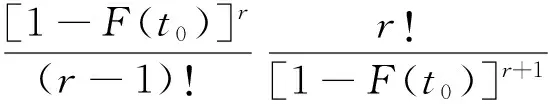
特别地, 当r=1时，即是E(Y).

因Z服从NB(r,1-F(t0))，由负二项分布与几何分布的关系可知：

推论3 设Z为参数为λ的泊松过程中第r次出现来到质点间隔T≥t0的质点发生总个数, 则有：

1)Z服从参数为(r,e-λt0)的负二项分布，即Z服从NB(r,e-λt0);

2)E(Z)=reλt0，Var(Z)=r(1-e-λt0)e2λt0.

证明利用定理3，取F(t0)=1-e-λt0，即可得证.

定理4 在定理1条件下，更新过程中出现第r次更新间隔Tr≥t0的平均等待时间为:

证明设出现第r次更新间隔Tr≥t0的等待时间为Wz-1，T1为原点与第一次更新的时间间隔，Ti(i=1,…,z-1)为第i-1次更新与第i次更新的时间间隔,则有：

Wz-1=T1+…+Tz-1

由于T1,…,Tz-1相互独立, 且E(Ti)=μ，又{Z-1=z}与Tz+1,Tz+2,…,独立，由引理1知：

推论4 若质点以强度为λ的泊松过程到来，出现第r个质点间隔Tr≥t0的平均等待时间为

注：推论4与文献[4]中的定理4本质上是一致的.

证明利用定理4，取F(t0)=1-e-λt0，E(Ti)=1/λ，即可得证.

3 结束语

随着经济社会的发展，城市建设也在不断发展，尤其是城市化步伐的加快使得城镇居民急剧增加，城市的车流量和人流量显著增加，因此城市交通路网规划和管理的科学化、现代化，前瞻化日趋迫切[5，6].对于城市交通中通过某交通路口的车流量一般可以近似用泊松过程来刻画，行人通过红绿灯路口的数量也可以用泊松过程来近似.文中第二部分推导给出的概率分布和结论在量化城市交通拥挤问题中都有诸多应用，如：行人需要等待多少车辆方可穿越人行横道？行人需要等待多长时间才能穿越人行横道？在给定的时间段内可以通过多少行人，行人有多少可以穿越的机会等等[4].

[1]王军，王娟. 随机过程及其在金融领域中的应用[M]. 北京：清华大学出版社, 2007.

[2] Ross S M. 随机过程[M]. 何声武，谢盛荣，程依明，等译.北京：中国统计出版社, 1997.

[3] 茆诗松，程依明, 濮晓龙. 概率论与数理统计教程[M]. 北京：高等教育出版社, 2011.

[4] 李泽慧. 与Poisson流有关的几个概率分布及其在城市交通拥挤问题中的应用[J].兰州大学学报：自然科学版，1984,20(数学专号)：127-136.

[5] 陆化普，王继峰，张永波. 城市交通规划中交通可达性模型及其应用[J].清华大学学报：自然科学版，2009,49(6)：765-769.

[6] 屠光启.加快改善宁波市区交通状况的建议[J].宁波经济丛刊，2004,(2)：46-48.

SomeProbabilityDistributionandItsNumerricalCharacteristicsAssociatedwithaRenewalProcess

JIANG Pei-hua，JI Xi-xi, WU Ling

(School of Mathematics and Physics, Anhui Polytechnic University, Wuhu Anhui 241000, China )

The renewal process is discussed, some probability distributions and its digital character associated with the renewal process are derived, then the general renewal process special into the homogeneous poisson process, several similar conclusions are given. These distributions and inferences have important applications in the characterization of city traffic flow and pedestrian flow.

renewal process; poisson process; Wald Equation; digital character

1673-2103(2013)05-0001-04

2013-10-02

国家自然科学基金资助项目(11226218)；安徽省自然科学基金资助项目(1208085QA04)；地方高校国家级大学生创新创业训练计划项目(201210363122)

姜培华(1979-)，男，山东曹县人，讲师，硕士，研究方向：概率统计和随机过程.

O212.1

A