跳出题海 “串”出实效:浅谈提升中考数学复习效率的策略

王振权

（珠海市斗门区第二中学，广东 珠海 519100）

复习课最重要的是帮助学生搭建知识网络，形成知识体系。因此，教师在课前要认真梳理教过的内容，提取主干知识，根据知识点前后的关系，把一个个知识点连接起来，形成知识的链接，横成串，竖成链。在课堂上，教师应从学生已有的知识和经验出发，运用各种教学策略，帮助学生构建知识网络,同时，教师要抓住生长点，适当拓展知识、深化知识，让学生觉得有新意，有新的收获。

近几年本地区的中考数学题安排了约80%的基础题，全卷的基础知识的覆盖面较广，许多试题源于课本，在课本中能找到原型，有的是对课本原型进行加工、组合、延伸和拓展。笔者认为教科书是中考题编写的源头，复习教学时我们要紧扣教材，夯实基础，可以把知识串一串，对典型问题、例题进行适当变式，达到举一反三、触类旁通的目的，提高学生的应变能力，从而提高中考数学复习的实效。

一、“串”知识点，让知识连成片

数学家华罗庚先生指出“学习有两个过程，一个是从薄到厚,一个是从厚到薄”,前者是“量”的积累，后者则是“质”的飞跃，教师在复习过程中，不仅应该要求学生对所学的知识、典型的例题进行反思，而且还应该重视对学生巩固所学的知识由“量”到“质”的飞跃这一转化过程。

例如，复习“直线、线段、射线”这一单元内容，笔者以表格的形式以一个基础、两个要点、三种延伸、四个异同点的复习提纲提出，激起学生学习的求知欲，学生思维活跃就会立即想方设法去寻找提纲的答案，在解决问题的同时，学生对本单元知识结构也就更加明晰。又如，在复习实际问题与一元二次方程时，笔者把它分成几种类型。A：握手问题（签合同、球类联赛、赠礼物等）；B：增长（下降）率问题；C：传播问题（分传播源重复传播、传播源不重复传播、传播源消失三类）；D：面积问题；E：经济生活问题；F：简单的综合题等。复习二次函数的知识点时，笔者把知识点以习题的形式出现。如“请研究二次函数y=x2-4x+3的图象及其性质，并尽可能多地写出有关结论”，通过这道题目的学习，学生已经基本上把二次函数的知识点都复习了一下。实践证明，这种把知识串联复习的方法使学生的知识更条理化、系统化，能把章节知识由量到质的飞跃，实现厚薄间的转化，确实能提升复习效率。

二、“串”典型图形，提高学习效益

现代学习理论的研究和大量的教学实践表明，人的学习过程是个体经验、知识和能力的构建过程；学生的认知不是一次完成而是在不断反复循环中实现的。

例如，在复习解直角三角形的时，笔者把典型的图形（如图 1、2、3）串在一起。

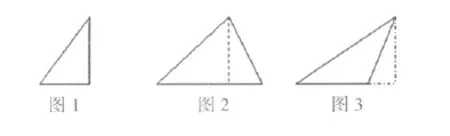
借助典型图形把解直角三角形中测量问题，航海问题等贯穿其中，达到知识的有效整合。

又如，在复习全等三角形时，笔者把两个全等的基本图形通过平移、翻折、旋转等变换，变成全等图形中典型的图形，再赋予具体的条件去解决问题，提升了复习的效率。因此，教学实践中，教师们在进行复习课教学设计时，所做的大量工作是把教材内容处理成更有利于学生学习的方式，学生的学习效益才会更高。

三、“串”试题的关联题，提升试卷讲评实效

特级教师吴正宪老师曾经打过比喻，知识犹如珍珠，如果不会整理，只是一盘散沙，没有太大的价值，只有穿成美丽的项链，才会价值连城。在复习阶段，反馈之一就是做往年的中考题，教师可以充分利用相关题，把题目作适当的串联，提高分析试卷的有效性。如，根据2011年珠海市中考数学题串联题目，已知：

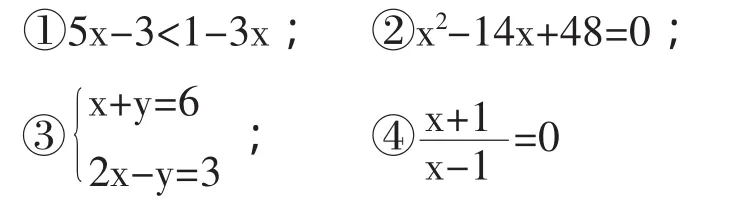
要求学生能准确的求方程（组）或不等式的解后，对原题作适当的变式。比如：若a为方程③的解，求a2-14a-1的值；若a为不等式④的解，求y=a2-4a-1的y取值范围；当x为何值时，直线y=5x-3总在y=1-3x的下方。

笔者认为，这样串题目讲评试卷，重在引导学生多总结方法，使学生做一题明一路。讲评试卷时以题带知识点，重在引导学生根据知识点的联系把它穿成线、连成片，编织成比较系统的知识网络。学生通过对问题的解决勾起对知识的回忆，对原题作简单的变式加深对知识的理解，从而提高复习的效率。

四、一题多变、一图多换——用变式教学提高教学效率

变式教学法，它的核心是利用构造一系列变式的方法，来展示知识发生、发展过程，数学问题的结构和演变过程，解决问题的思维过程，以及创设暴露思维障碍情境，从而形成一种思维训练的有效模式。它的主要作用在于凝聚学生的注意力，培养学生在相同条件下迁移、发散知识的能力。变式教学能激发学生的学习热情，能使学生尝试到成功的乐趣，达到解题举一反三、触类旁通的效果，能使学生的应变能力得以提高，进而提升复习的效率。笔者在复习课教学中尝试用变式教学的方法提高教学效率。

例如，已知点D、E、F分别是△ABC各边的中点，那么，当△ABC满足什么条件时，△DEF是等腰三角形？

变式1：（1）当△ABC满足什么条件时，△DEF是等边三角形？

（2）当△ABC满足什么条件时，△DEF是直角三角形?

（3）当△ABC满足什么条件时，△DEF是等腰直角三角形？

变式2：已知在四边形ABCD中点E、F、G、H分别是AB、BC、CD、DA各边的中点，请判断四边形EFGH的形状？当满足什么条件时，四边形EFGH是菱形？矩形？正方形？

本题的切入点较低，主要是应用三角形中位线定理和等腰三角形的定义，变式1和原题的难度没有差别，重在串知识点。变式2和原题相比难度有所提高，但第一问是书本的练习，把这些题通过变式的形式放在一起，由于结论的要求的不断变化，需要学生不能再机械地模仿，排除非本质特征的干扰，寻求解决问题的新途径。笔者在教学实践中发现，把这些题串在一起，对学生分析问题，解决能力的提高也大有帮助，特别对学生学会用三角形的中位线解决问题会有很大的帮助，

又如：在图4中，△ABC的边在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=PF．

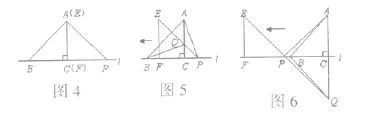
（1）在图4中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系。

（2）将△EFP沿直线l向左平移到图5的位置时，EP交AC于点Q，连结AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想。

（3）将△EFP沿直线l向左平移到图6的位置时，EP的延长线交AC的延长线于点Q，连结QP，BQ。你认为（2）中所猜想的BQ与QP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由。

该题是河北省的中考题，由于三角形EFP的平移，条件产生了变化，这就需要学生灵活运用所学的知识解决问题，问题解决的同时达到了变化中巩固知识、在运动中寻找规律、在知识纵横联系中提高学生灵活解题的能力。

笔者认为，复习课例题的选择，应选择能够反映大纲最主要、最基本的内容和要求，最有代表性的典型习题，多给学生思考的时间，让学生在实践中获得灵感，在交流中撞出智慧。对例题进行分析和解答时，要发挥例题以点带面的作用，有意识、有目的地在例题的基础上作系列的变化，挖掘和利用问题的潜在价值，实现复习知识从量到质的转变。

五、一题多解、多题同解——优化解题思路

华罗庚先生指出：“取法乎上得其中，取法乎中得其下。”在数学问题解决中，数学教师不能满足于只会做题，还应研究解题的方法；不仅要研究具体的解题方法，还要研究解题的思想方法和策略，这样，在数学问题解决中才能得心应手。在具体的教学实践中，我们有许多一题多解的题目，多让学生尝试一题多解，有利于引导学生沿着不同的途径去思考问题，产生多种解题思路，培养学生发散思维的能力。学生对多种解题方法比较，找出新颖、独特的最佳的解题方案，可优化解题思路，达到质的提高，从而优化复习的过程。

考查同一知识点，可以从不同的角度，采用不同的数学模型，作出多种不同的命题，教师在复习制定中选题时要善于引导学生将习题归类，集中精力解决同类问题中的本质问题，总结出解这一类问题的方法和规律。如:

（1）k取何值时对任意实数x，代数式x2+2x-k的值都大于0。

（2）k取何值时，方程x2+2x-k=0没有实数根。

（3）k为何值时，对任意实数x，不等式x2+2x-k＞0恒成立。

（4）k为何值时，函数y=x2+2x-k的图象全部在x轴的上方。

这四题的解法是一样的，笔者在教学实践中发现，在复习课时把各种形式向学生展示一下对学习困难的同学和学习中等的同学是大有帮助的。

又如在复习应用题时，可以选下列4个题目作为例题。

（1）甲乙两人同时从相距10000米的两地相对而行，甲骑自行车每分钟行70米，乙骑摩托车每分钟行180米，问经过几分钟，甲乙两人相遇？

（2）从A地到B地，汽车需8小时，拖拉机需10小时，两车同时从两地相向而行，几小时可以相遇？

（3）一项工程，甲队单独做需8天，乙队单独做需10天，两队合作需几天完成？

（4）一池水单开甲管需8小时可以注满，单开乙管需10小时可以注满，两管同时开放，几小时可以注满？

上述四道应用题，题目表达方式虽不同，有的看似行程问题，有的看似工程问题，但本质基本相同，数量关系、解答方法基本一样。这样的归类训练复习，学生通过分析异同，便能在平时的学习中注意做有心人。笔者在教学实践中发现，引导学生加强解题方法的积累和归纳，研究解题的思想方法和策略，这样就能在数学问题的解决中高屋建瓴，最终达到提升复习效率目的。

总之，在中考数学复习中，我们能更多地把视点放在通过学生的领悟和教师的讲评来达到知识的回顾、巩固、再学习、再认识的动态过程，而绝非仅仅是追求学习结果，多在学习策略、思考方法和探索途径上下功夫，那么，九年级数学复习中常遇到的题海无边与知识有限、题海无序与学生头脑中认知结构的有序这两对矛盾便可获得不同程度的缓解。只有真正地把数学知识化解到学生的思维和能力中，九年级复习才有“跳出题海”的希望，进而达到培养学生能力，提高学生数学素质的目的。

[1]盛秀永.中考数学复习策略及操作建议[J].数理化解题研究，2012（02）.

[2]程春霖.中考数学复习应注意的几个问题[J].中学数学，2012（02）.