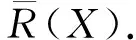关于IVF 近似空间的拓扑结构
喻光继
(广西财经学院信息与统计学院, 中国 南宁 530003)
粗糙集理论是著名科学家Pawlak在20世纪80年代初提出的一种处理模糊和不精确性问题的数学工具, 其对象的分类基于不可分辨关系(即等价关系). 经过二十多年的发展, 粗糙集理论巳成功地应用于数据挖掘、人工智能、决策管理、风险评估及故障诊断等多个领域[1-5].
粗糙集理论的核心概念是上、下近似运算, 它们是由一个论域上的等价关系导出的运算. 从拓扑学的角度看, 它们也可看作由一个论域上的等价关系所诱导出来的拓扑而产生的闭包算子和内部算子.
由于粗糙集和拓扑学都是基于集合论的, 它们之间存在密切、自然的联系. 讨论它们之间的关系, 有利于构建粗糙集理论的数学基础, 使拓扑学成为粗糙集理论的研究工具, 为拓扑学的实际应用开辟一条新途径. 本文研究了IVF二元关系与邻域算子, 获得IVF近似空间的拓扑结构,这不仅有助于理解粗糙集理论中的一些基本概念及其性质, 而且对拓扑学本身都具有理论和实际意义.
1 预备知识
本文涉及的粗糙集和拓扑学方面的概念和符号均参见文献[2, 6-9].
1.1 粗糙集
设U是称为论域的非空有限集,θ是U上的等价关系, 称序偶对(U,θ) 为近似空间.记U/θ为X上的由θ生成的等价类全体构成的集, 则U/θ中的元素称为基本集. 若将U的子集表示概念或知识, 则近似空间(U,θ) 称为知识结构. 基本集表示基本概念或知识模块. 可表示为若干个基本集的并的集合均称为可定义集, 否则称为不可定义集. 可定义集也称为精确集, 它表示已有知识, 它可在知识结构中被精确地定义或描述. 不可定义集也称为粗糙集, 它在知识结构中不能被精确地定义或描述, 但可用上近似集和下近似集来“近似”地描述.
1.2 区间值模糊集

定义1[10]设a,b∈[I],定义
(1)a=b⟺a-=b-,a+=b+.
(2)a≤b⟺a-≤b-,a+≤b+;a (3)aC=[1-a+,1-a-]. 定义2设a,b∈[I],定义 定义3[10]设ai∈[I](i∈J),定义 定义4[10]设U是论域,若A:U→[I]为映射,则称A为U上的区间模糊集(简称IVF集). 记F(i)(U)={A:A为U上的IVF集},F(i)(U×U)={A:A为U×U上的IVF集}.类似于模糊集,IVF集也有相应运算及运算律,这里省略. 定义5[10]∀A∈F(i)(U),x∈U,记A(x)=[A-(x),A+(x)],则分别称A-:U→I和A+:U→I为A的下模糊集和上模糊集. 定义6∀X∈2U,记 性质1设U是论域,且X,Y∈2U,则 证(1)∀x∈U, 由定义2得 而 (2)“⟹”设X⊆Y,∀x∈U, 由x∉Y得x∉X.于是U-Y⊆U-X.所以X⊆Y. (3)∀x∈U, 则 而 (4)类似(3)可证. 定义7若R∈F(i)(U×U),则称R为论域U上的IVF二元关系,称(U,R)为IVF近似空间。 定义8[11]设(U,R)是IVF近似空间,对任意x∈U,称 y→R(x,y) 为x的IVF邻域. 定义9[12]设(U,R)是IVF近似空间,则 性质2设(U,R)是IVF近似空间,则∀X,Y∈2U, 证(1)显然. (5)由(4)可得. 命题1设(U,R)是IVF近似空间,则以下条件等价. (1)R是自反的; (2)∀X∈2U,有R(X)⊆X; 则 因此R(X)⊆R(R(X)). 证由命题1和命题2可得. 定理1设(U,R)是IVF近似空间,且R为自反的,则τ={X∈2U:R(X)=X}是U上的拓扑. 证(i)由R为自反的,则由命题1,R()⊆.于是∈τ.由性质2(1),U∈τ. (ii)∀X,Y∈τ,由性质2(3),X∩Y∈τ. (iii)∀X,Y∈τ,由性质2(5),R(X∪Y)⊇R(X)∪R(Y)=X∪Y;由于R为自反的,则由命题1,R(X∪Y)⊆X∪Y.所以R(X∪Y)=X∪Y.于是X∪Y∈τ. 所以τ是U上的一个拓扑. 注3设(U,R)是IVF近似空间,且τ是U上的拓扑.记 intτ(X)=∪{Y∈τ:Y⊆X},clτ(X)=∩{Y∈τC:Y⊇X}. 其中τC={X∈2U:U-X∈τ}. 显然 intτ(U-X)=U-clτ(x);clτ(U-X)=U-intτ(X). (1) 定理2设(U,R)是IVF近似空间,R是自反的,且τ为定理1中的拓扑,则∀X∈2U, 证由性质2(4), intτ(X)=∪{Y∈τ:Y⊆X}=∪{R(Y):R(Y)=Y⊆X}⊆R(X). (2) 定理3设(U,R)是IVF近似空间,R是自反和传递的,且τ为定理1中的拓扑,σ={R(X):X∈2U},则 (1)τ=σ. 证(1)“⊆”设X∈τ,则X=R(X)∈δ.于是τ⊆δ. “⊇”设X∈δ,则存在Y∈2U使得X=R(Y).由推论1,R(R(Y))=R(Y).所以X=R(Y)∈δ.于是τ⊆δ. 因此τ=δ. (2)(a)“⊆”由定理2,intτ(X)⊆R(X). “⊇”类似(1)“⊇”可得R(X)∈τ.因R是自反的,由命题1得R(X)⊆X.于是 intτ(X)=∪{Y∈τ:Y⊆X}⊇∪{R(X)}=R(X). 所以intτ(X)=R(X). (b) 由(a)和性质2(2)可得. 参考文献: [1] PAWLAK Z. Rough sets[J]. Int J Comput Inform Sci, 1982,11(5):341-356. [2] PAWLAK Z. Rough sets: Theoretical aspects of reasoning about data [M]. Boston: Kluwer Academic Publishers, 1991. [3] PAWLAK Z, SKOWRON A. Rudiments of rough sets [J]. Inform Sci, 2007,177(1):3-27. [4] PAWLAK Z, SKOWRON A. Rough sets: some extensions [J]. Inform Sci, 2007,177(1):28-40. [5] PAWLAK Z, SKOWRON A. Rough sets and Boolean reasoning [J]. Inform Sci, 2007, 177(1):41-73. [6] YAO Y Y. Relational interpretations of neighborhood operators and rough set approximation operators [J]. Inform Sci, 1998,111(1-4):239-259. [7] SLOWINSKI R, VANDERPOOTEN D. A generalized definition of rough approximations based on similarity[J]. IEEE Trans Knowl Data Engin, 2000,12(2):331-336. [8] 张文修, 吴伟志, 梁吉业, 等. 粗糙集的理论与方法[M]. 北京:科学出版社, 2001. [9] ENGELKING R. General topology[M]. Warszawa: Polish Scientific Publishers, 1977. [10] CHENG Y, MIAO D. Rule extraction based on granulation order in interval-valued fuzzy information system [J]. Expert Sys Appl, 2011,38(10):12249-12261. [11] SUN B, GONG Z, CHEN D. Fuzzy rough set theory for interval-valued fuzzy information systems [J].Inform Sci, 2008,178(13):2794-2815. [12] 高宁华. 区间值模糊决策信息系统的属性约简及其相关问题[D]. 南宁:广西民族大学, 2013.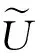


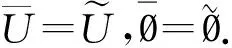
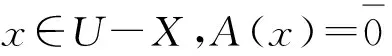

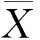
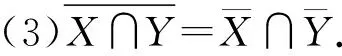






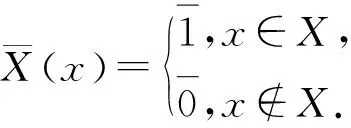
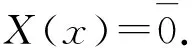


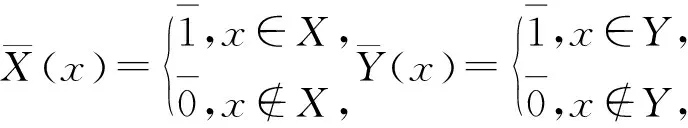


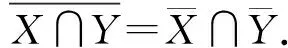
2 IVF二元关系
2.1 IVF二元关系与IVF邻域算子

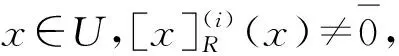
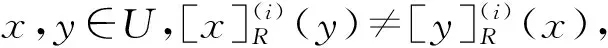


2.2 IVF二元关系与粗糙近似算子
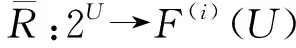




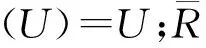
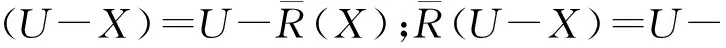
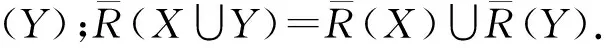



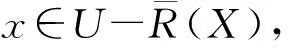
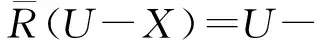








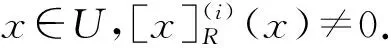
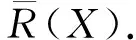
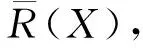
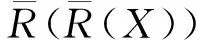


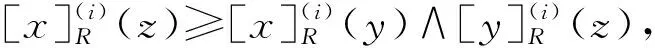

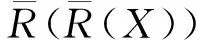

3 IVF近似空间的拓扑结构