一类基于开工时间恶化效应和基于位置学习效应的单机调度问题的求解
徐海燕
(金陵科技学院公共基础课部, 中国 南京 211169)
组合优化中有一类非常重要的问题就是排序,它广泛存在于生产调度、管理科学与工程、计算机科学与工程等众多领域中.经典的排序问题中工件的加工时间是一个固定不变的常数.但是,在某些实际生活中,工件的实际加工时间由于人的参与或者其他的原因会随着开始加工时间以及加工位置等不同而变化,这就是常常遇到的学习或恶化效应[1].
近年来,很多学者致力于调度问题中的学习效应和恶化效应的研究.Biskup[2]把学习效应模型分为基于时间和基于位置两种.基于位置的学习主要是由于处理某工件前的数量,而基于时间的学习主要是由于处理某工件前的工作时间.Biskup[3]首次把基于位置的学习效应引入到排序问题中,提出的学习函数为pir=pira,a<0,其中pir,pi分别表示被安排在r位置的工件i的实际加工时间和基本加工时间,并证明了在此模型下最小化总完工时间和具有一个公共的截止时间的总延误时间是多项式时间内可解的.类似地,Mosheiov[4-5]讨论了另外的一些单机调度问题和以目标函数为最小化总完工时间的并行机调度问题,Lee等[6]研究了同时考虑最小化总完工时间和总延迟时间的双目标问题在单机环境下的调度,Lee[7]提出了一个具有S型的学习函数的学习效应模型并在此模型下研究了一些调度问题.Kuo[8]首次提出了基于时间的学习效应模型.Koulamas和Kyparisis[9]介绍一个同时考虑基于位置和时间的学习效应模型.Cheng[10]等建立了一种基于工件被安排加工的位置和对数加工时间之和的学习效应模型,研究了在此模型下一些单机和多机的调度问题.Jiang[11]等研究了一种具有依赖工件开工时间的学习效应的单机调度问题.证明了在此模型下最小化总完工时间和最小化总加权完工时间和问题是NP-难的,并提出3类问题是多项式时间内可解的.Shen[12]等探讨了一种同时依赖时间和工件加工位置的学习效应的一般模型的单机调度问题.
除了上面考虑的学习效应,恶化效应广泛地存在于实际的调度中.Biskup[3]提出的学习函数为pir=pira,当a≥0时学习效应变为恶化效应[13].但是,文献中很少有学者同时考虑学习效应和恶化效应.Toksari和Guner[14]构造一个非线性混合整数规划模型来解决目标函数为最小化延误时间的并行机具有学习和恶化效应的调度问题. 在文献[15]中,作者提出了一种启发式方法来解决具有不同的释放时间的单机调度问题.在文献[16]中,作者提出了一些算法来解决具有基于时间的学习或恶化效应的单机调度问题.除了研究具有具体的学习函数的学习效应和恶化效应的模型之外,也有一些学者致力于研究通用函数的模型在单机调度中问题的求解[17].
基于位置的学习效应模型通常使用幂函数作为学习函数.但是Hurley[18]指出如果使用幂函数作为学习函数,当要被处理的工件的数量很大,按照幂函数的性质,处理工件的数量到一定时它的实际加工时间就接近于0了,这是不符合实际的.另外Lapre等人[19]研究得到学习函数该具有2种特性,其一,开始时为凹下降,其二到达一定时候不再变化或者变化很小.考虑到[18-19]所述内容,在Lee提出的具有学习效应的通用模型基础上[20],本文提出了一个同时具有学习和恶化效应的的通用模型,目标函数为极小化最大完工时间和最小化总完工时间,极小化延误时间,最小化总延误时间等问题,该模型具有更广的适用范围和实际意义.
1 问题描述

为了更好地表述,接下来给出一些符号说明:
对于一个调度序列π=(J1,J2,…,Jn),记:Cj=Cj(π)表示调度序列π中工件Jj的结束时间;Cmax=Cmax(π)=max{Cj(π)|j=1,2,…,n}表示序列π中的工件最大完工时间;∑Cj=∑Cj(π)表示序列π中工件完工时间之和;∑wjCj=∑wjCj(π)表示序列π中工件加权总完工时间和;Lmax=Lmax(π)=max{Cj(π)-dj|j=1,2,…,n}表示序列π中工件最大延迟时间;Tmax=Tmax(π)=max{0,Lj(π)|j=1,2,…,n}表示序列π中工件最大延误时间;∑Tj=∑Tj(π)表示序列π中工件延误时间和.
2 问题的求解
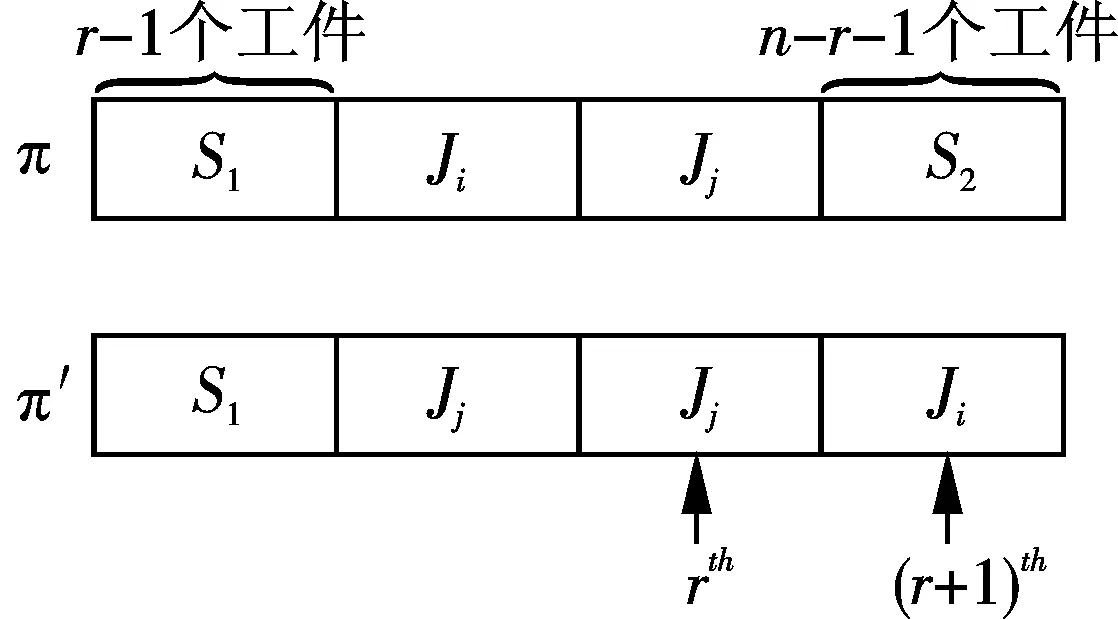
图1 交换相邻两个工件前后的调度序列对比Fig.1 A pairwise interchange of adjacent jobs
给出两个序列π=(S1,i,j,S2),π′=(S1,j,i,S2),其中Ji在序列π中位于第r个位置,Jj在序列π中位于第r+1个位置,同时Jj在序列π′中位于第r个位置,Ji在序列π′中位于第r+1个位置,S1中含有r-1个工件,S2中含有n-r-1个工件,如图1所示:
假设S1中所有工件完成操作的时间为t0,由此可以得到,序列π中Ji和Jj的完工时间为
相应地,序列π′中Ji和Jj的完工时间为
在这里,假设pi≤pj,为了方便描述,使用现在通用的Graham等[21]提出的三域表示法来描述调度问题.

证利用多元函数的偏导数的性质和中值定理显然可得.
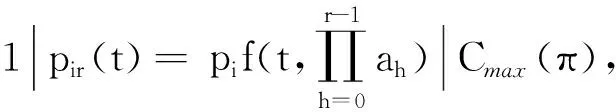
证先证明序列π=(S1,i,j,S2)优于π′=(S1,j,i,S2).分3部分证明.
1) 证明∀l∈S1,Cl(π)=Cl(π′).

由于S1中所有的工件都是一样的,所以∀l∈S1,Cl(π)=Cl(π′).
2) 证明Cj(π)≤Ci(π′).

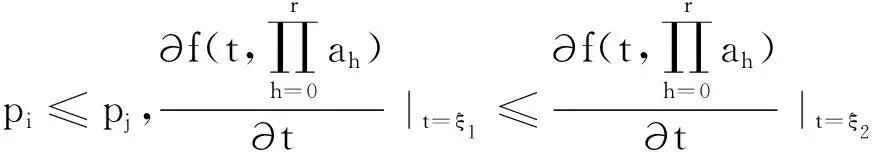
3) 证明∀l∈S2,Cl(π)≤Cl(π′).
假设l是S2中第1个工件,
由Cmax=max{Cj|j=1,2,…,n}得到序列π=(S1,i,j,S2)优于π′=(S1,j,i,S2),只要将工件按pi非减的顺序(SPT)排列得到的最优排序.

证由定理2可以得到结论.

证
∑wjCj(π′)-∑wjCj(π)=w1C1(π′)+…+wjCj(π′)+wiCi(π′)+…+wnCn(π′)-
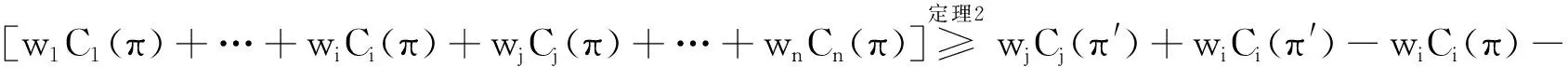
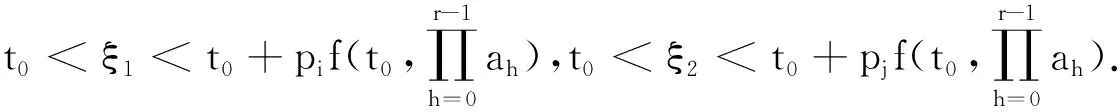
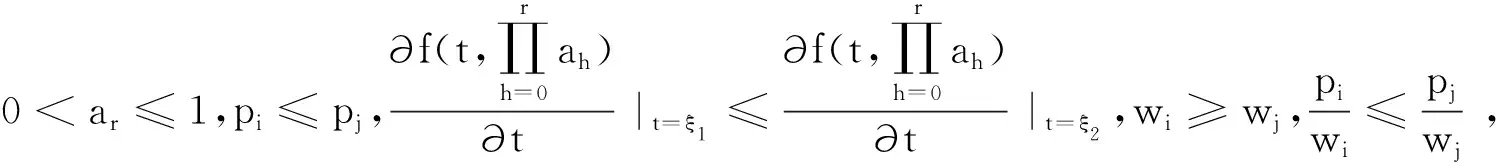
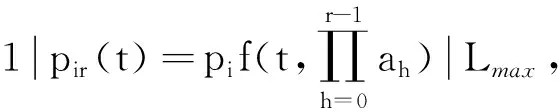
证因为Li(π)=Ci(π)-di,Lj(π)=Cj(π)-dj,Li(π′)=Ci(π′)-di,Lj(π′)=Cj(π′)-dj,
由pi≤pj,di≤dj以及Ci(π)≤Cj(π)≤Ci(π′)可知
Li(π)=Ci(π)-di≤Cj(π)-di≤Ci(π′)-di=Li(π′),Lj(π)=Cj(π)-dj≤Cj(π)-di≤
Ci(π′)-di=Li(π′),
max{Li(π),Lj(π)}≤Li(π′).
由于∀l∈S1,Cl(π)=Cl(π′),∀l∈S2,Cl(π)≤Cl(π′),可知
Lmax(π′)=max{L1(π′),…,Li(π′),Lj(π′),…,Ln(π′)}=
max{L1(π′),…,max{Li(π′),Lj(π′)},…,Ln(π′)}≥
max{L1(π),…,max{Li(π),Lj(π)},…,Ln(π)}=Lmax(π).
即序列π=(S1,i,j,S2)优于π′=(S1,j,i,S2),
因而只要将工件按非减顺序(EDD)排列即得到最优排序.

证
当Ci(π)-di≤0,Cj(π)-dj≤0时或者Ci(π)-di≥0,Cj(π)-dj≤0时或者当Ci(π)-di≤0,Cj(π)-dj≥0时,显然有:Ti(π′)+Tj(π′)-Ti(π)-Tj(π)≥0,当Ci(π)-di≥0,Cj(π)-dj≥0时,分两种情况讨论.

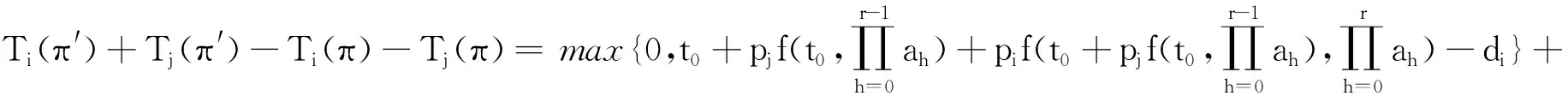
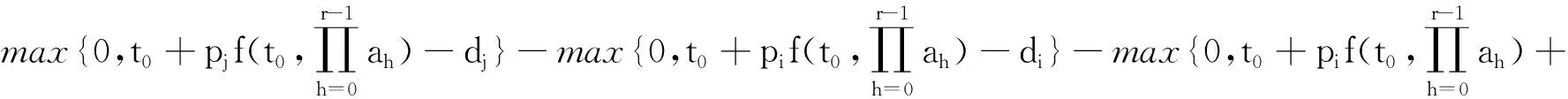
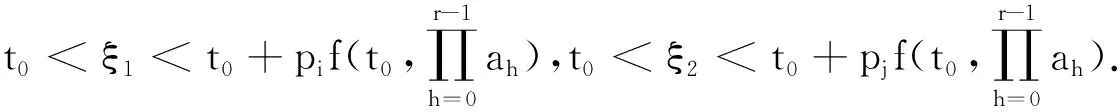
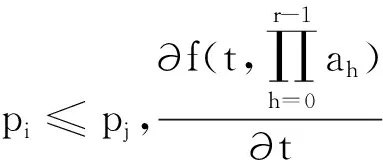

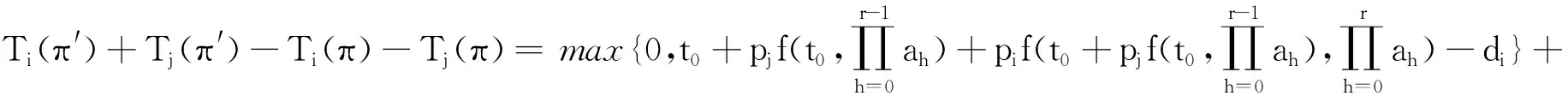
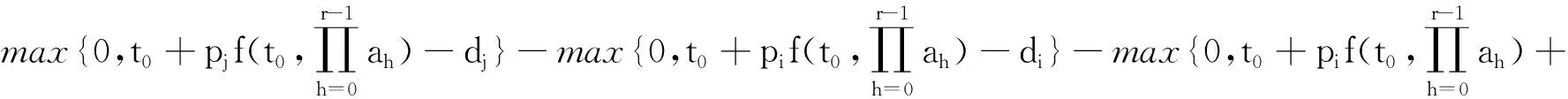
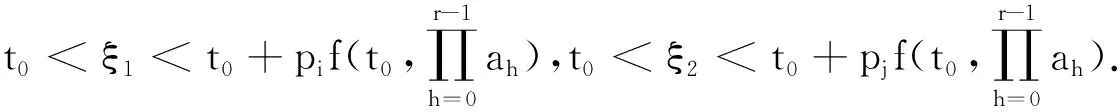
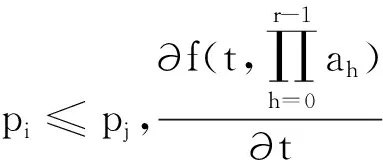
综上所述,序列π=(S1,i,j,S2)优于π′=(S1,j,i,S2),
故而只要将工件按di非减同时pi非减的顺序(EDD)排列即得到最优排序.
注定理2~6只是一个充分条件.


由于p2(=4)≤p3(=5)≤p1(=6),d2(=5)≤d3(=4)≤d1(=7),目标函数为Lmax,∑Ti的最优序列为[J2,J3,J1].
3 结论
近几十年来,很多学者研究具有学习函数或者恶化函数的模型,考虑到模型越是接近于实际,越是适用范围广,本文给出了一个具有一般性的函数模型,凡是满足此模型中的条件,都可以用该模型表示.作者在本文中将学习效应和恶化效应有效地结合在一起,研究了极小化最大完工时间、总完工时间和加权总完工时间、最大延误时间和总延误时间和在单机中的调度问题,证明了在某种情况下一些单机调度问题可以多项式可解.
参考文献:
[1] PINEDO M. Scheduling: theory, algorithms, and systems[M]. New York:Springer Science Business Media, 2012.
[2] BISKUP D. A state-of-the-art review on scheduling with learning effects[J]. Eur J Oper Res, 2008,188(2):315-329.
[3] BISKUP D. Single-machine scheduling with learning considerations[J].Eur J Oper Res, 1999,115(1):173-178.
[4] MOSHEIOV G. Scheduling problems with a learning effect[J]. Eur J Oper Res, 2001,132(3):687-693.
[5] MOSHEIOV G. Parallel machine scheduling with a learning effect[J]. J Oper Res Soc, 2001,52(10):1165-1169.
[6] LEE W C, WU C C, SUNG H J. A bi-criterion single-machine scheduling problem with learning considerations[J]. Acta Inform, 2004, 40(4):303-315.
[7] LEE W C. Scheduling with general position-based learning curves[J]. Inf Sci, 2011,181(24):5515-5522.
[8] KUO W H, YANG D L. Minimizing the total completion time in a single-machine scheduling problem with a time-dependent learning effect[J]. Eur J Oper Res, 2006,174(2):1184-1190.
[9] KOULAMAS C, KYPARISIS G J. Single-machine and two-machine flowshop scheduling with general learning functions[J]. Eur J Oper Res, 2007,178(2):402-407.
[10] CHENG T C E, KUO W H, YANG D L. Scheduling with a position-weighted learning effect based on sum-of-logarithm-processing-times and job position[J]. Inf Sci, 2012,221:490-500.
[11] JIANG Y Z, CHEN F F, KANG H Y. Single-machine scheduling problems with actual time-dependent and job-dependent learning effect[J]. Eur J Oper Res, 2013,227(1):76-80.
[12] SHEN L X, WU Y B. Single machine past-sequence-dependent delivery times scheduling with general position-dependent and time-dependent learning effects[J]. Appl Math Model, 2013,37:5444-5451.
[13] GORDON V S, POTTS C N, STRUSEVICH VA,etal. Single machine scheduling models with deterioration and learning: handling precedence constraints via priority generation[J].J Sched, 2008,11(5):357-370.
[14] TOKSARI M D, GUNER E. Minimizing the earliness/tardiness costs on parallel machine with learning effects and deteriorating jobs: a mixed nonlinear integer programming approach[J]. Int J Adv Manuf Tech, 2008,38(7-8):801-808.
[15] TOKSARI M D. A branch and bound algorithm for minimizing makespan on a single machine with unequal release times under learning effect and deteriorating jobs[J]. Comput Oper Res, 2011,38(9):1361-1365.
[16] QIAN J B, STEINER G. Fast algorithms for scheduling with learning effects and time-dependent processing times on a single machine[J]. Eur J Oper Res, 2012,225(3):547-551.
[17] WANG J B, HSU C J, YANG D L. Single-machine scheduling with effects of exponential learning and general deterioration[J]. Appl Math Model, 2013,37(4):2293-2299.
[18] HURLEY W J. When are we going to change the learning curve lecture? [J]. Comput Oper Res, 1996,23(5):509-511.
[19] LAPRE M A, MUKHERJEE A S, WASSENHOVE L N V. Behind the learning curve: Linking learning activities to waste reduction[J]. Man Sci, 2000,46(5):597-611.
[20] HUANG X, WANG J B, WANG L Y,etal. Single machine scheduling with time-dependent deterioration and exponential learning effect[J]. Comput Ind Eng, 2010,58(1):58-63.
[21] GRAHAM R L, LAWLER E L, LENSTRA J K,etal, Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Ann Discrete Math, 1979,5(2):287-326.

