峰谷时段划分对含电动汽车配电系统负荷曲线的影响
张振夫,凌生智
( 1.湖南省电力勘测设计院,中国 长沙 410082;2.湖南女子学院应用数学与智能信息处理研究所,中国 长沙 410004 )
人类正面临严重的环境与资源问题[1],随着政府的大力推动及相关技术的逐渐成熟,电动汽车的保有量在不断增长[2].不断增加的充电负荷在无序充电时可能将推高电网最大负荷,造成系统设备过载[3],引起供电能力不足等问题[4].
为了降低电动汽车充电对电网的不利影响,现有的研究已提出了多种优化充电方案[5-9],通过调整充电功率,充电时间来实现优化充电的目标.但是这些方案对通信、量测、控制系统提出了较高的要求,可行性较低.在中国电力市场高度管制的背景下,分时电价是一种较为可行的调节手段.文献[10]研究了峰时段及谷时段电价对含电动汽车配电系统负荷曲线的影响,但是没有考虑时段划分的问题.而为了制定合适的分时电价政策减轻车辆充电行为对电网的影响,首先需要确定合适的时段划分.因此有必要研究不同时段划分对含电动汽车的配电网负荷曲线的影响.
本文首先建立了电动汽车充电负荷模型,在此基础上构建了充电负荷的分时电价响应模型,研究了不同时段划分下电动汽车接入电网时,系统负荷曲线的变化规律.
1 配电系统负荷曲线及充电负荷计算
1.1 基本假设
为了方便计算充电负荷,作出如下假设:
(1)电动汽车电池容量为24 kW·h;
(2)每公里耗电量为0.15 kW·h;
(3)电动汽车每天只在家中充一次电;
(4)每次充电需将电池充至满电量;
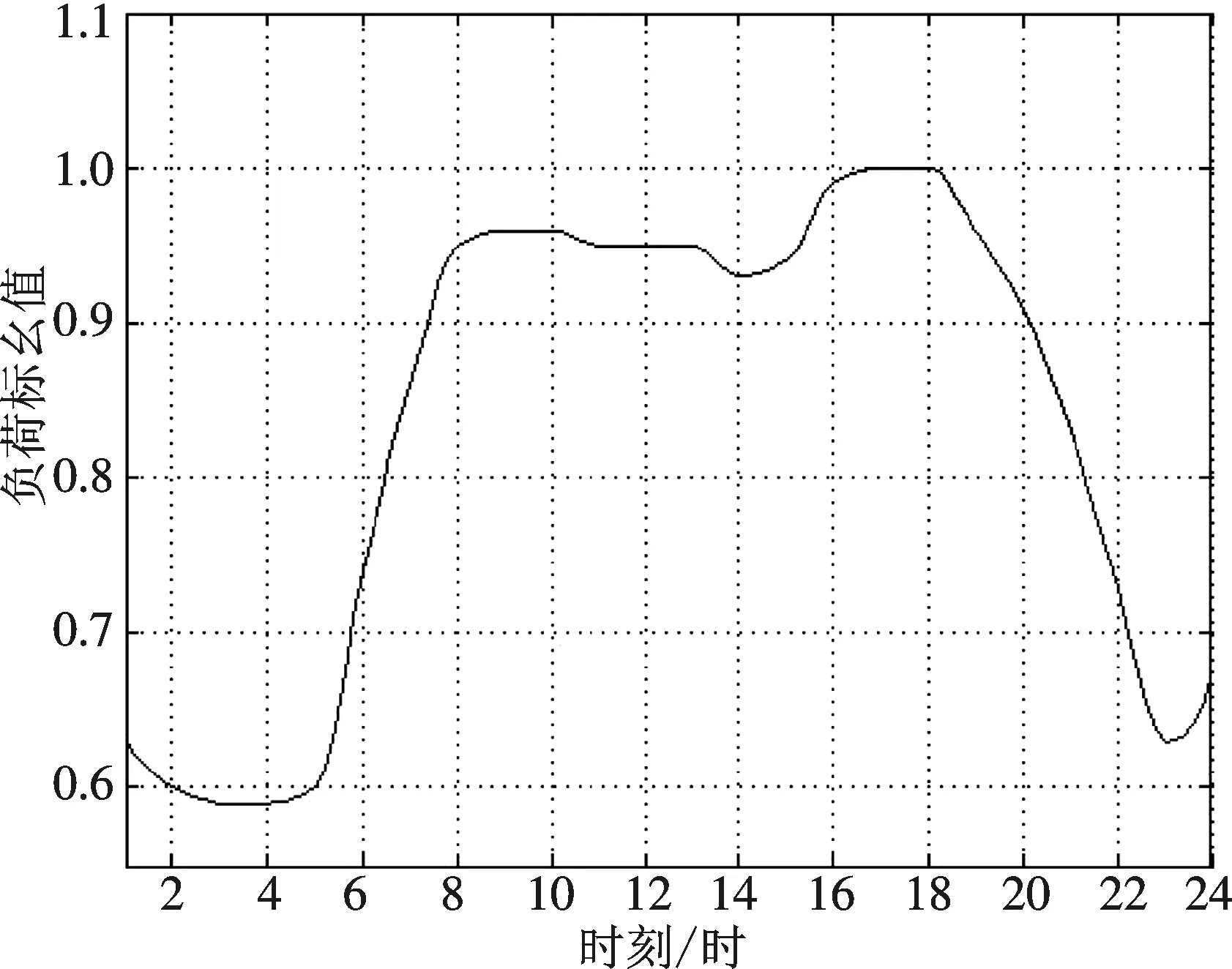
图1 配电系统负荷曲线Fig.1 Load curve of a distribution system
(5)电动汽车日行驶里程与行程结束时间是相互独立的随机变量.
1.2 配电系统负荷曲线
假设没有电动汽车接入时配电系统负荷xh服从正态分布[11],其概率密度函数如(1)式所示:
(1)
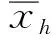
1.3 充电负荷计算
1.3.1 日行驶里程 根据驾车习惯的统计数据,电动汽车日行驶里程x近似满足对数正态分布[10],其概率密度函数如式(2)所示:

(2)
式中μD为期望值,μD=3.2;σD为标准差,σD=0.88.
1.3.2 行程结束时间 在到家即充电的模式下,电动汽车开始充电时间为行程结束时间.行程结束时间t近似满足正态分布[12],其概率密度函数如式(3)所示:
(3)
式中μS为行程结束时间期望值,μS=17.6;σS为标准差,σS=3.4.由于95%的车辆在上午10:00之后结束行程[13],为了简化分析过程,假设所有电动汽车均在上午10:00后结束行程.
1.3.3 充电方式 根据前面假设电动汽车在家充电,因此选择国家标准中充电方式1[14],其充电功率为4 kW.
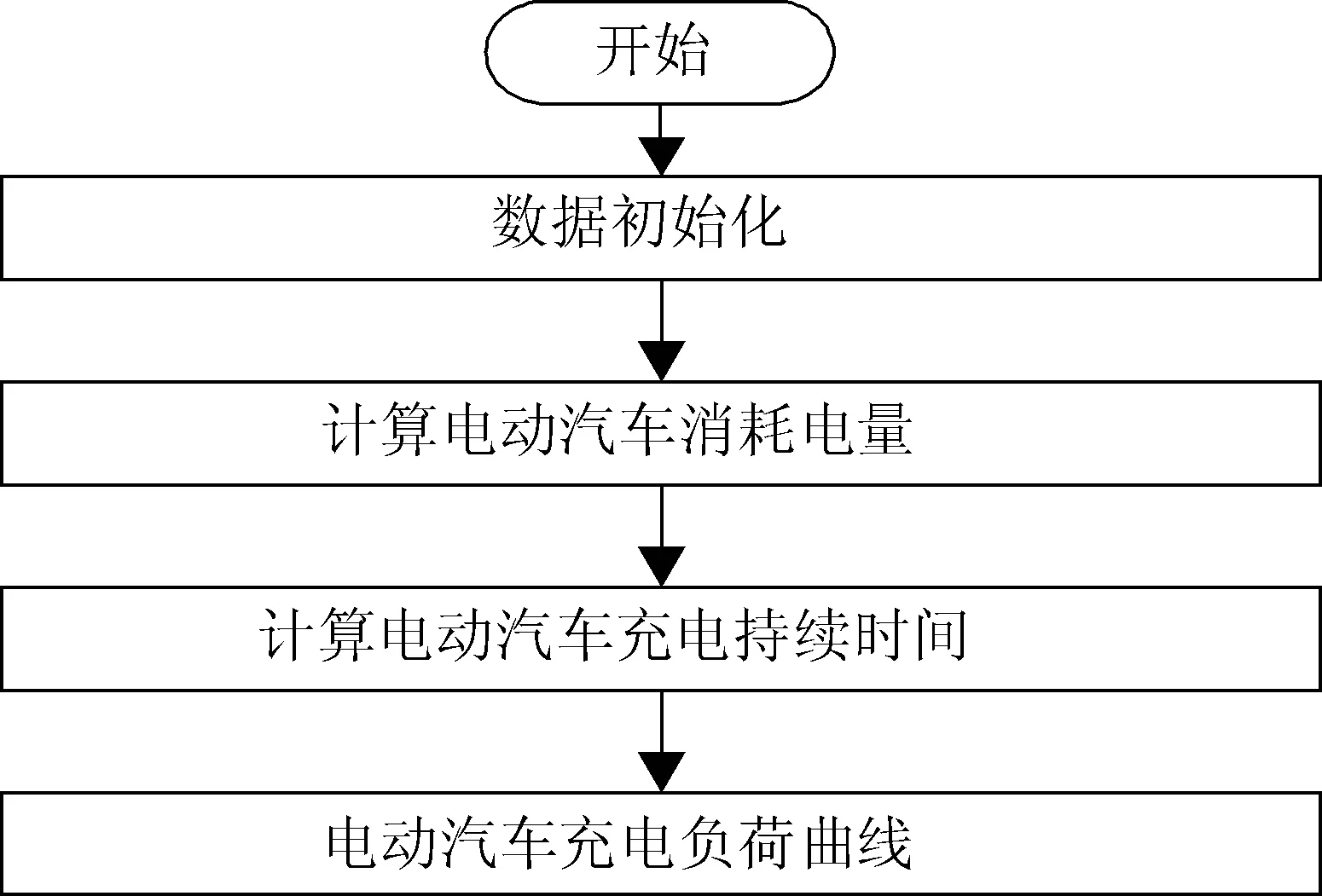
图2 单台电动汽车充电负荷计算流程图Fig.2 Flow chart of an EV charging load calculation
1.3.4 电动汽车充电负荷计算流程 单台电动汽车充电负荷计算流程如图2所示,具体过程如下:
(1)数据初始化:根据电动汽车日行驶里程概率密度函数产生随机数,得到该辆电动汽车的日行驶里程;根据行程结束时间的概率密度函数产生随机数,得到该车充电开始时间;
(2)计算电动汽车消耗电量:每公里耗电量乘以日行驶里程得到消耗电量;
(3)计算电动汽车充电持续时间:消耗电量除以额定的充电功率得到充电持续时间;
(4)得到电动汽车充电负荷曲线:根据充电开始时间,充电持续时间,充电功率得到单台电动汽车充电负荷曲线.
2 负荷对分时电价的响应
2.1 分时电价时段划分
电价因素对电动汽车充电负荷的影响较复杂,为了简化分析过程,本文主要考虑分时电价时段划分的影响而忽略电价的影响.目前已经实施的分时电价将全天分为峰时段,谷时段及平时段3段时间或者分为峰时段及谷时段两段时间.本文将全天分为峰时段及谷时段两段时间,T1为谷时段开始时刻.
2.2 电动汽车充电负荷对分时电价的响应
考虑到峰时段电价较高,谷时段电价较低,电动汽车将在谷时段充电以减少充电费用.因此电动汽车对分时电价的响应是电动汽车在到家后,改变开始充电时间,选择在谷时段充电.
在分时电价调节下,电动汽车充电负荷计算流程如图3所示,其中T1为荷谷开始时间,Ts为充电开始时间,Ta为行程结束时间,N为充电车辆数量.
首先根据驾车习惯的概率分布产生代表各辆电动汽车行程结束时间及日行驶距离的随机数.若电动汽车行程结束时间Ta在峰时段,出于充电费用最小的考虑,则该电动汽车将在谷时段开始时刻即T1时刻开始充电;当电动汽车行程结束时间在谷时段,则采取立即充电模式,即行程结束时间Ta为开始充电时间.然后采用前述方法计算每辆电动汽车的充电负荷.由于消耗电量及充电方式未发生变化,充电持续时间,充电功率等在考虑分时电价后仍然不变.将所有车辆的充电负荷曲线叠加,得到考虑分时电价时配电系统电动汽车充电负荷曲线.
图4为10 000辆电动汽车在没有分时电价调节时的负荷曲线,图5为谷时段开始时间为18:00,结束时间为6:00,10 000辆电动汽车的负荷曲线.由图可知,没有分时电价时,充电负荷在时间上分布较广,在考虑分时电价后,大部分电动汽车在谷时段开始充电,充电负荷集中分布于谷时段.当时段划分改变时,电动汽车充电负荷的响应与此类似.
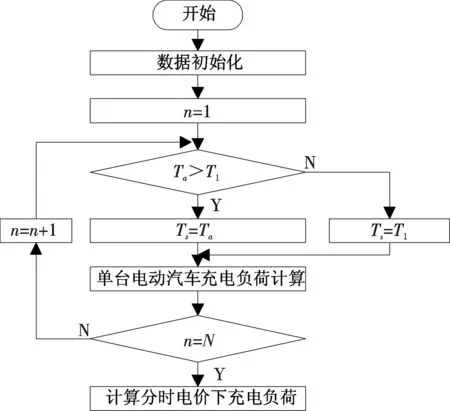
图3 考虑分时电价的充电负荷计算流程图Fig.3 Flow chart of charging load calculation with TOU

图4 无分时电价的充电负荷曲线Fig.4 Load curve of charging load without TOU
2.3 配电系统其他负荷对分时电价响应
电能是一种缺乏价格弹性的特殊商品[15],居民对电价的变化及不同时段划分响应较小.本文主要研究分时电价改变充电负荷分布后,充电负荷对系统负荷曲线的影响,因此忽略配电系统其他负荷对分时电价的响应,即根据前述方法得到其他负荷的负荷曲线后,在考虑分时电价时原负荷曲线仍保持不变.配电系统其他负荷的负荷曲线与考虑分时电价的配电系统充电负荷曲线相叠加可以得到考虑分时电价时配电系统的负荷曲线.
3 算例分析
3.1 场景设置与仿真流程
假设配电系统最大负荷为200 000 kW,负荷期望值标幺曲线如图5所示,系统中有 10 000辆电动汽车,电动汽车驾车习惯,充电行为遵循前述假设.为了研究不同时段划分对系统负荷曲线的影响,采用场景分析的方法,根据不同的时段划分设定多个相关场景.设场景1不考虑分时电价,电动汽车到家后即开始充电;另设定场景2至场景5共4个场景,其谷时段结束时刻均为早上6时,谷时段开始时刻分别为18时,20时,22时及24时.
仿真采用蒙特卡洛模拟的方法计算含电动汽车的配电系统负荷,为了减少随机性对仿真结果的影响,进行4 000次仿真,取其平均值.仿真流程如图6所示,先根据2.2节中的方法计算配电系统其他负荷的负荷曲线,然后分别计算前述5种场景下电动汽车的充电负荷,再将两者叠加后得到配电系统在各种场景下的负荷曲线,最后计算4 000次仿真中各时刻的负荷平均值.具体计算过程如前面章节所述.

图5 考虑分时电价的充电负荷曲线Fig.5 Load curve of charging load with TOU
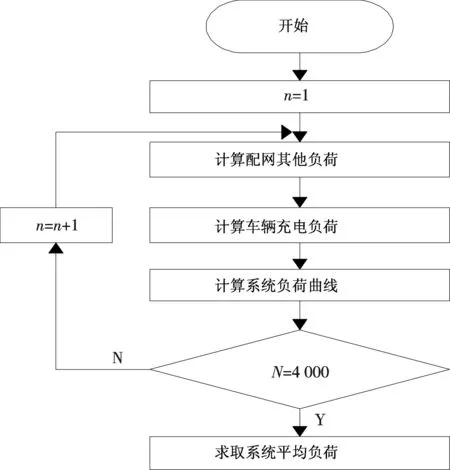
图6 仿真流程图Fig.6 Flow chart of simulation
3.2 仿真结果分析
在设置上述5个场景后,采用前述仿真方法从谷时段开始时刻系统负荷的变化,系统最大负荷的大小,出现时间及系统负荷峰谷差的变化4个方面研究时段划分对系统负荷曲线的影响.
场景1系统负荷曲线如图7所示.其他4个场景下,系统的负荷曲线如图8所示.由图可见,场景2至5中谷时段开始时刻的负荷与场景1中该时刻负荷相比,系统负荷有较大的增加.随着谷时段开始时刻越接近24点,该时刻负荷较场景一中相应时刻负荷增加越多.造成这一现象的原因是在谷时段之前到家的车辆集中于谷时段开始时刻充电,大量充电负荷聚集推高了该时刻系统的负荷.而随着谷时段开始时刻不断推后,同时充电的车辆也越多,负荷增加的幅值也越大.

图7 场景一系统负荷曲线Fig.7 Load curves of distribution system in scenario 1

图8 场景二至场景五系统负荷曲线Fig.8 Load curves of distribution system in scenario 2 to 5
尽管在场景2到场景5中谷时段开始时刻负荷较场景一有一定程度的增长,但是系统最大负荷出现时间却不一定在谷时段开始时刻.表1为5个场景下,系统的最大负荷大小及出现时间.从表中可见,未实施分时电价时,最大负荷出现在18时,在实施分时电价后,场景2与场景3下系统最大负荷出现时间与谷时段开始时间一致,而在之后两个场景中最大负荷出现在18时.因此当谷时段开始时间在深夜时,时段划分对最大负荷出现时间没有影响.而谷时段开始时间在傍晚时,改变了系统最大负荷的出现时间.
由于谷时段开始时间与配电系统中其他负荷的最大值出现时间相重合,此时刻的充电负荷与系统其他负荷叠加后,场景2的最大负荷较其他场景要高很多.在20时,系统其他负荷比18时要小,叠加充电负荷后,场景3与场景2相比其最大负荷要略小一些.场景4及场景5与其他场景相比,其最大负荷最小,等于系统中其他负荷的最大负荷.从上述分析可以看到,谷时段开始时间与系统其他负荷的最大负荷出现时间相距越远,时段划分对最大负荷的大小影响越小.
不同的时段划分对系统峰谷差有一定影响,各场景下系统的峰谷差如表2所示.
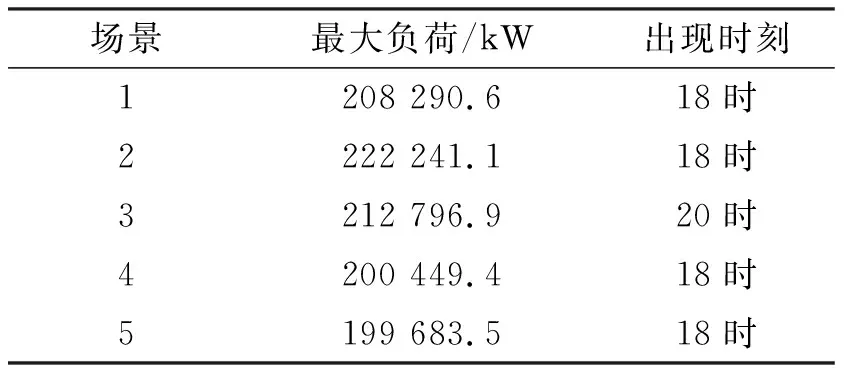
表1 不同场景下系统最大负荷及出现时间

表2 不同场景下系统峰谷差
从表中可知,场景1的峰谷差比场景2及场景3中的小,但是比场景4及场景5中峰谷差大,随着时段划分的推晚,峰谷差越来越小.在场景2中,由于系统中其他负荷的最大负荷与充电负荷叠加作用,使得接入电动汽车后系统最大负荷进一步增大,而最小负荷变化不大,系统峰谷差较其他场景要大.场景4与场景5中,时段划分较晚,与系统最小负荷时间接近,加入充电负荷后,系统最小负荷较其他场景有所增长,而最大负荷较其他场景要小,从而减小了系统峰谷差.因此谷时段开始时刻与最小负荷时刻越接近,系统负荷的峰谷差越小.
4 结论
(1)在实施分时电价后,谷时段开始时刻负荷较没有分时电价时系统负荷有所增长,且时段划分越晚,增长的幅度越大;
(2)谷时段开始时刻与系统其他负荷的最大负荷时刻相距越远,配电系统最大负荷数值越小,最大负荷出现时间与系统其他负荷的最大负荷时间一致;
(3)不同的时段划分将改变系统峰谷差大小,谷时段开始时刻与系统其他负荷的最小负荷时刻越接近,系统峰谷差越小;
(4)为了实现电动汽车有序充电,分时电价时段划分应考虑系统的负荷曲线特性,电动汽车数量等因素,谷时段开始时刻应远离系统最大负荷出现时间,接近最小负荷时刻,避免出现峰上加峰的现象.
参考文献:
[1] 毛六平,王耀南.混合动力汽车能源总成控制系统的研究[J]. 湖南师范大学自然科学学报, 2005,28(2):33-36.
[2] 朱 翔,蒲火元,苏 明.资源节约型与环境友好型视角下的县域经济竞争力综合评价研究[J].湖南师范大学自然科学学报, 2009,32(3):101-107.
[3] SHENGNAN S, PIPATTANASOMPOM M, RAHMAN S. Challenges of phev penetration to the residential distributio-n network[C]//Power and Energy Society General Meeting.Alberta,Canada:IEEE, 2009:1-8.
[4] 毛 弋,蒋 盈,李宝玉,等.多种通信方式并存的配网自动化通信系统的研究[J].湖南师范大学自然科学学报, 2013,36(4):31-36.
[5] CAO Y J, TANG S W, LI C B,etal. An optimized ev charging model considering tou price and soc curve[J].IEEE Trans Smart Grid, 2012,3(1):388-393.
[6] SANCHEZ-MARTIN P, SANCHEZ G, MORALES-ESPANA G. Direct load control decision model for aggregated ev charging points[J].IEEE Trans Power Syst, 2012,27(3):1577-1584.
[7] CLEMENT-NYNS K, HAESEN E,DRIESEN J. The impact of charging plug-In hybrid electric vehicles on a residential distribution grid[J].IEEE Trans Power Syst, 2010,25(1):371-380.
[8] SHENGNAN S, PIPATTANASOMPORN M, RAHMAN S. Demand response as a load shaping tool in an intelligent grid with electric vehicles[J].IEEE Trans Smart Grid, 2011,2(4):624-631.
[9] ZHANG P, QIAN K J, ZHOU C K. A methodology for optimization of power systems demand due to electric vehicle charging load[J].IEEE Trans Power Syst, 2012,27(3):1628-1636.
[10] SHAO S N, ZHANG T S, PIPATTANASOMPORN M. Impact of tou rates on distribution load shapes in a smart grid with phev penetration[C]//Transmission and Distribution Conference and Exposition.New Orleans,USA:IEEE ,2010:1-6.
[11] HATZIARGYRIOU N, KARAKATSANIS T, PAPADOPOULOS M. Probabilistic load flow in distribution systems containing dispersed wind power generation[J].IEEE Trans Power Syst, 1993,8(1):159-165.
[12] 田立亭,史双龙,贾 卓.电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010,34(11):126-130.
[13] 徐立中,杨光亚,许 昭,等.电动汽车充电负荷对丹麦配电系统的影响[J].电力系统自动化, 2011,35(14):18-23.
[14] 中国国家标准化管理委员会.GB/T20234.2-2011 电动汽车传导充电用连接装置第2部分:交流充电接口[S].北京:中国标准出版社,2011.
[15] 毛 弋,向海燕,康 伦,等.基于虚拟同步发电机的光伏并网系统及仿真分析[J].湖南师范大学自然科学学报, 2013,36(3):27-32.

