覆盖层次结构的知识距离刻画方法

宋晶晶, 杨习贝,2,3, 祁云嵩, 宋晓宁

(1. 江苏科技大学 计算机科学与工程学院, 江苏 镇江 212003) (2.南京理工大学 高维信息智能感知与系统教育部重点实验室, 江苏 南京 210094) (3.中国科学院 计算技术研究所智能信息处理重点实验室, 北京 100190)

粒计算最早是由美国控制论专家Zadeh提出的[1].粒计算是当前计算智能研究领域中模拟人类思维和解决复杂问题的新方法,它亦是复杂问题求解、海量数据挖掘、模糊信息处理的有效工具.文献[2]中首次提出了粒度的概念,立即引起了众多学者的广泛关注.

近年来,国内外关于粒计算的研究取得了重要进展.如文献[3]中为了体现粒计算思想的深度、广度及普适性,给出了粒计算三元论的概念,其主要成分是多视角、多层次粒结构和粒计算三角形;文献[4]中在集合论的框架下对粒计算进行了形式化的研究;文献[5]中研究了如何对复杂数据进行有效信息粒化以及利用信息粒化的结果进行高效问题求解;文献[6]中综述了粒计算的基本数学模型和方法,并讨论了它们之间的相互关系;文献[7]中探讨了基于粒计算的学习方法和应用前景.

就目前的研究成果来看,众多学者普遍认同这样一个观点:粒计算中的粒结构概念给出了一个系统或者问题的结构化描述.然而在实际工程应用中,对于同一个系统或者同一个问题,许多解释和描述可能是同时存在的[8],所以粒结构的形成常常需被模型化为多种层次结构.由此可以看出,层次性在粒计算中占据着重要作用.一般来说,粒结构层次化方法可以用于比较不同粒结构之间的粗细关系，如文献[9]中在不同知识粒度下,从属性变化的角度,给出了分层递阶的知识空间链.文献[10]中给出了邻域系统分层递阶结构的5条公理,提出了一种序关系来描述不同邻域系统之间的粗细关系.文献[11]中研究了两种多粒度空间下的分层递阶结构.文献[12]中从知识距离[13]的角度出发,研究了不同粒结构之间的差异.文献[14]中考虑了当信息粒之间不存在集合包含关系时,利用集合的基数大小关系来描述粒结构的层次性问题;文献[15]利用集合距离和知识距离构建了代数格结构,以此刻画基于等价关系信息粒的层次模型.

值得注意的是,以上众多学者对于粒计算层次结构的研究都是建立在等价关系基础上的，而在很多实际工程问题中,等价关系并不适用，如不同信息粒之间可能存在着重叠部分,此时所有的信息粒合集就构成了论域上的一个覆盖[16-17]而非划分.从这个角度来看,以粒计算的观点研究覆盖的层次结构是有实际意义的.文献[18]利用覆盖中信息粒之间的包含关系,定义了覆盖粒空间的层次模型.然而正如文献[14]中所指出的,在很多的复杂类型数据中,信息粒之间不存在必然的集合包含关系.为了解决这一问题,笔者在文献[15]的研究基础上,提出了覆盖上知识距离的概念,利用覆盖上知识距离格所诱导出的偏序关系来刻画覆盖的层次结构.

1 基本概念

1.1 粒结构

定义1令U≠∅为一论域,R为U上的一族等价关系的集合,称KB=为一个知识基[19].

给定一个知识基KB=,若P⊆R,则P中所有等价关系的交集依然是一个等价关系,Pawlak称其为不可分辨关系,记为IND(P)[19].以粒计算的观点来看,划分U/IND(P)中的每一个等价类就是一个信息粒,所有这些等价类的合集,也就是划分U/IND(P),就构成了一个粒结构.为后续讨论方便起见,不妨将由等价关系IND(P)生成的粒结构记为K(P)={[x]P:x∈U}[13],其中[x]P={y∈U: (x,y)∈IND(P)}表示U中所有与x具有等价关系IND(P)的对象的集合,即包含x的等价类.在论域U上, 将所有粒结构的合集记为K(U).

粒计算强调在不同粒度层次上来分析和解决问题,在粒计算理论中,有两种特殊的粒结构:一种是最粗的粒结构,记为σ={U:x∈U},此时根据二元关系,论域中任意两个对象都不能被区分开来,表示拥有的知识量达到最小;另一种是最细的粒空间,记为ω={{x}:x∈U}, 此时根据二元关系,论域中任意两个对象都可以被区分开来,表示拥有的知识量达到最大.

定义2[13]令U为论域,∀K(P),K(Q)∈K(U), 可定义如下所示的3种运算:

K(P)∩K(Q)={[x]P∩Q: [x]P∩Q=

[x]P∩[x]Q}

(1)

K(P)∪K(Q)={[x]P∪Q: [x]P∪Q=

[x]P∪[x]Q}

(2)

～K(P)={～[x]P: ～[x]P=

{x}∪(U-[x]P) }

(3)

定理1[13]令KB=为一知识基, (K(U),∩,∪)是一个格.

定理2[13]令KB=为一知识基,(K(U),∩,∪)是一个分配格.

定理3[13]令KB=为一知识基,(K(U),∩,∪,～)是一个有补格.

1.2 粒结构上的知识距离

定义3[12-13]令KB=为一知识基,∀K(P),K(Q)∈K(U),粒结构K(P)与K(Q)之间的距离称为知识距离,记为D(K(P),K(Q))且

D(K(P),K(Q))=

(4)

在定义3中, [x]P⨁[x]Q表示集合[x]P和[x]Q的对称差,即[x]P⨁[x]Q=([x]P-[x]Q)∪([x]Q-[x]P).D(K(P),K(Q))是用来度量两个不同单粒度空间所拥有知识含量差距的.显然, 0≤D(K(P),K(Q))≤1-1/|U|成立.当K(P)=K(Q), 即两个单粒度空间完全相同时,知识距离D(K(P),K(Q))达到最小值0; 当K(P)=～K(Q)时,知识距离D(K(P),K(Q))达到最大值1-1/|U|.

定理4[13]令KB=为一知识基,∀K(P),K(Q),K(R)∈K(U), 知识距离具有如下性质:

1) 非负性:D(K(P),K(Q))≥0,D(K(P),K(Q))=0当且仅当K(P)=K(Q);

2) 对称性:D(K(P),K(Q))=D(K(Q),K(P));

3) 三角不等式:

①D(K(P),K(Q))+D(K(P),K(R))≥D(K(Q),K(R))；

②D(K(R),K(Q))+D(K(P),K(R))≥D(K(Q),K(P))；

③D(K(R),K(Q))+D(K(P),K(Q))≥D(K(R),K(P)).

由定理4可知(K(U),D)是一个距离空间.

2 覆盖层次结构的距离刻画方法

2.1 覆盖与覆盖距离

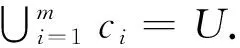
在此,称二元组(U,C)为一个覆盖近似空间.类似于粒结构的合集K(U), 由U上所有的覆盖构成的合集记为C(U).

从粒计算的角度看,覆盖的每个元素就是一个信息粒.在传统的粒结构讨论方法中,论域中的每一个对象仅仅属于一个信息粒的范畴,因而在考虑两个粒结构之间的知识距离时,只需求得对象在两个粒结构中信息粒的对称差即可.然而在覆盖中,∀x∈U,包含x的信息粒可能不止一个,简便起见,记覆盖C中包含x的信息粒的合集为C(x)={ci∈C:x∈ci}.此时要讨论两个不同覆盖之间的距离,首先需给出一个对象在两个不同覆盖之间的距离.

定义5令U≠∅为一论域, ∀x∈U,∀C1,C2∈C(U),x在覆盖C1与C2之间的距离有如下两种定义:

(5)

(6)

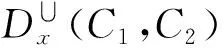
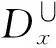
3)三角不等式:

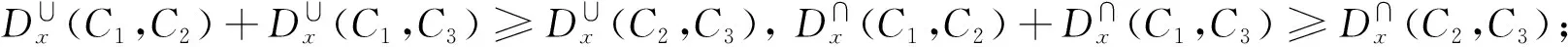
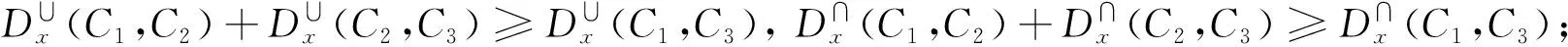
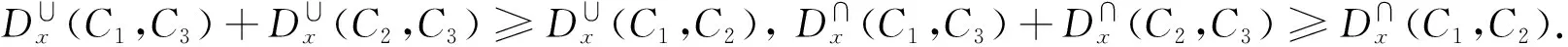
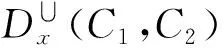
1)根据定义5, 非负性和对称性显然成立.

2)若覆盖C1,C2和C3中有两个覆盖相同,此时不妨假设C1=C2,根据定义5,3个三角不等式显然成立.

若C1,C2和C3两两都不相同,根据定义5,

由集合论的基本知识可知，对于任意有限集合X,Y和Z, 有(Y⨁Z)⊆(X⨁Y)∪(X⨁Z), 于是

类似地,不难证得其他三角不等式.

定义6令U≠∅为一论域, ∀x∈U,∀C1,C2∈C(U),覆盖C1和C2之间的距离有如下两种定义:

(7)

(8)

不难看出,D∪(C1,C2)是论域中所有对象在两个覆盖上并距离的平均值，而D∩(C1,C2)则是论域中所有对象在两个覆盖上交距离的平均值.

在定理5的基础上,同样可以得到如下所示的定理6.

定理6令U≠∅为一论域,∀C1,C2,C3∈C(U),覆盖之间的距离具有如下性质:

1)非负性:D∪(C1,C2)≥0,D∩(C1,C2)≥0;

2)对称性:D∪(C1,C2)=D∪(C2,C1),

D∩(C1,C2)=D∩(C2,C1);

3)三角不等式:

①D∪(C1,C2)+D∪(C1,C3)≥D∪(C2,C3),D∩(C1,C2)+D∩(C1,C3)≥D∩(C2,C3);

②D∪(C1,C2)+D∪(C2,C3)≥D∪(C1,C3),D∩(C1,C2)+D∩(C2,C3)≥D∩(C1,C3);

③D∪(C1,C3)+D∪(C2,C3)≥D∪(C1,C2),D∩(C1,C3)+D∩(C2,C3)≥D∩(C2,C3).

证明: 由定理5的证明结果,定理6易证.

2.2 覆盖上距离的代数结构

距离从几何角度刻画了不同粒结构或覆盖之间的几何结构,因而很自然地,可将两个粒空间或覆盖之间的关系通过距离反映出来.为此需选择一个参照空间,文中采用的是最细的粒空间,即ω.首先在覆盖上研究距离的代数结构,进而通过这个代数结构诱导出一个偏序关系,以此来反映覆盖之间的内在关系.

定义7令U≠∅为一论域,∀x∈U,∀C1,C2∈C(U),根据对象x在两个覆盖上的并距离,可定义如下两种运算形式:

(9)

(10)

根据对象x在两个覆盖上的交距离,可定义如下两种运算形式:

(11)

(12)

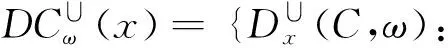
定理7令U≠∅为一论域,∀x∈U,

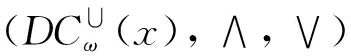
证明:根据定义7所示的最大最小运算,定理7易证.

2.3 覆盖上的层次结构

在一个格中, 可以根据“∧”与“∨”运算诱导出一种偏序关系.由定理7所示的格所诱导的偏序关系具体形式如定义8所示.

定义8令U≠∅为一论域,∀x∈U,∀C1,C2∈C(U),

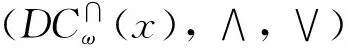
定义8所示的两种偏序关系可用于刻画覆盖上的层次结构,即∀C1,C2∈C(U).

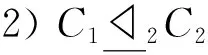
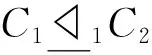
定理8令U≠∅为一论域,∀x∈U,∀C1,C2∈C(U),

|∪C2(x) |;

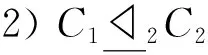
|∩C2(x) |.

证明: 仅证第1个结论,第2个结论的证明类似可得.

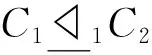
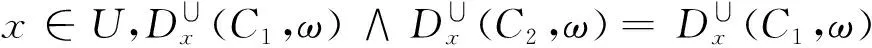
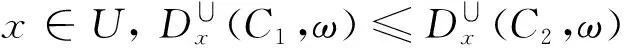
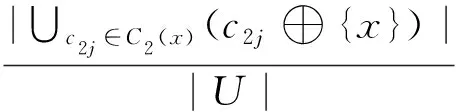
∀x∈U,|∪C1(x) |≤|∪C2(x) |.

例1:设论域U={x1,x2,x3,x4,x5,x6},C1,C2为论域U上的两个覆盖,其中

C1={{x1,x2,x4},{x2,x3,x5},{x4,x6},{x1,x2,x5}},

C2={{x1,x2,x3,x5},{x2,x5,x6},{x2,x3,x4,x5,x6}}.

根据定义5中式(5)得

根据定义5中式(6)得

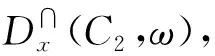
3 结论

粒计算中的粒结构是对一个问题的结构化描述,它的形成常常需被模型化为多种层次结构.根据实际问题求解的需要,选择相应层次的粒结构来解决问题.所以关于层次模型的研究对于粒计算理论的发展具有重要的现实意义.文中利用新给出的知识距离代数格所诱导出的偏序关系来刻画不同覆盖之间的粗细关系,通过实例分析说明这种方法是有效可行的.该方法为以后研究覆盖之间的层次结构提供了一种新的思路。

在文中工作的基础上,笔者下一步将对覆盖上基于知识距离的约简问题进行进一步的探讨.

参考文献(References)

[ 1 ] Zadeh L A. Fuzzy sets and information granulation[M].Amsterdam: North-Holland Publishing Company,1979: 111-127.

[ 2 ] Hobbs J R. Granularity[C]∥ProceedingsoftheNinthInternationalJointConferenceonArtificialIntelligence.California,Los Angeles：[s.n.],1985: 432-435.

[ 3 ] Yao Y Y. Granular computing: past,present and future[C]∥IEEEInternationalConferenceonGranularComputing.[S.l.]:Springer,2008: 80-85.

[ 4 ] 苗夺谦,徐菲菲,姚一豫,等. 粒计算的集合论描述[J]. 计算机学报,2012,35(2): 351-363.

Miao Duoqian,Xu Feifei,Yao Yiyu,et al. Set-theoretic formulation of granular computing[J].ChineseJournalofComputers,2012,35(2): 351-363. (in Chinese)

[ 5 ] 钱宇华. 复杂数据的粒化机理与数据建模[D]. 太原:山西大学,2011:17-56.

[ 6 ] 王国胤,张清华,胡军. 粒计算研究综述[J]. 智能系统学报,2007,2(6): 8-26.

Wang Guoyin,Zhang Qinghua,Hu Jun. An overview of granular computing[J].CAAITransactionsonIntelligentSystems,2007,2(6): 8-26. (in Chinese)

[ 7 ] Yager R R. Some learning paradigms for granular computing[C]∥IEEEInternationalConferenceonGranularComputing,[S.l.].IEEE,2006: 25-29.

[ 8 ] 王国胤,李德毅,姚一豫,等. 云模型与粒计算[M]. 北京: 科学出版社,2012: 139-140.

[ 9 ] 王国胤,张清华. 不同知识粒度下粗糙集的不确定性研究[J]. 计算机学报,2008,31(9): 1588-1598.

Wang Guoyin,Zhang Qinghua. Uncertainty of rough sets in different knowledge granularities[J].ChineseJournalofComputers,2008,31(9): 1588-1598. (in Chinese)

[10] 周君仪,杨习贝,杨静宇. 邻域系统分层递阶结构分析[J]. 计算机科学与探索,2012,6(3): 275-280.

Zhou Junyi,Yang Xibei,Yang Jingyu. Analysis of hierarchical structure of neighborhood systems[J].JournalofFrontiersofComputerScienceandTechnology,2012,6(3): 275-280. (in Chinese)

[11] Yang Xibei,Qian Yuhua,Yang Jingyu. Hierarchical structures on multigranulation spaces[J].JournalofComputerScienceandTechnology,2012,27(6): 1169-1183.

[12] Liang Jiye,Li Ru,Qian Yuhua. Distance: a more comprehensible perspective for measures in rough set theory[J].Knowledge-BasedSystems,2012,27: 126-136.

[13] Qian Yuhua,Liang Jiye,Dang Chuangyin. Knowledge structure,knowledge granulation and knowledge distance in a knowledge base[J].InternationalJournalofApproximateReasoning,2009,50(1): 174-188.

[14] Qian Yuhua,Dang Chuangyin,Liang Jiye. Partial ordering of information granulations: a further investigation[J].ExpertSystems,2012,29(1): 3-24.

[15] Yang Xibei,Qian Yuhua,Yang Jingyu. On characterizing hierarchies of granulation structures via distances[J].FundamentaInformaticae,2013,123(3): 365-380.

[16] Zhu William,Wang Feiyue. The fourth type of covering-based rough sets[J].InformationSciences,2012,201:80-92.

[17] Wang Lijuan,Yang Xibei,Yang Jingyu,et al. Relationships among generalized rough sets in six coverings and pure reflexive neighborhood system[J].InformationSciences,2012,207: 66-78.

[18] 胡军,王国胤. 覆盖粒度空间的层次模型[J]. 南京大学学报:自然科学版,2008,44(5): 551-558.

Hu Jun,Wang Guoyin. Hierarchical model of covering granular space[J].JournalofNanjingUniversity:NaturalSciencesEdition,2008,44(5): 551-558. (in Chinese)

[19] Pawlak Z. Rough sets: theoretical aspects of reasoning about data[M].Netherland:Kluwer Academic Publishers,1991:9.