FPSO系泊系统参数的动力效应影响分析

王志东, 刘晓健, 陈剑文

(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)

深水或超深水海上浮式生产储油船FPSO(floating production,storage and affcoading system)常采用张紧式系泊方式.在张紧式单点系泊系统中,转塔位置、系泊缆的布置与结构、系泊缆的材料参数都对FPSO的运动和缆绳张力产生影响[1].按照规范要求,极端海况下FPSO的水平偏移量应限制在水深的10%以内,系泊缆的安全系数应符合“动力法计算完整工况大于1.66,计算破损工况大于1.25”的要求[2].文献[3]中考虑长期环境荷载,开展了锚泊线的疲劳断裂研究,给出了不同材料、不同直径锚泊线的疲劳周期,为工程实用提供了借鉴.文献[4-5]中对16(4×4)根系泊线、12(4×3)根系泊线以及8(4×2)根系泊线4种系泊形式进行比较分析,在时域内开展了系泊线张力以及运动响应的分析研究.文中采用AQWA软件的时域计算功能,以FPSO水平偏移量(最大水平运动幅值)与系泊缆的安全系数(即系泊缆断裂强度/系泊缆最大张力)为优选目标,考虑系泊缆的非线性动态特性,通过时域耦合分析方法[6],对1 000 m水深的内转塔式FPSO单点系泊系统进行动力响应计算,研究侧风、顶浪、顶流海洋环境中系泊系统各项参数对FPSO系统动力效应的影响.

1 计算模型及环境条件

1.1 计算模型

文中选择FPSO的模型参数如表1.

表1 FPSO的设计参数Table 1 Design parameters of the FPSO

1.2 系泊系统模型参数

深水FPSO对系泊线的重量有一定限制,通常采用张紧式系泊方式[7].文中采用3×4分组布置的链-聚酯缆-链(其中钢链采用R4级无横档锚链)三成分锚泊线(共4组,每组3根,组与组之间90°平均分布,同组3根缆间角度为5°,每组3根缆的中间一根均沿着坐标轴)(图1).

参考API RP 2SM[8]及API RP 2SK[9]系泊系统设计规范,结合工程经验得知:一般情况下,为防止系泊线磨损和破坏,预张力控制在15%～30%断裂强度左右,顶部预张力张角一般控制在30°～50°.控制满载FPSO的水平偏移在10%的水深范围内,系泊缆的张力安全系数应满足“动力法计算完整工况大于1.66,计算破损工况大于1.25”的要求.且当张紧式锚泊线为三段式时,上下钢链的长度大约为全长的15%.因此，对锚泊系统参数进行初步设计如表2.

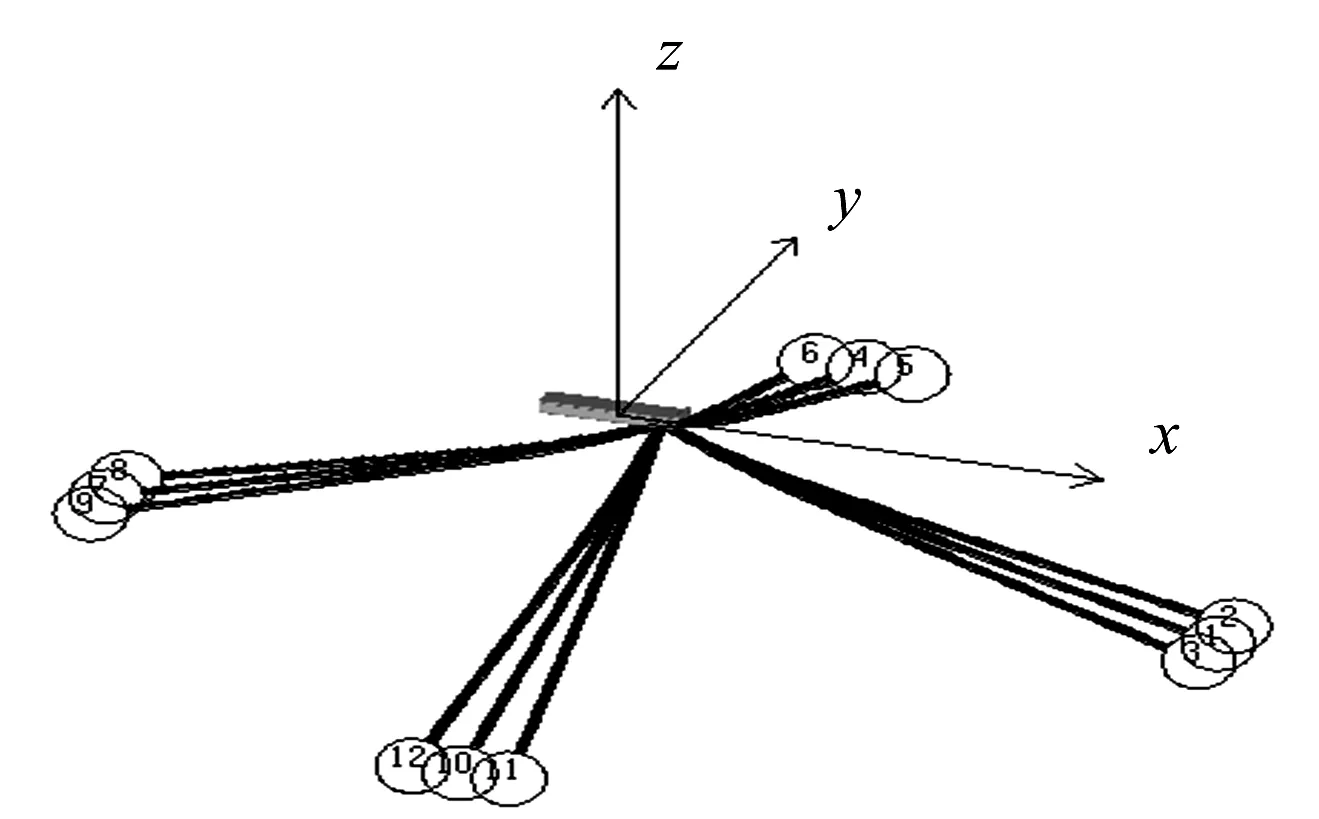
图1 FPSO系泊形式Fig.1 Mooring form of FPSO

表2 张紧式系泊系统参数Table 2 Taut-mooring system parameters

1.3 海洋环境条件

文中的FPSO以永久系泊于中国南海为目标,即在100年重现期有台风海况下,FPSO与单点系泊系统(SPM)不解脱,海洋环境条件见表3.

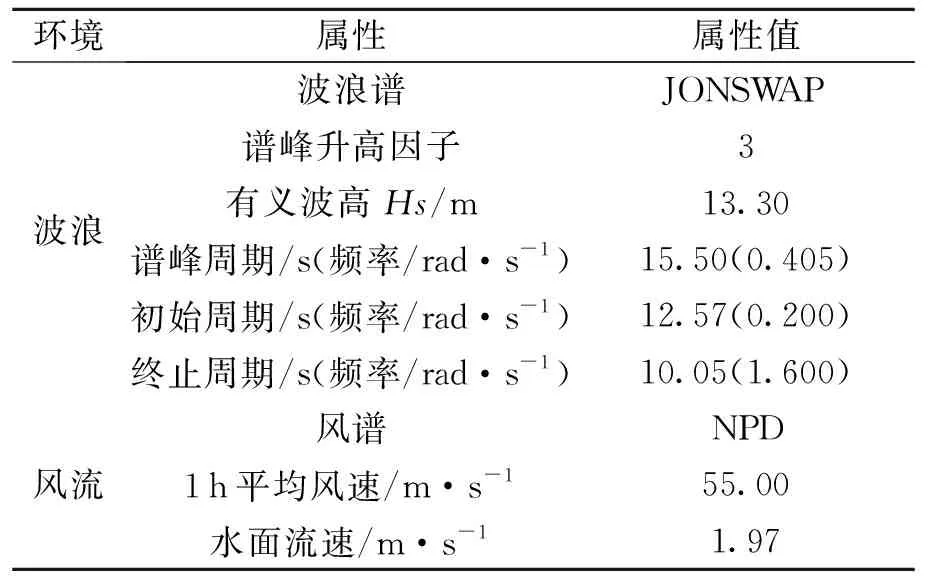
表3 中国南海百年一遇(台风)海洋环境[10]Table 3 Marine environment conditions in 100 years of South China Sea

2 系泊系统参数对FPSO系统动力效应的影响分析

2.1 不同内转塔位置对FPSO系统动力效应的影响

对于内转塔式单点系泊系统,转塔的位置是系泊系统设计中必须考虑的重要参数,其设计目标之一就是FPSO的风标效果[11].由于系泊缆与转塔相连,转塔越靠近船艏,缆绳垂向张力作用于FPSO上的纵摇力矩会越大,FPSO会产生埋首现象,需要将船舶的重心后移才能保持静水中FPSO的甲板水平.原则上内转塔装置可以布置在船头和船中之间的任何位置上,下面即对不同转塔位置(转塔分别距船艏柱7%，18%，25%，35%船长)的工况进行计算,比较分析FPSO 的艏摇运动、水平偏移及系泊张力.

表4给出了考虑重心位置变化下不同转塔位置时FPSO在侧风、顶浪、顶流环境中运动到平衡位置后,在平衡位置附近往复艏摇偏移的统计值.

表4 不同转塔位置FPSO艏摇运动计算统计值 (考虑重心调节)Table 4 Statistic value of yaw motion in different turret locations of FPSO

注：a为转塔距船艏柱距离；Lpp为垂线间长

从表4可以看出,转塔离船艏过近或过远,风标效果都不佳,转塔位置从距艏柱7%Lpp到25%Lpp,艏摇标准差缓慢减小,转塔位置从距艏柱25%Lpp到35%Lpp,艏摇标准差有所增大,文中所计算的4种转塔位置中,距船艏柱25%Lpp时风标效应最好.转塔离船艏过远(即离船中较近),转塔离FPSO重心较近,此时FPSO很难随着环境载荷的方向而改变艏向.而转塔离船艏过近,风标效果也较差的原因是,为保持系统整体的平衡,转塔过于靠近船艏,船舶自身的重心就会离船艉很近,重力的等效作用点与系泊力的等效作用点之间的距离会很大,从而导致系泊力的微弱变化都会引起FPSO的运动.

表5给出了不同转塔位置时FPSO在侧风、顶浪、顶流环境中水平偏移以及缆绳动张力的统计值.

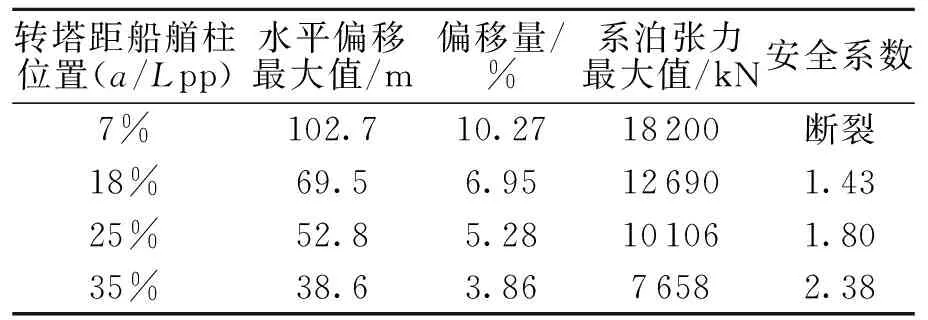
表5 不同转塔位置FPSO水平偏移及动张力计算 统计值(考虑重心调节)Table 5 Statistic value of the horizontal motion and mooring tension in different turret locations of FPSO

注:表中安全系数为系泊缆断裂强度/某工况下系泊张力的最大值，当系泊张力最大值大于系泊缆断裂强度时即断定缆绳断裂.

结果表明:系泊缆从船中靠近船艏时FPSO的水平偏移量增大,系泊链上部的垂直运动增加,导致系泊链的动张力增加,安全系数降低.综合考虑各方面因素,本文中转塔位置距船艏柱25%Lpp相对更为合理.

2.2 系泊缆材料分布对FPSO系统动力效应的影响

根据工程实践经验,三段张紧式锚泊线一般设计为上下钢链的长度大约为全长的15%,可根据实际情况进行调整.初步设计锚泊系统时,转塔位置距艏柱18%Lpp,在此基础上改变三段张紧式系泊缆每段的长度,比较分析其对FPSO系统动力响应的影响,以下针对钢链占缆长比例k1为10%,15%,20%3种情况进行计算,每种情况又分为上端钢链占钢链总长的10%,30%,50%,70%,90%5种工况,共15种工况比较分析.

表6及图2，3给出了系泊缆不同成分分布时FPSO在侧风、顶浪、顶流环境中水平偏移以及缆绳动张力的时域统计值.

表6 不同系泊缆材料分布下FPSO水平偏移及动张力计算统计值Table 6 Statistic value of the horizontal motion and mooring tension of FPSO under different mooring line material disthbutions

结果表明,“钢链-聚酯缆-钢链”三段式张紧式系泊缆中钢链越长,系泊系统的安全系数越高,但是同时FPSO的水平偏移量也越大.如果钢链的长度一定,接近锚点的下端钢链越长,系泊系统的安全系数n越高,且FPSO的水平偏移量δ也随下端锚链的增加而变小,当下端锚链占锚链总长比例k2为70%时偏移量最小,若下端锚链继续增加,则水平偏移量会有微量增加.

减小锚链长度虽能提高安全系数,但FPSO的水平偏移会偏大,且上端锚链的存在可避免缆绳与导缆器发生摩擦碰撞,下端锚链的存在可减小缆绳对锚的上拔力,提升定位质量.以上计算的15种系泊缆材料分布工况,水平偏移量均符合规范要求,

图2 不同系泊缆材料分布下FPSO水平偏移量Fig.2 Horizontal motion of FPSO under different mooring line material distributions

2.3 系泊缆预张力对FPSO系统动力效应的影响

缆绳顶部预张力的考虑主要集中在预张力大小与预张力倾角两个方面,给缆绳施加预张力是为了提供足够的初始刚度,使系统具有足够的恢复刚度以控制FPSO活动范围,但是预张力过大也会使系泊系统的安全系数偏小,顶部预张力倾角随水深的变化有所不同,一般控制在30°～50°比较合适,水深越深张力倾角越大.

由于改变系泊缆预张力及其倾角的因素很多,包括系泊缆材料、系泊缆各材料分布、系泊半径、缆绳长度等.以下考虑仅改变系泊缆的系泊半径和缆长来控制预张力及其倾角的变化,在上节计算的15种系泊缆分布工况中,选择下端钢链9%-聚酯缆90%-上端钢链1%的工况作为本节计算的基础,从而讨论张力及张力倾角对水平偏移、缆动张力的影响.

2.3.1 系泊缆预张力倾角对FPSO系统动力效应的影响

前面提到“一般来说预张力控制在15%～30%断裂强度左右”,但文中水深较深,缆绳长度较长,根据前期计算得知预张力太大,对缆绳的安全系数不利,所以为研究方便,在经验基础上做了适当的减小.利用控制变量方法,保证预张力为2 276 kN不变(约为断裂强度的12.5%),改变预张力倾角分析不同张力倾角下FPSO的水平偏移及缆动张力统计值的变化规律.

表7和图4,5给出了系泊缆预张力倾角α从25.0°变化到33.0°,FPSO水平偏移量δ及系泊缆动张力σ的时域计算统计结果.

随着张力倾角α的增大,FPSO的偏移量减小,但与此同时系泊系统的安全系数n也随之减小.在以上计算的8种工况中,水平偏移量δ均满足要求，

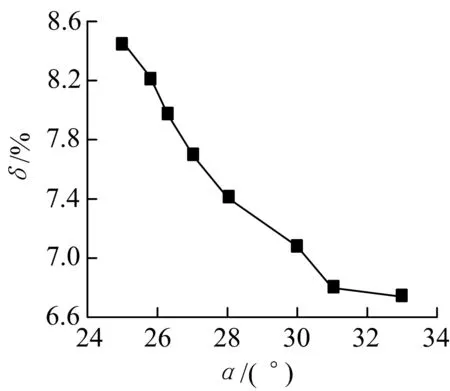
图4 不同预张力倾角下FPSO水平偏移量Fig.4 Horizontal motion of FPSO under different pre-tention angles

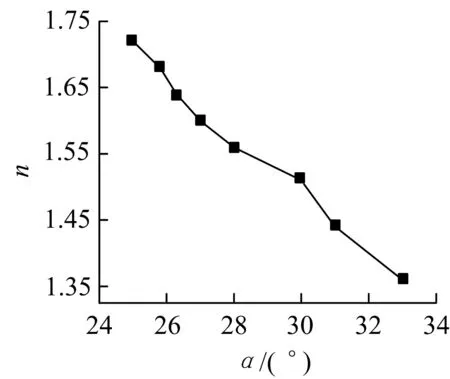
图5 不同预张力倾角下系泊缆安全系数Fig.5 Safety factor of mooring lines under different pre-tension angles

系泊缆安全系数只有在预张力倾角为25°及25.8°两种工况下符合要求.

2.3.2 系泊缆预张力σ对FPSO系统动力效应的影响

利用控制变量方法,当预张力倾角α为30°时,通过改变预张力σ的大小分析不同预张力情况下FPSO的水平偏移及缆动张力的统计值变化规律.

表8和图6,7给出了系泊缆预张力从1 310 kN变化到5 007 kN,FPSO水平偏移及系泊缆动张力的时域计算统计结果.

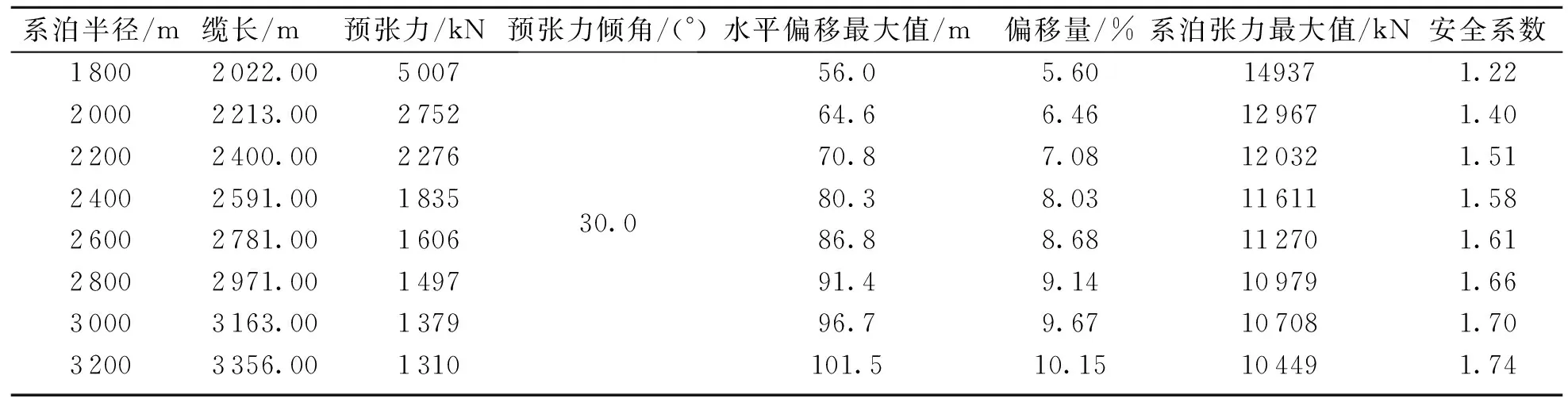
表8 不同张力下FPSO水平偏移及动张力计算统计值Table 8 Statistic value of the horizontal motion and mooring tension under different tention

图6 不同预张力下FPSO水平偏移量Fig.6 Horizontal motion of FPSO under different pre-tension

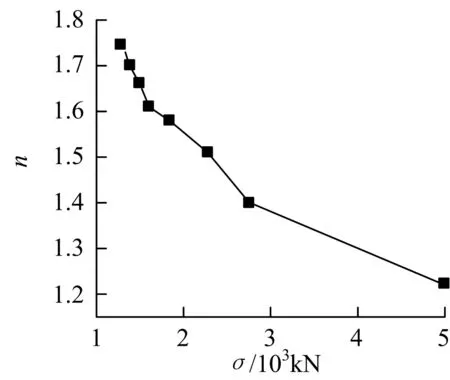
图7 不同预张力下系泊缆安全系数Fig.7 Safety factor of mooring lines under different pre-tention

FPSO的偏移量δ随着预张力σ的增大而减小,但同时系泊系统的安全系数n也减小.以上计算的8种工况中,前7种工况下的水平偏移量都满足要求,当预张力为1 310 kN时FPSO的水平偏移量偏大,超过了规范要求.只有预张力为1 310，1 379，1 497 kN时3种工况下系泊缆安全系数符合要求.

与半潜式系泊平台的多点散射系泊形式相比,单点系泊系统若要达到足够的安全系数,系泊半径与系泊缆长度均比多点散射系泊系统的更长.系泊缆的预张力/预张力倾角过小会导致FPSO的偏移量超过规范要求,且随着预张力/预张力倾角的减小,系泊半径越来越大,靠帮补给和外输作业都会受到系泊半径的影响,系泊半径过大会对FPSO的周边结构造成影响,同时预张力/预张力倾角减小时系泊缆长也会越来越大,过长的系泊缆会导致FPSO载重量减小,也会造成垂荡运动的变化影响系统的经济型;预张力/预张力倾角过大会导致缆张力增大,系泊系统的安全系数偏低.

2.4 系泊缆布置对FPSO系统动力效应的影响

2.4.1 系泊缆分布形式对FPSO系统动力效应的影响

对于转塔式系泊系统系泊缆的空间布置,可以采用两种模式[12]:组式系泊模式(图8)和平均散射系泊模式(图9),两幅图中分别包括船头方向有缆和船头方向无缆两种形式,组式系泊也要考虑缆分为几组、每组几根、每根之间的角度是多少等问题.由于任何一个因素的改变都会导致FPSO系统的动力响应发生变化,因此本条内容主要为:确定系泊缆为12根不变,讨论系泊缆为平均散射形式、3组×4根/组形式(每组缆间夹角120°,同组间缆夹角5°)、4组×3根/组形式(每组缆间夹角90°,同组间缆夹角5°)3种情况,每组情况中又讨论船长方向上有无系泊缆,每种工况下的缆绳都沿着船长对称,共6种工况下FPSO的水平偏移及缆动张力的统计值变化规律.在上节16种系泊缆预张力工况中,选择系泊半径2 800 m，缆长2 971 m，预张力1 497 kN,预张力倾角30°的工况作为计算基础.

表9为4种组式系泊模式以及2种平均散射系泊模式下的水平偏移及系泊缆动张力的时域计算,并给出了计算统计结果.

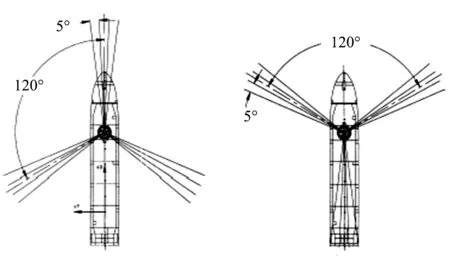
图8 组式系泊模式Fig.8 Grouped mooring mode

图9 平均散射系泊模式Fig.9 Equally spread mooring mode表9 不同系泊缆布置形式下FPSO水平偏移及动张力计算统计值Table 9 Statistic value of the horizontal motion and mooring tension under different arrangement forms of mooring lines

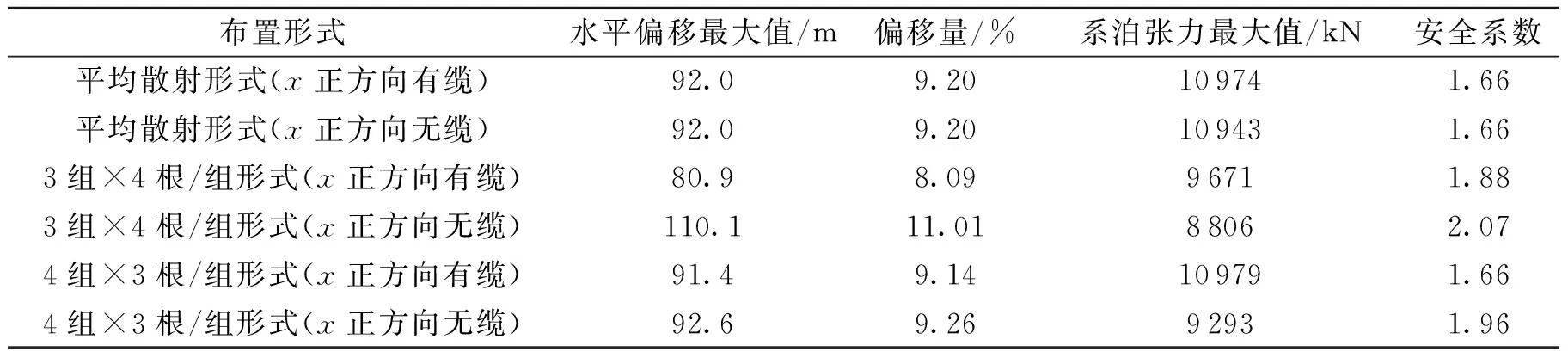
布置形式水平偏移最大值/m偏移量/%系泊张力最大值/kN安全系数 平均散射形式(x正方向有缆)92.09.20109741.66 平均散射形式(x正方向无缆)92.09.20109431.66 3组×4根/组形式(x正方向有缆)80.98.0996711.88 3组×4根/组形式(x正方向无缆)110.111.0188062.07 4组×3根/组形式(x正方向有缆)91.49.14109791.66 4组×3根/组形式(x正方向无缆)92.69.2692931.96

注:表中水平偏移指FPSO上系泊点在水平面上的总位移,是纵向位移与横向位移的矢量和.

不难看出,组式系泊模式下的安全系数比平均散射系泊模式下的高,说明组式系泊系统参与发挥系泊作用的缆较多,使组式系泊的安全系数在出现少数系泊缆断裂时更有优势.

尽管系泊缆均匀布设容易调整各系泊缆间的预张力,安装上实行一对一对布设,可使用较少的施工机具,但其缺点是发挥系泊作用的系泊缆根数少,这种布设方式适合环境条件要求低的作业工况.组式系泊模式下的FPSO水平偏移量没有明显的优势,这要取决于海况条件及FPSO的风标位置,文中所计算的工况中,3组×4根/组(x正方向有缆)系泊形式时的FPSO水平偏移量最小,且系泊安全系数较高.同样是3组×4根/组的系泊形式,当x正方向无缆时,虽然系泊安全系数最高,但FPSO的水平偏移量也偏大,超出了规范要求.以上计算的6种系泊缆布置形式中系泊安全系数均符合要求,水平偏移量除3组×4根/组形式(x正方向无缆)外均符合规范要求.

2.4.2 组式系泊缆间角度的影响

组式系泊缆一般沿圆周等夹角分布,每组多根缆间也等夹角分布(图10).同组缆间夹角θ的变化会影响FPSO的水平偏移及系泊缆动张力.在上文6种系泊缆布置形式工况中,选择3组×4根/组形式(x正方向有缆)的系泊结构作为计算工况,分析不同缆间夹角θ下FPSO的水平偏移及缆动张力计算统计值的变化规律.

图10 三组式系泊模式Fig.10 Grouped mooring mode(3groups)

表10和图11,12给出了组式系泊模式5种缆间夹角下的水平偏移量δ及系泊缆动张力σ的时域计算统计结果.

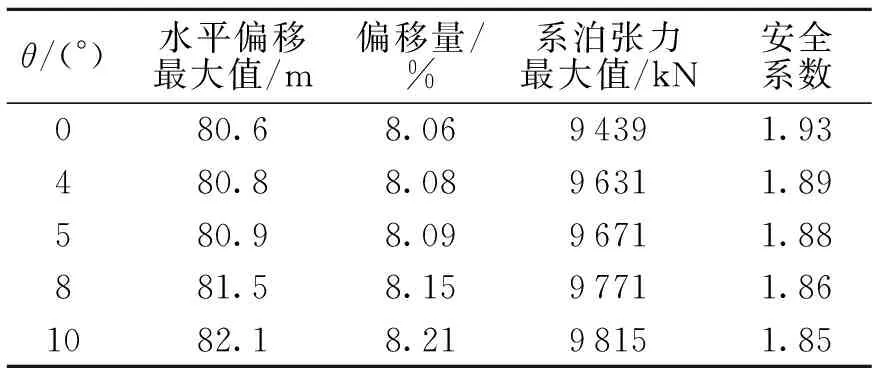
表10 不同系泊缆间夹角下FPSO水平偏移及 动张力统计值Table 10 Statistic value of the horizontal motion and mooring tension of FPSO under different angles between mooring lines

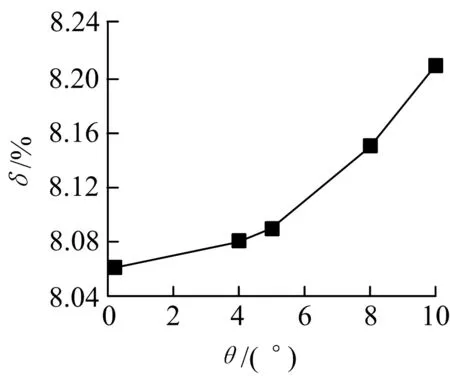
图11 不同系泊缆间夹角下FPSO水平偏移量Fig.11 Horizontal motion of FPSO under different angles between mooring lines

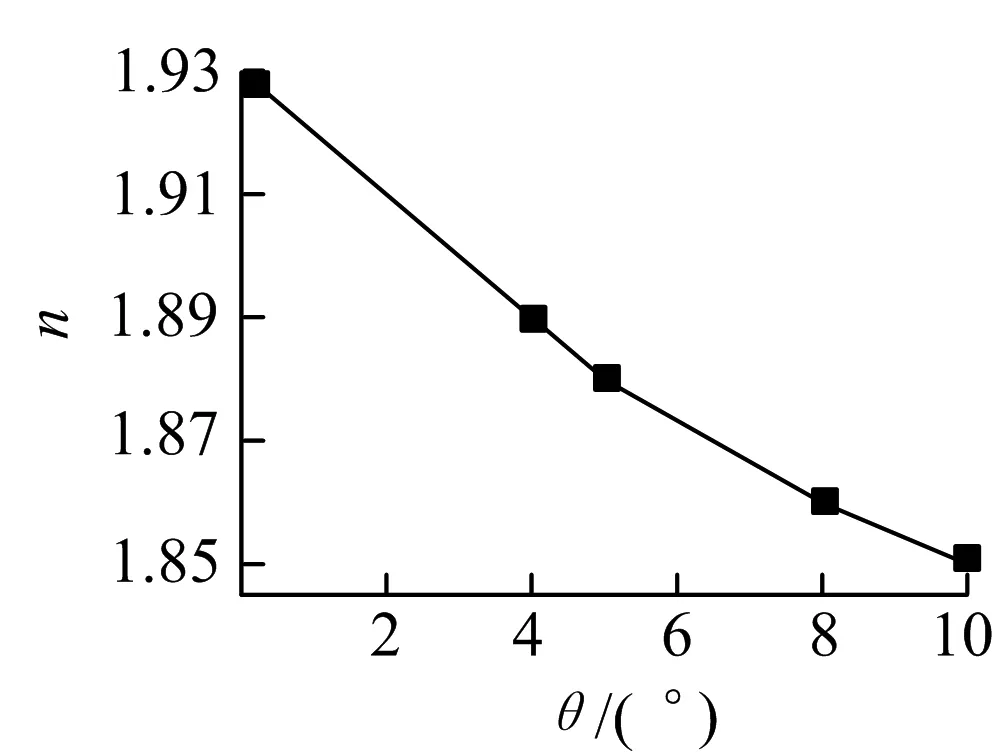
图12 不同系泊缆间夹角下系泊缆安全系数Fig.12 Safety factor of mooring lines under different angles between mooring lines

从上述图表可知,随着缆绳夹角的增加系泊安全系数减小,FPSO水平偏移量增大.在表10计算的5种工况中,FPSO偏移量与缆安全系数均符合规范要求,缆间夹角的变化对FPSO偏移量与缆安全系数有显著影响.当同组缆间夹角为0°,也就是同组四根缆位置重合时,FPSO水平偏移量最小,系泊安全系数最高.但是同组缆间夹角过小会导致缆间摩擦碰撞,存在安全隐患,且夹角太小会给海底锚的布设带来困难,综合考虑FPSO的横摇、纵摇、垂荡运动,缆间夹角并不是越小越好.

2.5 系泊缆数量对FPSO系统动力效应的影响

根据工程经验,内转塔式单点系泊系统的系泊缆数量N至少8根,以抵抗来自东、南、西、北、东南、西南、西北、东北8个方向的环境力.在上节5种系泊缆间夹角工况中,选择5°作为本节的计算工况,分析不同系泊缆数量下FPSO的水平偏移及缆动张力统计值的变化规律.

表11和图13,14给出了组式系泊模式3种缆数量下FPSO的水平偏移及系泊缆动张力的时域计算统计结果.

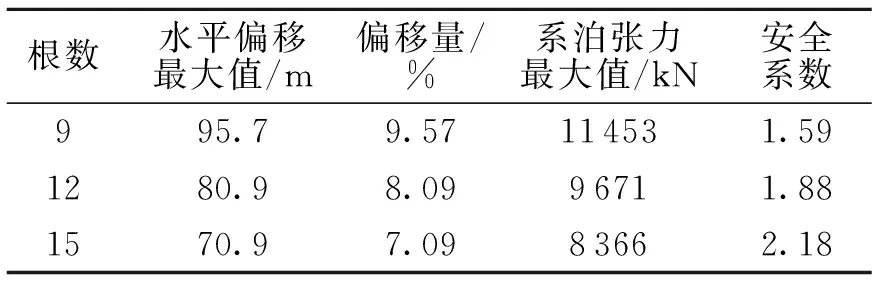
表11 不同系泊缆数量下FPSO水平偏移及 动张力统计值Table 11 Statistic value of the horizontal motion and mooring tension of FPSO under different numbers of mooring lines

图13 不同系泊缆数量下FPSO水平偏移量Fig.13 Horizontal motion of FPSO under different numbers of mooring lines

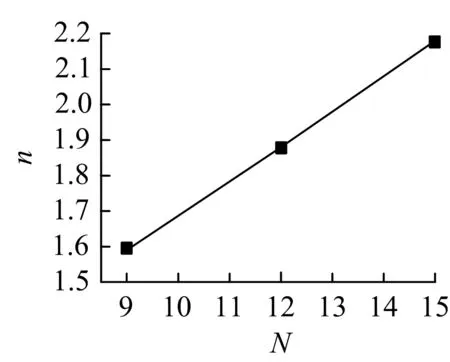
图14 不同系泊缆数量下系泊缆安全系数Fig/14 Safety factor of mooring lines under different numbers of mooring lines

不难看出,缆绳数量对单点系泊FPSO系统的动力响应有非常显著影响,随着系泊缆数量的增加,FPSO水平偏移量减小,安全系数增加,系泊性能明显变好.12根缆与15根缆的系泊系统均满足水平偏移和安全系数的规范要求,但考虑到缆数太多后会造成水下柔性软管、电缆和脐带管等布置与穿行的困难,且增加系泊缆数量将提高海上的安装工作量,增加工程投资费用.对于9根缆组式系泊的情况,FPSO水平偏移量略大,但仍在要求范围内,安全系数比规范要求的略低,但若合理修改本章中上述分析的系泊参数,9根缆也能满足系泊要求.调研得知,目前在南海7艘FPSO中系泊缆数量从8～10根不等.综合考虑各因素,9根缆组式系泊为可选方案.

2.6 系泊系统优选及其优选方案下的动力性能分析

在比较系泊参数结论的基础上,对中国南海1 000 m水深某型FPSO的单点系泊系统及其张紧式系泊缆的各项参数进行综合优选,对系泊方案进行调整,仍以中国南海百年一遇的风浪流条件作为其环境载荷,对FPSO系泊系统进行校核,以适应海上浮式结构物水平偏移量及系泊安全系数的要求.修改后的单点系泊FPSO系泊方案及主要参数如表12,13所示.

表12 FPSO单点系泊系统优选方案Table 12 Optimize proposal of single point mooring system of FPSO

表13 优选方案的缆绳参数Table 13 Main particulars of optimized mooring lines

FPSO在中国南海百年一遇的海况中,可能出现最大系泊力和最大水平偏移的环境方向组合,共7种,如表14所示[13].下面对优选调整过的系泊系统进行强度及FPSO水平偏移校核,表15中的统计值都是在FPSO达到平衡位置后,在平衡位置附近运动的时域统计值,各缆的编号如图15.

表12，13所示的FPSO系泊系统优选方案基本与工程实践经验相符.为了防止系泊线磨损和破坏,预张力一般控制在15%～30%断裂强度,文中的优选方案预张力为18.5%断裂强度;顶部预张力张角随水深的变化有所不同,一般控制在30°～50°比较合适,文中预张力倾角36°.表15列出了该系泊系统在可能出现最大系泊力和最大水平偏移的环境方向组合作用下FPSO的水平偏移量以及系泊系统的安全系数.可以看出在以上7种工况中,工况5时的系泊系统安全系数最小,工况6的水平偏移量最大.斜风作用下的水平位移比斜流作用下的位移大,安全系数比斜流作用下的安全系数小.不难看出,所有工况系泊缆张力的安全系数、FPSO的水平偏移量都满足要求.因此证明,所优选的系泊缆方案系泊性能优良,较初步设计的系泊缆方案性能有了显著地提高.

表14 计算工况Table 14 Calculation conditions

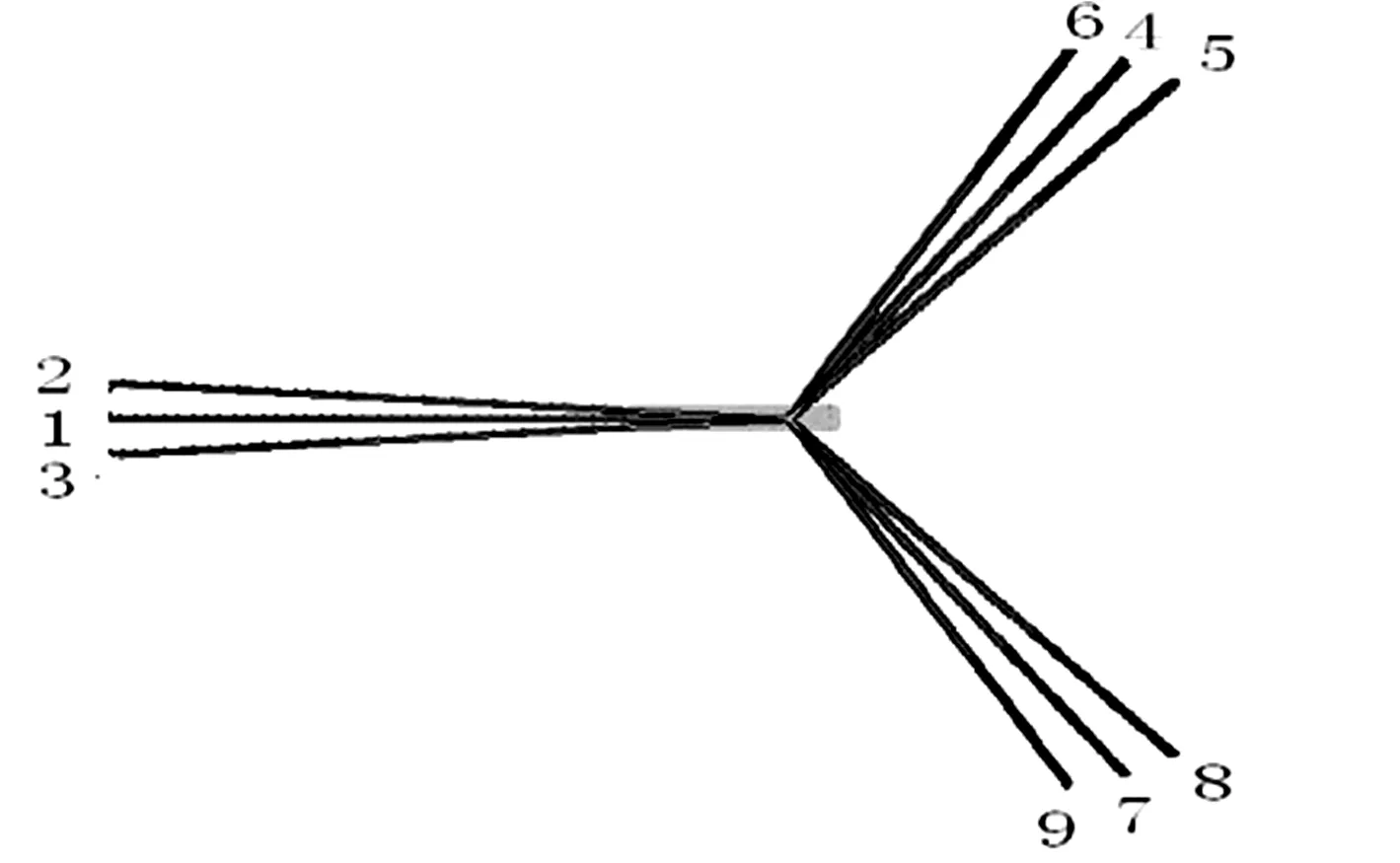
图15 FPSO系泊方案俯视图Fig.15 Planform of FPSO mooring form表15 FPSO运动响应及系泊系统张力响应Table 15 Motion response of FPSO and tension response of mooring lines

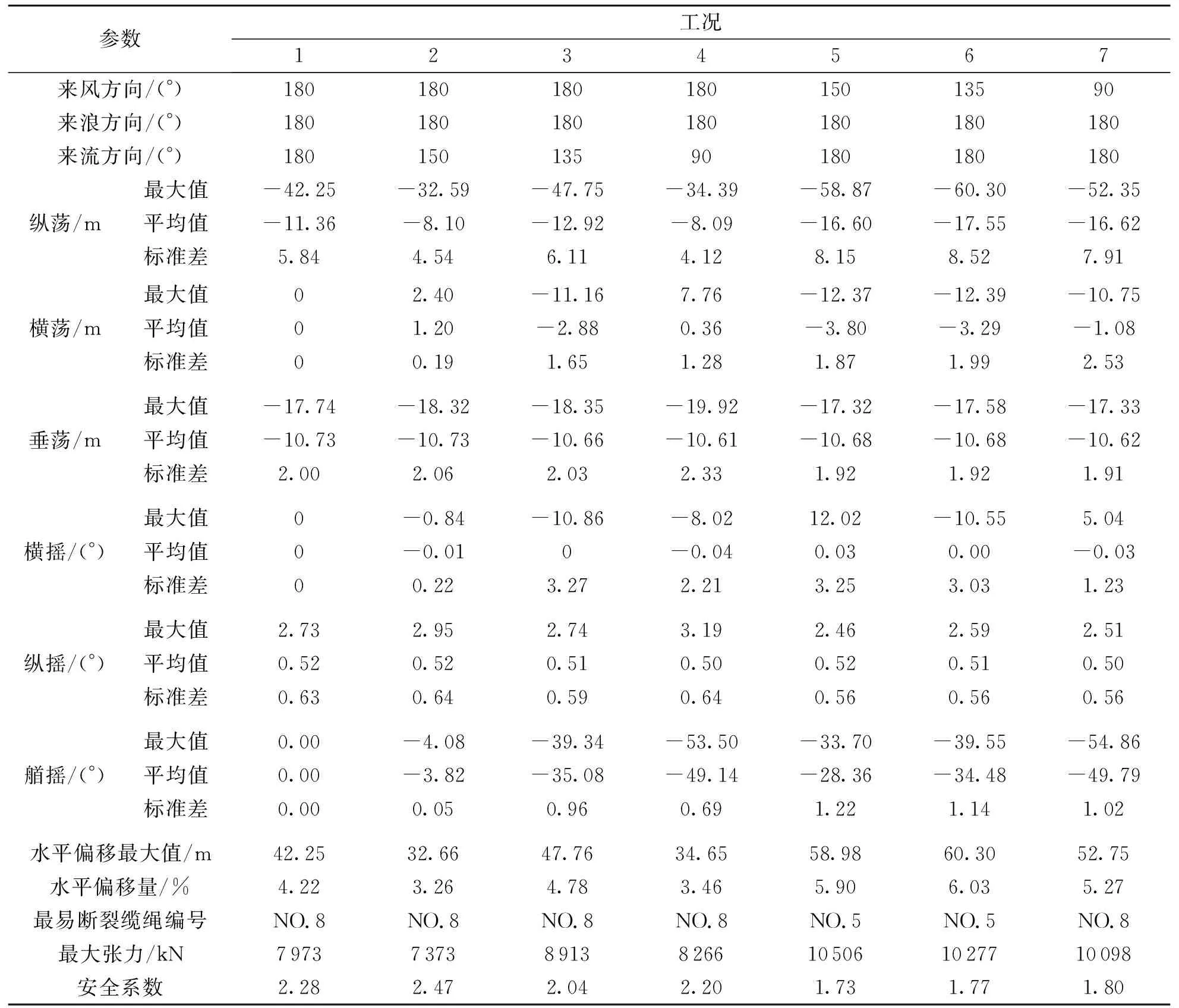
参数工况1234567来风方向/(°) 18018018018015013590 来浪方向/(°) 180180180180180180180 来流方向/(°) 18015013590180180180纵荡/m最大值-42.25-32.59-47.75-34.39-58.87-60.30-52.35平均值-11.36-8.10-12.92-8.09-16.60-17.55-16.62 标准差5.844.546.114.128.158.527.91横荡/m最大值02.40-11.167.76-12.37-12.39-10.75 平均值01.20-2.880.36-3.80-3.29-1.08 标准差00.191.651.281.871.992.53 垂荡/m 最大值-17.74-18.32-18.35-19.92-17.32-17.58-17.33 平均值-10.73-10.73-10.66-10.61-10.68-10.68-10.62 标准差2.002.062.032.331.921.921.91横摇/(°) 最大值0-0.84-10.86-8.0212.02-10.555.04 平均值0-0.010-0.040.030.00-0.03 标准差00.223.272.213.253.031.23 纵摇/(°) 最大值2.732.952.743.192.462.592.51 平均值0.520.520.510.500.520.510.50 标准差0.630.640.590.640.560.560.56艏摇/(°) 最大值0.00-4.08-39.34-53.50-33.70-39.55-54.86 平均值0.00-3.82-35.08-49.14-28.36-34.48-49.79 标准差0.000.050.960.691.221.141.02 水平偏移最大值/m42.2532.6647.7634.6558.9860.3052.75 水平偏移量/%4.223.264.783.465.906.035.27 最易断裂缆绳编号NO.8NO.8NO.8NO.8NO.5NO.5NO.8 最大张力/kN7973737389138266105061027710098 安全系数 2.282.472.042.201.731.771.80

注:表中位移的最大值为运动距离的最大值,也就是绝对值最大,因此有时为负数.

3 结论

1)文中主要探讨了内转塔位置、张紧式系泊缆材料分布、系泊缆预张力大小与方向、系泊缆数量、系泊缆布置形式等参数对FPSO系泊性能的影响,分析了不同参数时FPSO的水平偏移量及张紧式系泊缆的安全系数；

2)在综合分析系泊系统参数影响规律的基础上,提出了一套内转塔式FPSO单点系泊系统的优化方案,对所优选的系泊系统与FPSO进行了耦合运动预报,并进行了系泊缆的强度校核,结果表明：优选方案的系泊性能优良,与初步设计方案相比有了显著地提高,能够满足FPSO系泊定位的工程要求.

参考文献(References)

[ 1 ] 季春群. 各种参数对单点系泊运动及载荷的影响[J]. 中国海洋平台,2000,15(1):19-23.

Ji Chunqun. Influence of various parameters on single point mooring motion and load[J].Chinaoffshoreplatform,2000, 15(1):19-23.(in Chinese)

[ 2 ] 安维杰. 海洋石油工程设计指南[M]. 北京:石油工业出版社, 2007.

[ 3 ] Chai Chenghuang.Mooring line fatigue:a risk analysis for an SPM cage system [J].AquaculturalEngineering,2010(42):8-16.

[ 4 ] Han J S. A comparative study on the fatigue life of mooring systems with different composition [C]∥The9thInternationalConferenceonHydrodynamics.Shanghai[s.n.],2010.

[ 5 ] 周素莲, 聂武, 白勇. 深水半潜式平台系泊系统设计研究[J]. 船舶力学,2010,14(5):495-502.

Zhou Sulian, Nie Wu, Bai Yong. Investigation on mooring system design of a deepwater semi-submersible platform [J].JournalofShipMechanics,2010,14(5):495-502. (in Chinese)

[ 6 ] Arcandra. Hull/Mooring/Riser coupled dynamic analysis of a deepwater floating platform with polyester lines [D].Texas USA:Texas A&M University,2001.

[ 7 ] 刘海笑,黄泽伟. 新型深海系泊系统及数值分析技术[J]. 海洋技术,2007,26(2):6-10.

Liu Haixiao,Huang Zewei.A new deep-water mooring system and numerical analytical techniques [J].JournalofOceanTechnology,2007,26(2):6-10. (in Chinese)

[ 8 ] American Petroleum Institute.API RP 2SM,Recommended practice for design,manufacture,installation, and maintenance of synthetic fiber ropes for offshore mooring[S].Washington：API Press，2001.

[ 9 ] American Petroleum Institute.API RP 2SK,Recommended practice for design and analysis of station keeping systems for floating structures[S].Washington API Press:1997.

[10] 王世圣,谢彬,李新仲. 在南海环境条件下深水典型TLP的运动响应分析[J]. 中国造船,2011,52(1):94-101.

Wang Shisheng,Xie Bin,Li Xinzhong.The motion response analysis of deep water typical TLP in environment conditions of South China Sea [J].JournalofShipbuildingofChina,2011,52(1):94-101. (in Chinese)

[11] 李俊,杨建民,肖龙飞. 转塔位置对FPSO水动力性能的影响[J].海洋工程,2005,23(4):9-14.

Li Jun,Yang Jianmin,Xiao Longfei. Effect of turret location on the hydrodynamic performance of turret moored FPSO [J].JournaloftheOceanEngineering,2005,23(4):9-14. (in Chinese)

[12] 黎春,周齐家,冯柯来,等. FPSO系泊和定位方法[J]. 内蒙古石油化工,2010(2):45-47.

Li Chun, Zhou Qijia, Feng Kelai et al. The mooring and dynamic positioning system for FPSO[J].JournalofInnerMonguliaPetrochemicalIndustry,2010(2):45-47. (in Chinese)

[13] 杨利敏. 单点系泊船舶在风浪流联合作用下的平衡位置和受力计算[J]. 中国水运,2007,7(4):9-11.

Yang Limin. The balance position and force calculation of a single point mooring ship under the combined action of wind,wave and tide [J].JournalofChinaWaterTransport,2007,7(4):9-11. (in Chinese)