履带式起重机下车有限元分析方法研究

马 剑

(江苏科技大学 张家港校区 船舶与建筑工程学院,江苏 苏州 215600)

随着计算机技术的不断进步,大型有限元应用软件也得以不断发展,在各种工程领域广泛应用.在早期的工程机械领域中,结构计算主要是通过理论公式校核结构的刚度和强度,而多数理论公式只能将整机或部件简化为材料力学中的典型结构计算总体的刚度和强度,无法准确反映出局部细节受力和变形行为.有限元方法正好将这两方面的特点很好地结合,它所得到的数值结果有助于设计者对所设计的结构在强度和刚度方面更准确地把握.有限元方法作为一种高级而复杂的数值方法对于外部输入条件十分敏感,只有模型的单元类型、尺寸和几何形状适合,边界条件符合实际工况,才能得到较精确的数值结果.

1 履带式起重机下车有限元分析中存在的问题

履带式起重机下车包括履带梁和车架两个主要部件,作为整车的基础,不但对结构强度有严格的要求,对刚度同样也有严格要求.所以应力结果和位移结果都要关注.

在有些分析计算中[1],将履带梁和车架分开独立分析,这样虽然可以减少单个有限元模型的单元数量，节省计算时间,却也使得边界条件的确定变得困难.如果无法确定准确的受力和约束等边界条件,那就无法得到可靠的计算结果.

例如,在实际工作中履带板与地面接触面积是根据整机重心的变化而不断变化的,同时地面也是一个弹性体;履带梁与车架之间是有多种方式连接的,销轴连接或者插入式连接,不同的连接方式对应不同的载荷传递模式.如何模拟履带板与地面之间的接触行为,如何将地面作为弹性体模拟都是复杂的问题.同样，对于车架而言也需要确定与履带梁之间的连接形式,准确分析其受力后的变形模式,才能在有限元模型中进行模拟.车架与转台之间通过回转轴承连接传递载荷,如何在有限元模型中模拟回转轴承的力学特性和传递分配载荷的方式同样复杂而重要.

2 建立有限元模型

有限元基本方程[2]为

Ka=P

(1)

式中:K为单元刚度矩阵;a为节点位移矩阵;P为单元等效节点载荷矩阵.

单元刚度矩阵K的一般表达式为

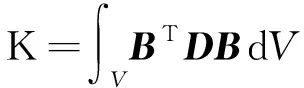
(2)

式中：B为应变矩阵；D为材料弹性矩阵；V为单元体积.

对于求解积分的收敛性和精确程度,都与积分点的选择有直接关系.根据几何关系和本构关系,通过节点位移矩阵a可以得到节点应变ε=LNa,其中N为单元插值函数矩阵.由此可见节点应变ε与插值函数N有关系.通过上述分析可以看出，积分点和插值点直接影响了求解的精确程度.在实际的有限元建模过程中,单元的排列方式直接决定了积分点和插值点,可见单元类型的选取和排列方式是影响有限元结果的一个重要因素.

对于单元等效载荷矩阵P=Pf+PT+Pδ+Pε0,它包含了作用于单元的体力f、边界分部力T、单元内力δ、初应变ε0.这就是通常有限元建模时施加的边界条件,包括重力,外载荷和刚体运动的约束.在有限元基本方程中求解的就是节点位移矩阵a,所以边界条件的重要性不言而喻.

2.1 单元的选取

履带式起重机的下车主要为板的焊接结构,根据板的力学特性在有限元模型中采用板单元模拟,以实际板的中面位置作为有限元模型中板单元的位置.对于特殊的细节结构,根据不同的力学特性采用相应的单元模拟,例如梁单元、实体单元等等.单元作为有限元模型的基础,它的形状和排列方式直接影响着数值结果的准确与否;它的数量影响着求解时间.对于板单元正方形最适宜[3],如果采用矩形单元,长宽比不宜过大.在应力变化剧烈的局部,适当增加的单元密度有利于保证计算结果的精确性(图1).

图1 应力变化剧烈处的单元排列Fig.1 Arangment of the elements where stresses change dramaticly in value

理论上单元数量越多意味着数值结果越精确.但是一味增加单元数量会使有限元模型变大,使得对模型的操作变得困难.很好地将单元数量、形状和排列方式进行配合,可以在较少单元数量的情况下获得较准确的结果.单元数量与模型的几何尺寸和求解类型有关的.

为了得到准确的应力和位移结果,而将履带梁和车架组合在一起进行分析计算.同时也使简化边界条件的确定更简单(图2).

图2 下车整体模型Fig.2 Model of the lower structure

文中的履带与车架为销轴和推力面的联接方式(图3).销孔与轴之间以接触方式传递力.推力面之间也是一种接触行为,只传递垂直于接触面方向的力,从而限制了履带梁和车架绕销轴的相对转动.这两个区域为典型的接触行为,如果采用有限元方法里的接触计算虽然可以准确模拟其受力和变形模式，同时由于接触计算是一种复杂的非线性运算,单元数量越多，所需计算时间越多,也不利于方程求解时收敛，所以这里采用了间隙单元,这是一种类似于弹簧的单元,通过对单元的控制,使其只受压,在求解过程中如果单元受拉,程序自动让其退出，不参与计算.经过反复迭代运算得到一组位置合理的受压间隙单元.这种迭代与非线性接触计算比较是一种相对简单,数值稳定性较高的非线

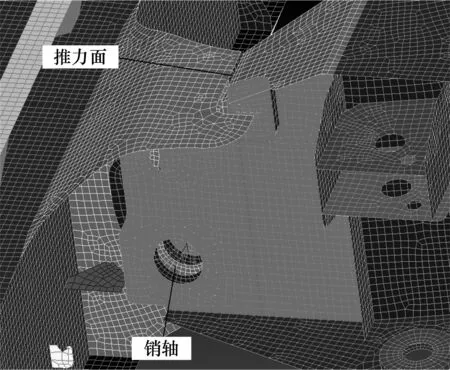
图3 履带梁与车架的联接Fig.3 Connection between the track beam and the frame性算法.在模型处理上较简单,求解时间也短.这种处理方法是用一组点接触代替面接触,会造成接触面上的应力失真,但是确保了变形模式和载荷传递的相对准确.通过提取受压间隙单元的拉力可以得到接触面上的接触力,再利用传统公式对轴和孔的强度以及接触面的接触应力进行校核.

对于双层板的焊接结构,采用一层单元模拟双层板.将单元厚度定义为双层的总厚度.将其单元的中面平移到双层板的公共中面,以保证模型的力学特性与实际结构相似.

2.2 边界条件的确定

边界条件的准确与否直接影响计算结果的可靠性.对于履带式起重机下车的有限元模型而言就是履带板与地面之间接触行为的约束模拟和回转支撑承受车架上分布载荷.载荷和约束的施加如图4.回转支撑上部所有部件和吊载的重量均被考虑,相对于回转中心(放射状梁单元的中心)计算出等效力和力矩.并施加于回转中心.履带梁的约束主要是地面的支撑力,需要在每个模拟地面支撑的间隙单元处施加垂直地面方向的约束,同时需要额外在履带梁前端施加其他两个方向的约束来控制刚体自由度,以保证有限元模型顺利求解.在所考虑的3个工况中,唯一不同的就是转弯工况.同时需要在单侧履带梁上施加转弯力,另一侧履带梁需要被完全固定.

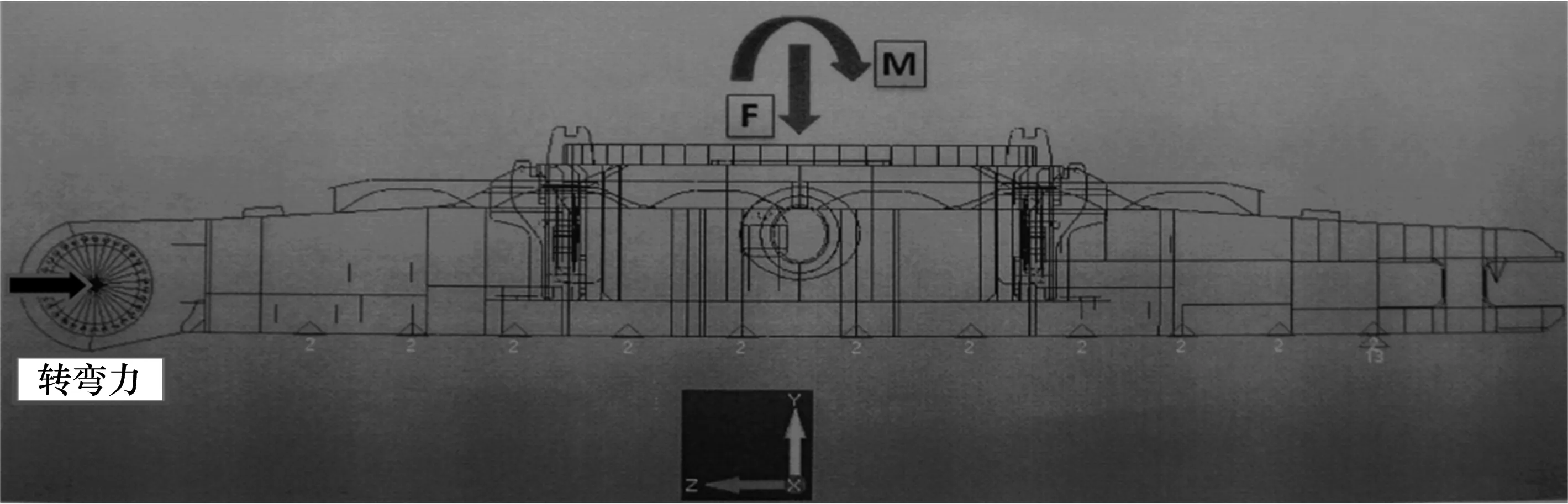
图4 边界条件Fig.4 Boundary condition

有些有限元计算中将地面直接作刚性处理,在支重轮位置施加刚性约束限制整体位移.实际上地面是作为弹性体存在的,在履带板的压力作用下产生变形.这会对履带梁受力的分布产生影响,从而影响应力值.传统的计算最大接地压力公式也是将地面和结构作刚体处理,不能很精确地反映出轮压的分布.文中将地面作为弹性体处理,同样用受压间隙单元模拟.在吊载过程中，整机重心在倾翻力矩的作用下多数情况不与回转中心重合,这时并不是所有的履带板都与地面接触,只有压在与地面接触的履带板上的支重轮受压.采用受压间隙单元模拟这一连串的接触行为,程序可以自己根据重心位置判断哪些支重轮受压而得到合理的支重轮压力分布,从而对于支重轮的布置有一定的指导意义(图5).

图5 地面约束Fig.5 Ground constraint

影响支重轮压力分布的因素除了整机重心位置外,支重轮周围履带梁结构和地面的变形情况也是重要因素,因为它们是相互作用的弹性体.局部载荷的分布也是与它们的刚度有关的.地面的刚度，即地面的软硬程度，对支重轮附近的履带梁结构的应力分布是有显著影响的.

车架所受的载荷可以简化为作用在回转中心的垂直力和倾翻力矩.倾翻力矩的大小是衡量履带式起重机起重性能的一个重要指标,也是影响整车应力和变形的最主要因素.载荷施加方式的正确与否对于结果的准确性有很大的影响.车架与转台间主要是通过回转支撑和固定用的高强螺栓载荷传递.在不考虑预紧力的情况下,可以根据传统公式[4]计算出这种在正压力和倾翻力矩共同作用下的螺栓力分布,再施加到车架的螺栓孔上.通常情况下根据公式[5]Nmax=FG/n+MR/(∑r12)来计算轴承受压,其中，N为轴力，n为螺栓个数，M为弯矩，y1,yi分别为最外排螺栓“1”和第i排螺栓到转动轴的距离，转动轴通常取在弯矩指向一侧最外排螺栓处，m为螺栓的纵向列数.对于紧固回转支撑的螺栓力计算也是基于此公式.这种传统公式计算所得的螺栓力完全由载荷的大小和螺栓到回转支撑安装面对称轴的距离决定.实际情况是下车结构的刚度不是均匀分布,尤其是螺栓孔周围刚度不均匀,对螺栓力的分布影响很大.

为了使载荷在车架上的分布更真实,用梁单元模拟回转支撑和固定螺栓,使局部刚度更接近实际情况.以放射状的梁单元连接回转中心和每个螺栓,将施加在中心的载荷分配到每个螺栓,这样就可以较真实地反映出结构刚度对载荷分配的影响(图6).

图6 模拟回转支撑分配载荷Fig.6 Distribution load on the rotary support

用于模拟回转支撑和螺栓的梁单元截面形状与实际相符,而放射状梁单元的截面属性随着履带式起重机的型号不同也略有不同.由于螺栓预紧力为内力,只对螺栓孔局部应力有影响,且对于每个螺栓都是相同的,所以并未在文中的有限元模型中考虑,而是通过手册[4]中的公式对螺栓和螺纹进行了校核.

3 计算工况选取

履带式起重机下车的有限元计算主要分为3类工况:① 起臂工况;② 吊载工况;③ 转弯工况.对于不同的工况,下车受力状态也不相同,所关心的结构局部也不同.

起臂工况主要是臂架重心距离回转中心较远,造成倾翻稳定性较差.臂架越长越危险,通常取最长臂起臂工况进行分析.履带梁的长度直接决定了起臂工况的倾翻稳定,为了提高倾翻稳定性能,长臂起臂时采用履带梁头部下面垫楔块的方式.正前方起臂时履带梁头部受力情况较复杂,是需要重点关注的部分.

转弯工况主要模拟当一条履带梁被固定住,另一条履带梁的驱动马达输出最大扭矩时的情况.履带梁与车架连接的局部是重点关注的对象,包括连接销轴和推力面的受力.

由于下车的结构可以近似看作是中心对称结构,加之是360°回转吊载,所以只要在0～90°之间选择回转角度进行吊载工况计算,所得结果基本就可以代表360°的各个吊载位置.一般情况下选择0°、30°、45°、60°和90° 5个比较有代表性的回转角度来计算.起重量的选择主要分为两类:① 最大起重重量;② 最大倾翻力矩或者最大起重力矩.为了使结构有足够的强度储备,在结构测试时要求起重量要达到125%超载,在有限元计算中则采用133%超载.计算的载荷范围就包括了100%，125%和133%超载.将以上的各种因素加以组合就会出现多种工况.吊载工况下履带梁与车架连接的局部以及车架的回转支撑安装面附近是需要重点关注的区域.

对于不同的吊载工况安全系数也是不同的.除了根据相关规范的要求选取安全系数.根据每种工况的危险程度、出现频率和状态持续时间来决定安全系数.在一些特殊情况下根据生产实践中积累的经验来决定适当的安全系数也是常见的情况.

4 计算结果

依据以上分析，如图7～10,4种工况下，下车的大部分区域应力很低,局部小面积有高应力出现,但是也都在设计范围之内.通过对比结构应力测试结果发现,转台和下车应力方向的单一测点,测试结果与有限元计算结果的平均偏差在8.5%左右,最大偏差为12.5%.对于应力方向复杂的测点,由于单个应变片只能测得单一方向的应力,而应变花中的各个应变片所测得的应力并不是严格意义上的同一点,所以测试结果与计算结果偏差较大,但测试结果也在设计范围内.通过结果对比(图11)可以看出边界条件基本准确.

图7 最长臂起臂工况应力云图Fig.7 Stress contour under the arm operation condition

图8 最大倾翻力矩133%超载正前吊载应力云图Fig.8 Stress contour of the front suspension case with 133% overload

图9 最大倾翻力矩133%超载回转30度吊载应力云图Fig.9 Stress contour of the 30° suspension case with 133% overload

图10 转弯工况应力云图Fig.10 Stress contour under the turn condition

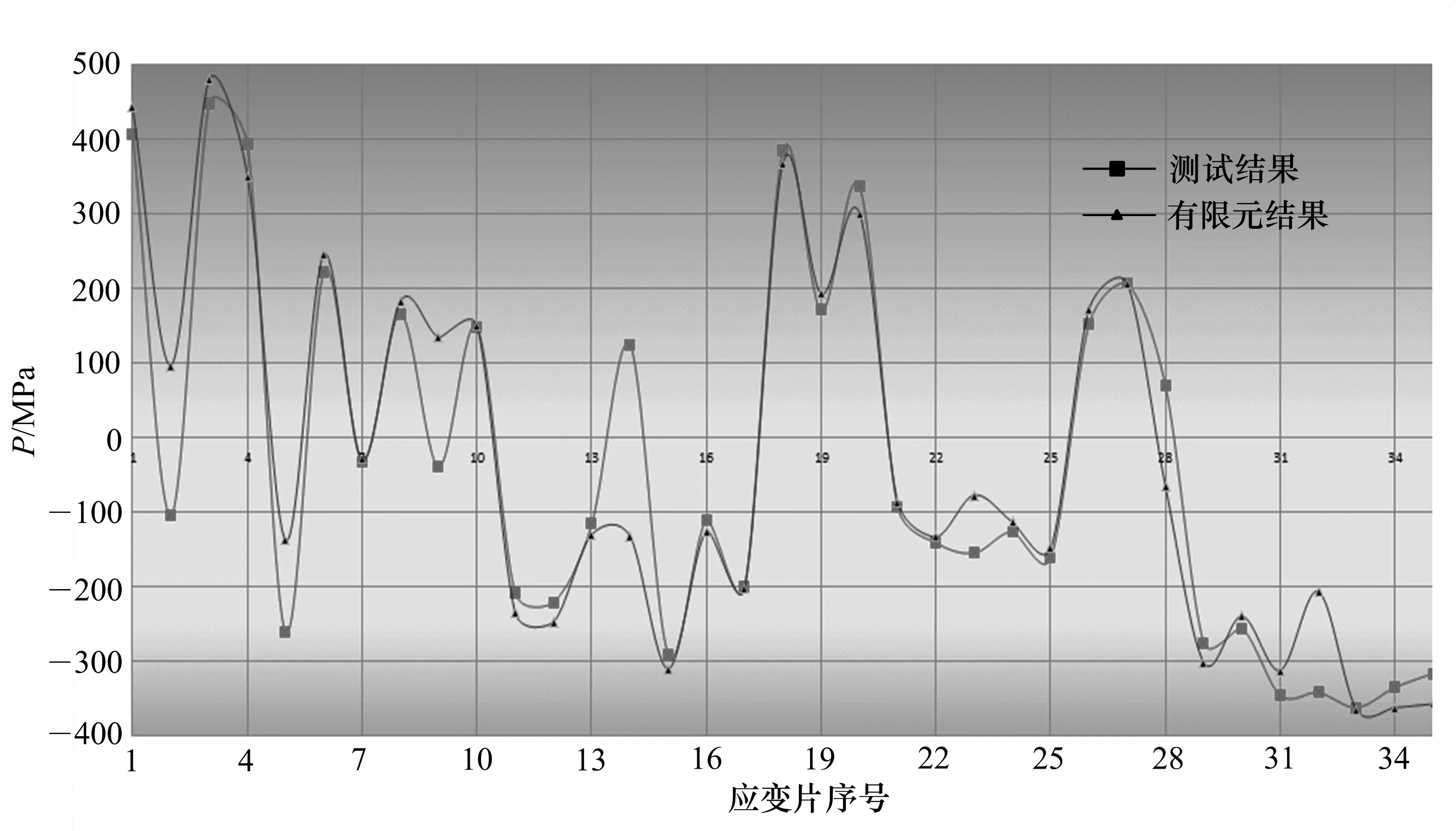
图11 测试结果与有限元结果对比曲线Fig.11 Result comparison curve

有限元分析在得到应力云图的同时也得到了位移云图.通过分析位移云图是否合理也可以判断边界条件的准确性,这里就不一一列举.

5 结论

有限元方法能够较准确地模拟工程机械局部的受力和变形行为,但前提是采用合适的单元,更重要的是边界条件符合实际工况.国内学者将履带梁和车架分开独立分析,使得边界条件的确定变得困难,难以得到可靠的计算结果.

文中将履带式起重机下车包括履带梁和车架两个主要部件,作为整车使用有限元分析,通过将单元数量、形状和排列方式进行配合,可以在使用较少单元数量的情况下获得较准确的结果.为准确施加边界条件,用间隙单元模拟地面和履带的接触;用梁单元模拟回转支撑和固定螺栓,使局部刚度更接近实际情况,并使载荷在车架上的分布更真实.

计算时考虑3种工况:起臂、吊载和转弯工况.应力计算结果与实测值对比结果大致吻合(图11),论证了方法的可行性，而且从第4部分的应力云图分析可以发现,结构总体的应力偏低,具有很大的强度余量.制约这些强度余量被释放的一个因素就是局部小面积的高应力.如果结构刚度变化设计更合理,将会降低这种局部高应力,释放多余的强度储备.这只是从静力学结构强度的角度出发所得的结论.在设计过程中还有很多因素决定结构具体形式,例如刚度、稳定性和动力学特性等等.尤其是稳定性和动力学特性的分析是比静力学复杂得多的力学问题,随着工程实践经验的积累和对各种测试结果的对比分析,有待于进一步研究.

参考文献(References)

[1] 成凯,王锌,赵二飞，等.履带起重机履带架的非线性有限元分析[J].中国工程机械学报,2009,7(1):68-72.

Cheng Kai,Wang Xin,Zhao Erfei.Nonlinear finite element analysis on caterpillar frame of crawler cranes[J].ChineseJournalofConstructionMachinery,2009,7(1):68-72.(in Chinese)

[2] 王勖成.有限单元法[M].北京:清华大学出版社,2003:190-191.

[3] 朱永梅,李成涛.基于随机有限元的空间梁板结构系统可靠性分析[J].江苏科技大学学报：自然科学版,2010,24(6)：563-567.

Zhu Yongmei,Li Chengtao.Reliability analysis for beam and shell structure based on stochastic finite element method[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2010,24(6):563-567.(in Chinese)

[4] 徐灏.机械设计手册：4卷[M].2版.北京:机械工业出版社,2000,88-89.

[5] 张质文.起重机设计手册[M].北京:中国铁道出版社,1997,53-55.