基于优化旋转矢量双子样算法的捷联惯导姿态解算
唐 炜, 刘林飞, 张 鹏, 胡海秀
(江苏科技大学 机械工程学院,江苏 镇江 212003)
在捷联惯导系统中,载体的所有导航信息都从当前姿态阵中获取.从某种意义上说,姿态阵的可靠度将直接影响着系统的导航精度,故如何选择合适的算法对姿态矩阵进行实时更新就成为了整个导航过程中最核心的工作[1-2].
传统四元数法由于计算量小、可靠性高、可在全姿态下工作等突出特点在工程实践中得到了广泛应用,但该算法本身的缺陷使得其对不可交换性误差无法作出有效补偿,而且误差累积效应也比较明显.等效旋转矢量法则可以有效降低这一误差的影响,文献[3-4]推导了等效旋转矢量双子样算法微分方程的增强型解,但并未进行优化,实际上在采样时间间隔内角速度不可能完全理想化,因此算法本身尚待完善.对于捷联惯导姿态算法来说,圆锥运动是最恶劣的工作环境条件,它可以引起姿态解算的严重漂移.故确保圆锥运动环境条件下的算法漂移最小,就一定能确保在其余环境条件下的算法漂移最小[5].此外,随着算法的子样数增多和采样频率的提高,姿态矩阵计算会更加准确,但也将造成导航计算机的运算工作量快速增加,从而对系统的实时性造成不利影响.故如何寻求一种能有效兼顾系统实时性与导航精度的姿态解算算法就显得十分必要.
文中基于圆锥运动环境,分别应用四元数法和优化旋转矢量双子样算法对捷联惯导系统进行姿态解算,并对它们的解算误差加以分析和比较,以期为姿态算法的工程化应用提供相应参考.
1 旋转矢量双子样算法
1.1 旋转矢量与姿态四元数
旋转矢量法的姿态阵实时更新实际上就是通过不断采集各陀螺仪与加速度计的输出,计算出变化的四元数,并与姿态四元数运算以实现对当前姿态四元数的更新.
设tk时刻的机体坐标系为b(k),导航坐标系为n(k).记b(k)至b(k+1)的旋转四元数为q(h),则姿态阵的更新方程为:
(1)
式中:Φ为b(k)至b(k+1)的等效旋转矢量,φ=‖Φ‖,q(h)也称为[tk,tk+1]时间段内的姿态四元数.
1.2 旋转矢量与微分方程
在tk≤t≤tk+1采样间隔内,根据式(1)可得如下方程:
Q(t)=Q(tk)⊗q(t-tk)
(2)
经过化简运算,即可得到等效旋转矢量的微分方程,即Bortz方程[6]:

(3)
对式(3)中的三角函数作展开,略去高次项,可得到工程实践常用方程:

(4)
从式(4)可以看出,旋转矢量的导数等于相应的角速率再加上两项,这两项修正项实际上表明了等效旋转矢量法对不可交换性误差所做出的补偿.
1.3 旋转矢量双子样算法
因采样区间不可能无限小,故在采样间隔内进行动态积分就必定会带来误差,且会随时间增加而不断累积.此外,引起误差漂移的因素还有陀螺仪常值漂移、传感器初始对准精度等.在此不涉及如何减小误差漂移,而仅考虑姿态解算方法自身的有效性.在姿态更新周期内,拟合曲线阶数越高,子样数越多,则算法精度就越高,但也会造成运算量明显增加而影响到解算的实时性.为了兼顾系统精度及其实时性,文中采用等效旋转矢量双子样算法进行姿态解算,并在此基础上推导误差补偿项,以获得更加精确的解[7-9].
设姿态更新周期为h,采用直线拟合角速度.即令角速度的模型为

(5)
并记角增量为

(6)
则可得到角速度、角增量各阶导数的以下关系:

(7)
由于姿态更新周期一般为毫秒级,Φ可视为小量,故将第2项Φ用角增量Δθ代替,得

(8)
将等效旋转矢量按照Taylor级数展开,可得

(9)
计算式(8)的各阶导数,并将结果代入式(9)继续化简,得

(10)
令Δθ1,Δθ2分别为[tk,tk+0.5h],[tk+0.5h,tk+1]时间段内的角增量,对式(6)分段积分

(11)
将式(11)代入式(10),化简整理后可得

(12)
式(12)是式(8)的精确解.与传统等效旋转矢量双子样算法相比,此处的计算结果多出一项Σ(h).在此,将Σ(h)称为等效旋转矢量双子样算法的误差补偿项.
2 圆锥运动环境下算法优化
2.1 圆锥运动模型
假设b系为载体的瞬时坐标系O-xyz,R系为载体平衡时的坐标系O-XYZ,b系的运动角速度为ω,半锥角α为小角,即b系在R系附近微幅摆动.运动轨迹如图1,这种运动称为圆锥运动.

图1 圆锥运动示意图Fig.1 Conning motion
将R系至b系的变换看作是无中间过程的一次性等效旋转,则旋转瞬轴可表示为
(13)
2.2 圆锥运动与子样
w(t)=
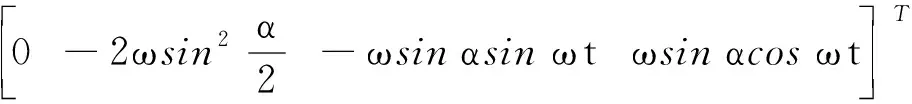
(14)
故b系相对于R系的角速度为

(15)
设Δθ1,Δθ2为姿态更新周期h二等分的角增量输出
(16)
根据式(15)可得

(17)
记

(18)
2.3 圆锥运动下的系数优化
根据式(12)可假设
Φ(h)=Δθ1+Δθ2+k1Δθ1×Δθ2+k2Δθ1×(Δθ1×Δθ2)+k3Δθ2×(Δθ1×Δθ2)
(19)
式中:k1,k2,k3均为待定优化系数,优化的标准是圆锥运动环境下算法漂移最小.由于实际在姿态更新周期内角速度变化规律不一定按直线变化,故k1,k2,k3不一定与式(12)对应项的系数相同.
将式(14)展开,并将式(18)代入化简可得

(20)

(21)

(22)


(23)
将三角函数按照Taylor级数展开并取前3项,代入化简整理后可得

(24)

(25)
将式(25)代入式(19),并与式(12)进行对比,在兼顾直线拟合和圆锥运动优化所得的两个方程的基础上来求解未知数.在此定义函数Ψ为

(26)
整理并化简可得

(27)
根据最小方差原则确定k2和k3.令k2=k3=k,引出函数f:

(28)
此时求解k2和k3就转化为求解函数f的最小值问题.当f取最小值时

(29)
故旋转矢量双子样算法在圆锥运动环境下的优化算法为:
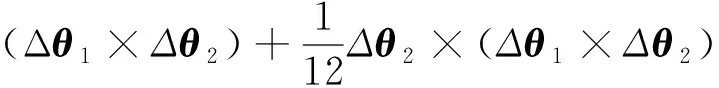
(30)
3 解算实例分析
3.1 实验条件
本实验使用了2TS-450双轴速率位置转台,它可同时设置内框(绕Z轴)和外框(绕Y轴)的运动规律,且以报文的形式对外实时输出其运动状态.在此将沿三轴相互正交配置的陀螺仪和加速度计安装于转台中心位置,使转台内、外框分别按以下两种正弦规律运动:①规律1:内、外框振幅为10°,摆动周期为1 s;②规律2:内、外框振幅为8°,摆动周期为1.25 s.两种情况下均待转台运行稳定后,开始多通道采集转台和传感器的数据,采样频率为400 Hz,时间为25 s.
3.2 解算对比分析
在此分别应用传统四元数法和优化旋转矢量双子样法两种算法进行捷联惯导姿态解算,并将两种情况下解算结果与转台标准信号进行对比分析.
1)规律1下的传感器输出航向角速率和横滚角速率原始信号见图2.系统姿态解算出的航向角误差和横滚角误差分别如图3,4.惯导解算误差累积效应不可避免,故姿态角会存在误差漂移现象.
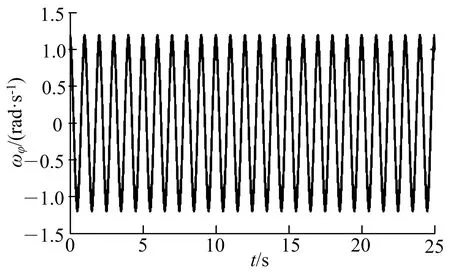
a)航向角速率

b) 横滚角速率图2 规律1下的陀螺仪输出角速率原始信号Fig.2 Original curves of ωφ-t & ωγ-t under swing pattern 1

a)四元数法

b) 优化旋转矢量双子样算法图3 规律1下解算后的航向角误差Fig.3 Curves of φ error under swing pattern 1

a)四元数法

b) 优化旋转矢量双子样算法图4 规律1下解算后的横滚角误差Fig.4 Curves of γ error under swing pattern 1
2)规律2下的传感器输出航向角速率和横滚角速率原始信号见图5.系统姿态解算出的航向角误差和横滚角误差分别如图6,7.

a) 航向角速率

b) 横滚角速率图5 规律2下的陀螺仪输出角速率原始信号Fig.5 Original curves of ωφ-t & ωγ-t under swing pattern 2

a) 四元数法

b) 优化旋转矢量双子样算法图6 规律2下解算后的航向角误差Fig.6 Curves of φ error under swing pattern 2

a) 四元数法

b)优化旋转矢量双子样算法图7 规律2下解算后的横滚角误差Fig.7 Curves of γ error under swing pattern 2表1 姿态解算误差的方差对比Table 1 Variances of attitude errors about two algorithms

算法摆动规律1航向角误差方差横滚角误差方差摆动规律2 航向角误差方差横滚角误差方差 四元数法1.311E-0021.377E-0025.126E-0035.257E-003 优化旋转矢量双子样算法4.187E-0033.925E-0031.753E-0031.484E-003
表1为转台在上述两种摆动规律条件下,两种算法解算误差在剔除一次趋势项后的方差对比.
通过对比分析,可得到如下结论:① 从理论上分析,由于采样时间不能趋近无穷小以及截断性误差等影响因素的存在,两种算法都会有不同程度的误差存在,但是相同情况下,优化旋转矢量双子样算法的误差值相对较小;② 由于增加了优化后的误差补偿项,加之旋转矢量法自身特点,故优化旋转矢量双子样算法的解算结果会比四元数法更加精确;③ 由于实验是采用双轴输入,故解算结果会存在一定的相互影响,但即便如此,旋转矢量双子样算法对误差累积的抑制效果依然比四元数法要好;④ 与四元数法相比,旋转矢量双子样算法的计算时间会有所增加,但并没有影响系统解算的实时性.
4 结论
文中分别利用四元数法和优化旋转矢量双子样算法对捷联惯导系统进行姿态解算.通过对比可知,在相同工作环境下,优化旋转矢量双子样算法的计算量虽有所增加,但在满足系统实时性要求的前提下可较明显地提高姿态解算精度.此外,优化旋转矢量双子样算法本身还能有效降低不可交换性误差以及误差累积效应对系统精度的不良影响,可有效弥补四元数法在这一方面存在的不足.实例表明,优化旋转矢量双子样算法在低子样数的情况下对如何有效提高系统精度具有重要的参考价值.
参考文献(References)
[ 1 ] 张树侠.捷联式惯性导航系统原理[M].哈尔滨:哈尔滨工程大学出版社,1992:11-20.
[ 2 ] Bortz J E.A new mathematical formulation for strapdown inertial navigation[J].IEEETransactionsonAerospaceandElectronicSystems,1971,7(1):61-66.
[ 3 ] 屈熠,赵忠. 增强型等效旋转矢量算法在圆锥运动下的仿真[J].计算机仿真,2010,11(3):25-27.
Qu Yi,Zhao Zhong. Simulation of improved rotation vector algorithm in coning motion[J].ComputerSimulation,2010,11(3):25-27.(in Chinese)
[ 4 ] 李海涛,曹咏弘,祖静. 等效旋转矢量法在旋转弹姿态解算中的应用[J].测试技术学报,2011,25(4):287-291.
Li Haitao,Cao Yonghong,Zu Jing. Application of rotation vector algorithm to attitude updating for spinning projectiles[J].JournalofTestandMeasurementTechnology,2011,25(4):287-291.(in Chinese)
[ 5 ] 马捷,孟超,王玮,等. 三子样旋转矢量优化姿态算法在捷联惯导中的研究[J].火炮发射与控制学报,2009 (3): 25-28.
Ma Jie,Meng Chao,Wang Wei,et al. Research on optimal attitude algorithm of 3-subsample rotation vector in strapdown inertial navigation system[J].JournalofGunLaunch&Control,2009(3): 25-28.(in Chinese)
[ 6 ] 张军,王直,刘维亭. SINS/Two-antenna GPS组合导航系统设计及实现方案[J]. 江苏科技大学学报:自然科学版,2004,18 (5): 43-46.
Zhang Jun,Wang Zhi,Liu Weiting. Design and realization of SINS/Two-antenna GPS integrated navigation system[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2004,18 (5):43-46.(in Chinese)
[ 7 ] 张泽,段广仁. 捷联惯导四子样旋转矢量姿态更新算法[J].控制工程,2010,17(3):272-274.
Zhang Ze, Duan Guangren. On four-sample rotation vector algorithm for SINS attitude updating[J].ControlEngineeringofChina,2010, 17(3):272-274.(in Chinese)
[ 8 ] 秦永元,张士邈.捷联惯导姿态更新的四子样旋转矢量优化算法研究[J].中国惯性技术学报,2001, 9(4):1-3.
Qin Yongyuan, Zhang Shimiao. Research on optimal four-sample rotation vector algorithm for SINS attitude updating[J].JournalofChineseInertialTechnology, 2001,9(4):1-3.(in Chinese)
[ 9 ] 祝燕华,刘建业,曾庆化,等. 等效旋转矢量系数优化的参数解析法[J]. 中国惯性技术学报,2008,16(1): 46-62.
Zhu Yanhua,Liu Jianye,Zeng Qinghua,et al.Parameter analysis method for optimizing rotation vector[J].JournalofChineseInertialTechnology,2008,16(1).46-62(in Chinese)
[10] 秦永元.惯性导航[M].北京:科学出版社,2006:320-325.

