降雨要素对土质边坡稳定性的影响分析

梅 岭, 纵 岗, 姜朋明, 陈小健

(江苏科技大学 土木工程与建筑学院,江苏 镇江 212003)

降雨作为一种常见的天气现象,是诱发土体滑坡的重要因素之一.因降雨而导致土体内部的孔隙水压力发生变化,基质吸力减小,土体的抗剪强度降低,从而引发山体滑坡、泥石流等自然灾害的发生.不同的降雨强度和降雨历时对边坡稳定性的影响程度也不同.因此研究各种雨况下的边坡稳定性十分必要.西南地区作为我国滑坡事故的多发地带,针对该地区的降雨特点,就短时强降雨和长时弱降雨对边坡的危害程度进行对比研究,为土体滑坡的预防和治理提供理论参考.

1 饱和-非饱和渗流理论

在降雨条件下的边坡渗流场的分析中,雨水的流动是典型的二维饱和非饱和问题,达西定律仍然适用其渗流规律的描述.土体内非饱和饱和渗流的控制方程[1-4]形式为:

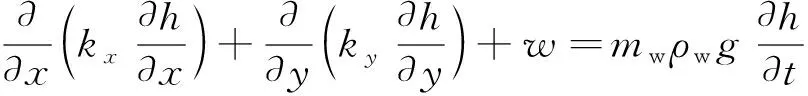
(1)

式中:h为总水头;kx和ky为x和y方向的渗透系数;w为汇源项;mw为比水容量;ρw为水的密度;g为重力加速度;t为时间.

边界条件为:

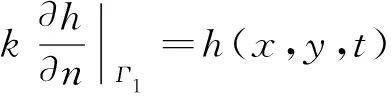
(2)

(3)

初始条件为:h(x,y,0)=h0(x,y)∈Ω

(4)

所使用的土水特征曲线模型为V-G[5]数学模型:

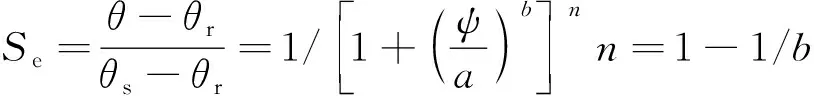
(5)

式中:a,b,n为拟合参数;ψ为基质吸力;θ为体积含水量;θs为饱和体积含水量;θr为残余体积含水量;Se为饱和度.

降雨过程的土-水特征曲线为吸湿过程值,本模型中的土水特征曲线如图1.

图1 吸湿过程的土-水特征曲线Fig.1 SWCC of absorption

2 非饱和土的抗剪强度理论

非饱和土的抗剪强度随着土体含水量的变化而变化.比较有代表性的非饱和土抗剪强度理论为毕肖普(Bishop)理论和弗雷德朗德(Fredlund)理论[6-8].

1960年毕肖普等人提出了非饱和土的抗剪强度公式:

τf=c′+[(σ-ua)+x(ua-uw)]tanφ′

式中:τf为非饱和土的抗剪强度;c′为有效粘聚力;φ′为有效内摩擦角;σ为总应力;ua为孔隙气压力;uw为孔隙水压力;x为与饱和度有关的参数;(ua-uw)为基质吸力.

基质吸力的方向和有效应力的方向不一致,在计算摩擦力时不能简单地叠加.1978年,弗雷德朗德以正应力与基质吸力作为变量对非饱和土的抗剪强度公式进行了修改.

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

式中:c′为有效粘聚力;φ′为与净法向应力分量(σ-ua)有关的内摩擦角;φb为与基质吸力(ua-uw)有关的内摩擦角;σ为破坏面上的法向总应力;ua为破坏面上的孔隙气压力.

3 建立模型和确定计算方案

以某一均质边坡作为研究对象,该边坡土体饱和时的渗透系数为0.018 m/h,弹性模量和泊松比分别为E=10 MPa，V=0.3,初始孔隙比为e=1,凝聚力c′=15 kPa,摩擦角φ′=30°，坡角为40°,初始地下水位位于坡脚处,边坡尺寸如图2.采用ABAQUS有限元分析软件对其进行模拟,计算网格如图3.

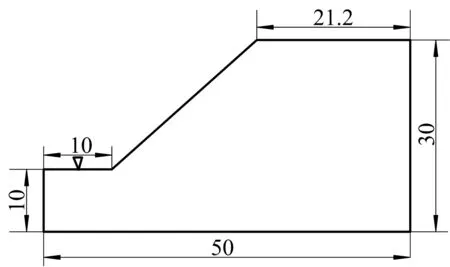
图2 边坡尺寸(单位:m)Fig.2 Slope size (unit:m)

图3 计算网格模型Fig.3 Computing grid model

为了分析降雨强度、降雨历时、短时强降雨及长时弱降雨对边坡稳定性的影响规律,采用表1～表3的计算方案.

表1 考虑降雨强度变化影响的计算方案Table 1 Calculation scheme of considering influence of rainfall intensity change

表2 考虑降雨历时变化影响的计算方案Table 2 Calculation scheme of considering influence of rainfall duration change

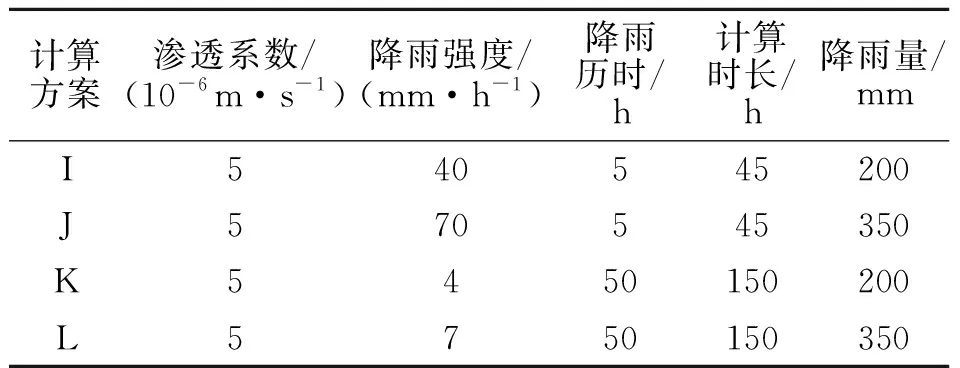
表3 短时强降雨、长时弱降雨对比方案Table 3 Short-term strong rainfall,long weak rainfall contrast scheme

4 计算结果分析

图4为上述边坡在经历了不同的降雨强度情况下,降雨结束时坡肩的孔隙水压力随着深度的变化规律.从图中可以看出,随着降雨强度的增加,边坡内的孔隙水压力在降雨后逐渐升高,在坡顶位置处升高幅度最大.降雨对边坡的影响深度大约在15 m,这就说明对于此类边坡而言,降雨虽然能够导致基质吸力变化影响土体的抗剪强度,但是在超过了一定深度的边坡内,降雨对土体抗剪强度的影响甚小基本上可以忽略.当然,边坡的渗透系数不同,降雨对其影响深度也是不同的.一般而言,土体渗透系数越大,降雨对边坡的影响深度也就越深.

图5为不同降雨强度下,边坡安全系数(Fs)的变化情况.从图中可以看出,降雨历时一定时,随着降雨强度的增加,边坡的安全系数随之减小.这是因为在降雨强度小于土体入渗强度的情况下,降雨强度越大,雨水入渗量越多,基质吸力减小导致坡体安全性降低.由于开始阶段降雨强度较小而土体的入渗能力较大,安全系数的降低幅度最大.

图6为上述边坡在经历了不同的降雨历时的情况下,降雨结束时的坡肩孔隙水压力随深度的变化规律.从图中可以看出,与降雨前相比,雨后边坡的孔隙水压力上升,在降雨影响的深度范围内,上升的幅度大致相同,约为50 kPa.随着降雨历时的增加,孔隙水压力增加较小,但是影响深度有所增加.当降雨历时为12 h时,影响深度为15 m左右;当历时为96 h时,影响深度扩大到了20 m左右.主要原因是:降雨强度不变且相对较小,雨量增加且全部渗入土体,没有在边坡上部区域形成暂态饱和区(即降雨强度较大时,雨水渗入土坡但来不及全部下渗,导致边坡非饱和区上部的含水量逐渐增大,接近饱和,形成饱和区;但降雨减小,雨水全部下渗以后,饱和区就会消失,称之为暂态饱和区),所以孔隙水压力变化较为均匀,只是入渗深度有所增加.

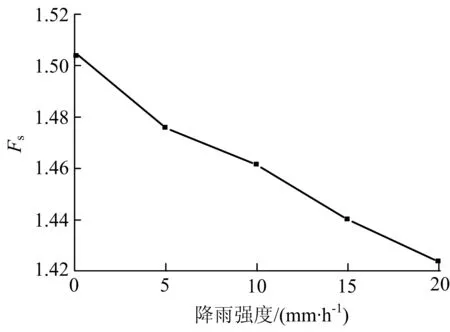
图5 安全系数随降雨强度变化Fig.5 Safety coefficient with the rainfall intensity change

图6 不同降雨历时下,孔隙水压力随高程的变化Fig.6 Under different rainfall duration, pore water pressure with elevation changes

图7为不同的降雨历时下,边坡安全系数的变化情况.从图可以看出,当降雨强度不变时,边坡的安全系数随着降雨持续时间的增加而不断减小.在开始的12 h内,边坡安全系数降低幅度最大,之后的时间内安全系数虽然也在降低,但是降低的幅度明显变缓.这是因为在降雨的初期,土体的入渗能力大,雨水基本上全部渗入,随着入渗量的增加,土体的入渗能力减小,从而使土体含水量增加的趋势减慢,安全系数降低的幅度也就变缓了.

图8为上述边坡在经历短时强降雨、长时弱降雨两种不同雨况下,边坡坡肩孔隙水压力随高程变化的对比图.在I，J短时强降雨方案下,表层的土体(5 m以内)孔隙水压力几乎增到0 kPa,接近饱和状态.主要原因是此时的降雨强度大于土体的饱和渗透系数,水分在边坡内部的运移很慢,在边坡的上部形成暂态饱和区.K,L长时弱降雨方案下,上部土体远远没有达到饱和,只是影响深度加大.也就是说如果一旦发生土体滑坡,长时弱降雨下的滑坡危害性会更大.因为短时强降雨下的滑坡多会发生在边坡的上部,滑坡土体的体积相对较小.而长时弱降雨下的滑坡影响范围大,滑坡土体的体积较大.

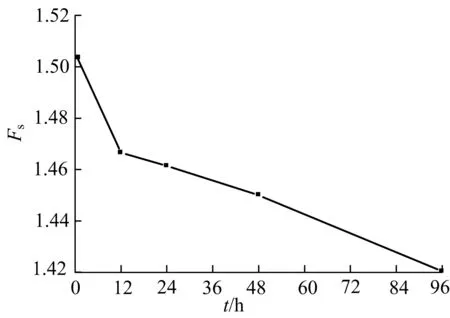
图7 安全系数随降雨历时变化Fig.7 Safety coefficient with the rainfall duration change

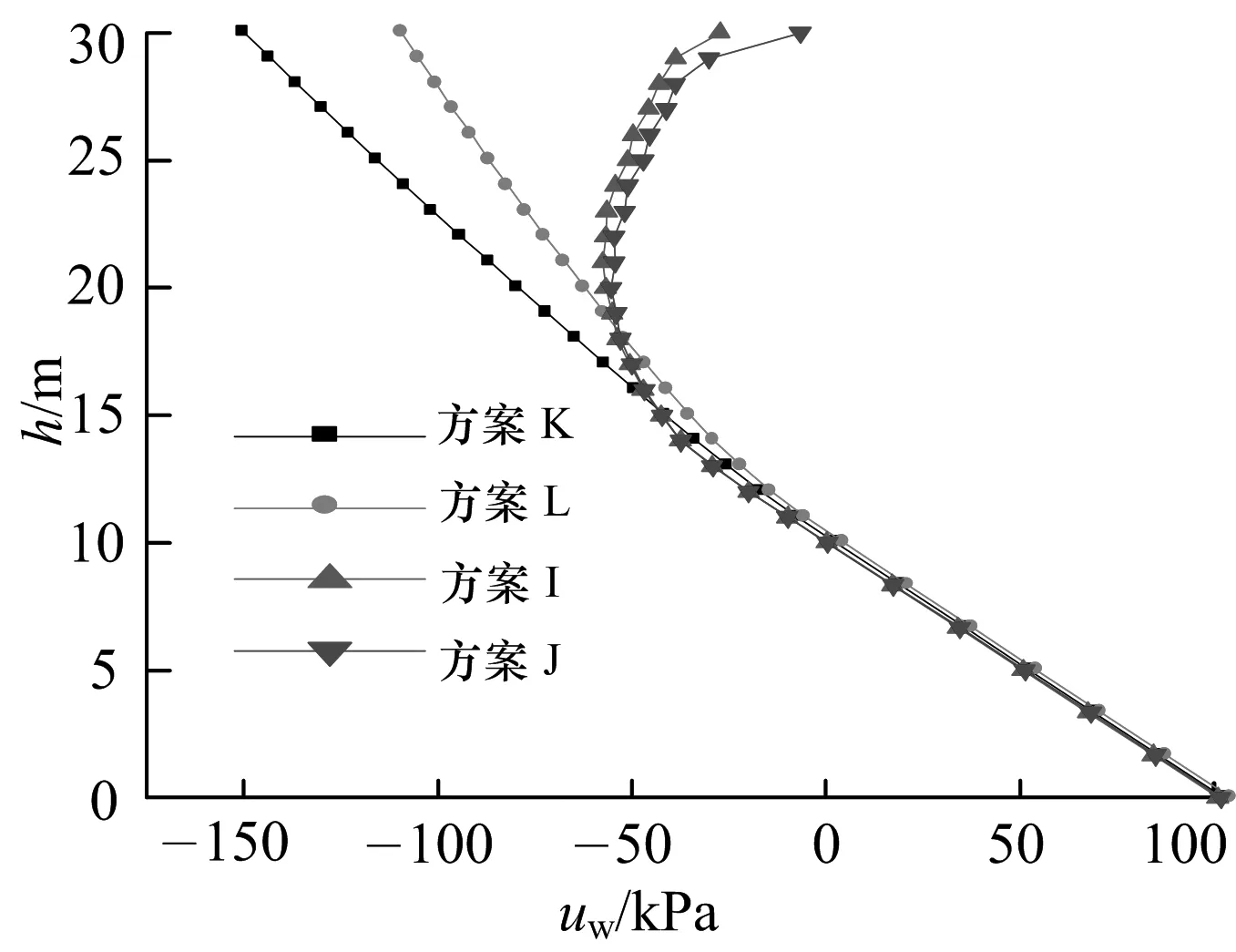
图8 短时强雨、长时弱雨,孔隙水压力随高程变化对比Fig.8 Short-term strong rainfall and long weak rainfall, pore water pressure comparison chart with elevation changes

由图9,10对比分析可知,在饱和渗透系数一定时,无论短时强降雨还是长时弱降雨,在降雨结束时,边坡安全系数都大幅的降低.在降雨停止后随着时间的推移,入渗到土体内的雨水开始蒸发或由坡面向外渗出,边坡内的孔隙水压力开始减小,基质吸力增大,导致边坡安全系数又逐渐的升高.由于水分消散的速度由快到慢,安全系数上升的幅度也由大到小,最后基本维持在一个定值,在一定的时间之内不能恢复到雨前初始状态的安全系数大小.说明了降雨时间间隔的长短对于安全系数的恢复程度有直接地影响,可见降雨时间间隔对边坡的稳定性十分重要.

图9 短时强降雨下,安全系数随时间的变化Fig.9 Short-term strong rainfall, the safety coefficient changes with time

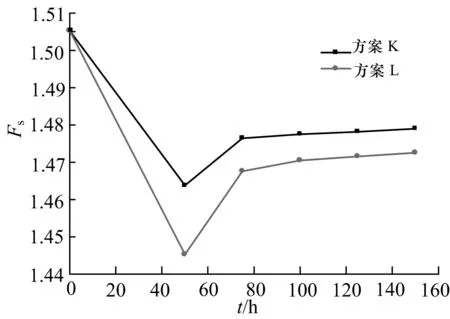
图10 长时弱降雨下,安全系数随时间的变化Fig.10 Long weak rainfall, the safety coefficient changes with time

同时,对比短时强降雨与长时弱降雨方案下土体边坡安全系数大小可知,短时强降雨停止时安全系数较长时弱降雨停止时的安全系数更低.其原因是短时强降雨方案下,降雨强度大于土体的饱和渗透系数而产生地表径流,虽然有一部分雨水并没有渗入到边坡内,但是该部分雨水将随着边坡坡面产生顺坡流动,顺坡流动会对边坡上部土体产生较大的冲刷作用,进一步对边坡的稳定产生不利的影响,边坡的稳定安全系数又会再次降低.

5 结论

通过以上算例分析可知降雨要素对土质边坡稳定性的影响巨大.降雨强度和降雨历时的增加都会导致边坡的安全系数降低,产生不利影响;短时强降雨下雨水入渗较浅可是孔隙水压力改变较大,而长时弱降雨下孔隙水压力改变较小可是雨水入渗较深,两种情况都会是边坡的稳定性大幅降低.

文中提到饱和渗透系数的大小与降雨时间间隔的长短也会对降雨下的边坡稳定性产生影响,这方面可以作为后续研究的方向.

参考文献(References)

[1] 吴梦喜,高莲士.饱和-非饱和土体非稳定渗流数值分析[J].水力学报,1999,12:38-42.

Wu Mengxi, Gao Lianshi.Saturated-unsaturated unsteedy seepage numerical analysis[J].JournalofHydraulicEngineering,1999,12:38-42.(in Chinese)

[2] 毛昶熙,段祥宝,李祖贻.渗流数值计算与程序应用[M].江苏南京:河海大学出版社,1999:3-40.

[3] 顾慰慈.渗流计算原理及应用[M].北京:中国建材工业出版社,2000:10-22.

[4] 吴林高,缪俊发,张瑞，等.渗流力学[M].上海:上海科学技术文献出版社,1996:150-207.

[5] 朱军.饱和非饱和三维多孔介质非稳定流分析[J].武汉大学学报:工学版,2001,34(3):5-8.

Zhu Jun.Saturated-unsaturated unsteady seepage analysis of porous medium[J].EngineeringJournalofWuHanUniversity,2001,34(3):5-8.(in Chinese)

[6] D G弗雷德朗德,H 拉哈尔佐.非饱和土力学[M].北京:中国建筑工业出版社,1997,8:392-405.

[7] 赵慧丽,马易鲁.非饱和土抗剪强度研究方法的探讨[J].岩土工程技术,2001(3):142-145.

Zhao Huili,Ma Yilu.Discussion on research method of strength of unsaturated soil[J].GeotechnicalEngineeringTechnique,2001(3):142-145.(in Chinese)

[8] 陈祖煜.土质边坡稳定分析[M].北京:中国水利水电出版社,2003:121-147.