喷射混合器放大效应的计算流体力学模拟
张 妍,胡仰栋,伍联营
(中国海洋大学化学化工学院,山东 青岛 266100)
化工生产的大规模化必然要求生产装置的大型化。一般一项大化工技术的成熟需要经历小试、中试和工业化示范等逐级放大阶段,这主要是为了解决装置规模化后产生的放大效应。由于放大效应的存在使得化工生产的大规模化存在很大风险,所以分析和解决放大效应对实现生产大规模化具有重要意义。通常可直接采用实验手段研究反应设备的放大效应[1,2]。近年来随着计算机应用水平的提高,采用以计算机为基础的放大方法,个别工艺可以从小试直接放大到工业生产规模。其中,计算流体力学(CFD)方法的发展使研究反应设备的放大效应更为便利[3,4]。喷射器是一种高效的混合设备,利用工作流体的高速流动卷吸次流流体。和传统混合设备相比,其结构简单、内部无运动部件、传质效率高,在石油和化工等工业中应用广泛。喷射器的结构参数对其性能影响非常显著,许多学者对喷射器的结构参数进行了研究。马连湘等[5,6]研究表明,喷射反应器的喷嘴/混合段直径比对转化率和混合效果影响显著。Balamurugan 等[7,8]进行气液喷射器模拟,发现存在一个最佳面积比使得引射流体的卷吸率达到最佳。Zhu 等[9]研究表明,存在一个最佳混合段收敛角度使得喷射器性能达到最佳。现有研究主要集中在局部结构的扩大或缩小对喷射器性能的影响,且大多针对气-液喷射器和固-液喷射器[10,11],将喷射器整体进行放大研究的文献较少。本工作采用流体力学计算软件Fluent6.3,通过计算机模拟对液-液喷射器进行放大,主要针对喷射器放大后产生的放大效应,预测放大后喷射器内的湍动状况及混合性能的变化,为喷射混合器规模化设计提供参考。
1 数值模拟部分
1.1 物理模型
喷射器的主要结构包括喷嘴、吸收段、混合段和扩散段,结构如图1所示。本模拟所用的喷射器基本尺寸为喷嘴直径3 mm,混合段直径6.5 mm,长度18 mm。利用Fluent 前处理软件Gambit 建立3 维流动模型,采用分区划分、结构化与非结构化网格相结合的网格划分方式,同时在壁面处以及喷嘴处进行网格加密,全面考虑了喷射器的几何结构,使得模拟更加符合喷射器的实际情况。

图1 喷射混合器结构Fig.1 Schematic diagram of the ejector
1.2 湍流模型
采用Realizablek-ε模型对喷射器进行模拟。当流体不可压缩时,Realizablek-ε模型中关于k和ε的方程为:

1.3 边界条件
喷射器的两个进口均采用速度入口(velocity-inlet)边界条件,射流流速为16.8 m/s,引射流速为3.7 m/s;出口采用流动充分发展的压力出口(pressure-outlet)边界条件,静压值为1.825 MPa;壁面采用无滑移边界条件及标准壁面函数,所涉及的湍流强度(I)按照以下经验关系计算:

模拟过程所选用的两股物料分别从主流口和次流口进入,主流口进料物质A 的密度为1 163 kg/m3,粘度为0.000 338 kg/(m·s),次流口进料物质B 的密度为1 155.2 kg/m3,粘度为0.001 1 kg/(m·s)。模拟时对流项的离散格式采用二阶迎风格式,压力项采用Standard 格式;压力-速率的耦合问题采用SIMPLE 算法,并采用稳态求解器进行迭代计算,当各变量的残差达到10-4可视为已经收敛。
1.4 网格无关性检验
在相同模型与边界条件下,对初始尺寸和放大10 倍后的喷射器做了3 种尺寸的网格划分,比较不同网格尺度下组分B 的质量分数沿中心轴线方向的分布,见图2。

图2 不同网格下中心轴向B 组分的质量分数Fig.2 The mass fraction of material B along the axial line at different grid scale
由图2可见,不同网格尺度下组分B 的质量分布基本一致,证明了模拟结果与网格数无关。依照相同的方式,对其他放大倍数下的喷射器进行网格无关性检验。下述模拟结果均为验证网格无关性之后的。
2 模拟过程与结果分析
2.1 模型验证
采用毕荣山[12]所研究的喷射器湍流混合的PLIF 实验结果作为验证实例,模型验证时所采用的喷射器的基本结构尺寸:主流口与次流口直径分别为10 mm 和8 mm,出口直径25 mm,喷嘴直径3 mm,混合段直径6.5 mm,混合段长度3 mm,扩散段角度3°。按相同的条件,同时考虑存在一定误差,模拟了两进口流速同时增加5%的情况,次流口进料组分的质量分数沿中心轴线的分布见图3。Computational 1,2 和3 分别为实验流速、流速提高5%及文献中的模拟结果,本工作所模拟的喷射器内压降与实验所用喷射器内的压降均在0.2 MPa 左右。结果表明,模拟与实验结果分布规律相同,存在一定差异但都在可接受的误差范围内。说明该模型可适用于喷射器的模拟。
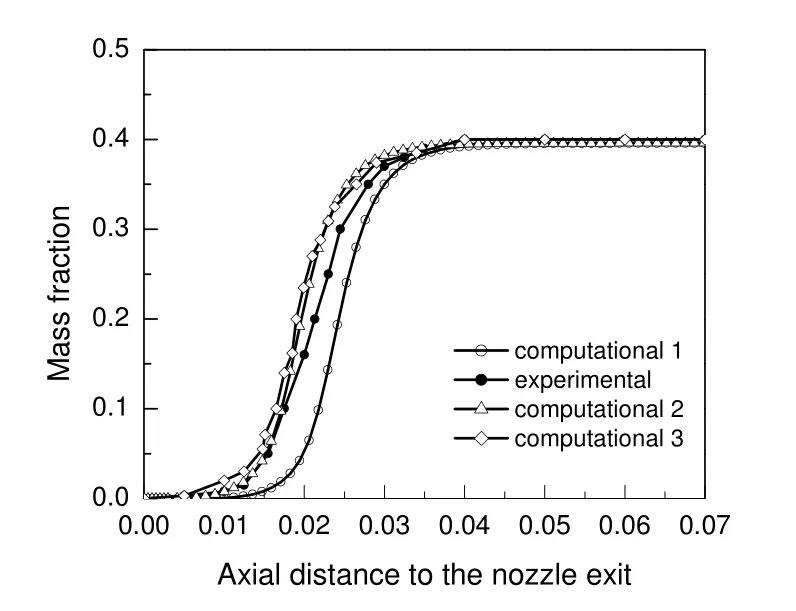
图3 质量分数沿中心轴线的分布Fig.3 The mass fraction along the axial line
2.2 有扩散角度的喷射器的放大效应及分析
为研究喷射混合器的放大效应,保证射流及引流速度不变,同时扩散段角度不变,按照几何相似的原则,喷射器的尺寸分别放大3,5,8 和10 倍,对应的处理量分别扩大9,25,64 和100 倍,建立模型并模拟分析。从分析流动状况入手,研究放大后喷射器内速度场、湍动能、湍流耗散率、涡量以及质量分数等参数变化,即产生的放大效应,并分析放大后流动状况和混合性能的改变。
2.2.1 速度分布与湍动能
图4为放大前后速度沿中心轴向的分布,轴向距离用无量纲距离即实际距离与总长度之比来表示。从图中可以看出,不同放大倍数的喷射器,速度沿轴线方向上的分布趋势基本一致。图5为放大前后湍动能沿中心轴向的分布,放大前后轴向湍动能的分布也基本一致。因此,喷射器的放大对速度场以及湍动能的分布无明显影响。

图4 喷射器内速度沿中心轴线的分布Fig.4 The velocity magnitude along the axial line
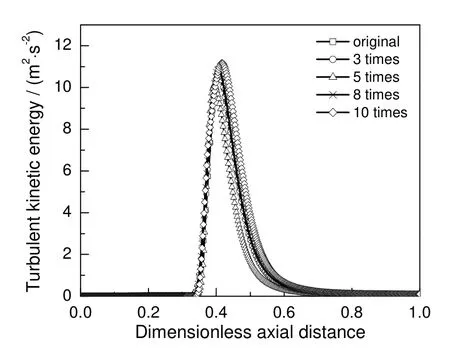
图5 喷射器内湍动能沿中心轴线的分布Fig.5 The turbulent kinetic energy along the axial line
2.2.2 湍流耗散率
湍流耗散率(ε)是指单位时间内损耗的湍动能,表示在分子粘性力的作用下,通过摩擦不断地将湍动能转化为分子运动的动能,造成湍动能的耗散。其定义式为:

湍流耗散率是评价流体流动湍动程度的非常重要的参数,数值越大表示湍动性能越好。喷射器作为混合设备,两股进料在混合段内相遇,流体微团的高频脉动造成湍动能的耗散,利于流体分散,从而强化混合。图6为放大不同倍数的喷射器内湍流耗散率沿中心轴线的分布。从图中可以看出,放大前后湍流耗散率的分布趋势基本相同,分布在湍流核心的周围。但是在数值上,随着喷射器尺寸的放大湍流耗散率显著降低,反映出放大后喷射器内部湍动减弱,物料的混合有明显下降。
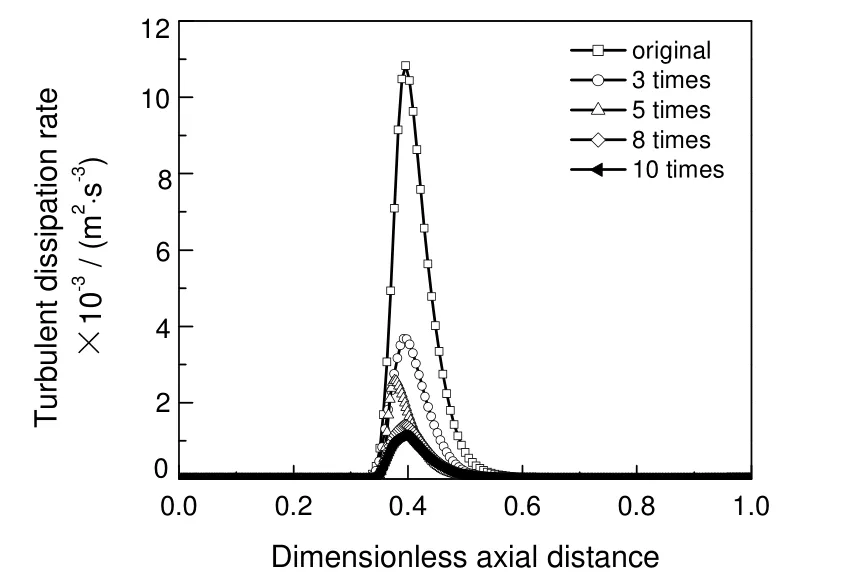
图6 喷射器内湍流耗散率沿中心轴线的分布Fig.6 Turbulent dissipation rate along the axial line

图7 喷射器内涡量沿中心轴线的分布Fig.7 Vorticity along the axial line
考察喷射器中心轴线方向上湍流耗散率的最大值与喷射器放大倍数的关系时,发现放大前和放大不同倍数的喷射器对应的中心轴线方向湍流耗散率的最大值分别为10 827,3 674,2 586,1 407 和1 146 m2/s3,喷射器中心轴向湍流耗散率最大值与放大倍数近似成反比。可见,喷射器放大后湍流耗散率变化显著,放大后流体流动的湍动减弱,不利于混合。
由伯努利方程分析可知,在忽略机械能损失的条件下,由于喷射器放大前后进出口的流速相等,因此进出口压差(△p)相等,即输入的单位体积的净能量相等。然而对于大处理量(V)的喷射器来说,输入的总的净能量(△p·V)要大于小处理量的喷射器,而湍流耗散率却降低,这和喷射器内湍流的流体微团运动有关。因此本工作考察了放大前后喷射器内涡量的变化。
涡量(ω)是描述流体微团旋转运动的旋度。湍流场是由涡量不同的涡旋叠加而成,涡量越大,表示流体旋转运动越强,高频脉动越剧烈,湍动程度越大,造成湍动耗散的增强,利于混合。图7比较了不同放大倍数的喷射器内涡量沿中心轴线的分布。可以看出,喷射器放大后,涡量数值明显降低,表示放大后喷射器内流体微团旋转运动强度降低,湍动程度下降,进而导致湍流耗散率的降低。同时放大后旋涡尺度增加,湍流的高频脉动降低。因此,喷射器放大后流场的湍动状况发生改变。
另外,由湍流耗散率近似计算式:

式中:Cμ为0.09。对于充分发展的湍流,其值为水力直径的0.07 倍。由2.2.1 中得出k基本不变,而湍流长度尺度随着喷射器结构尺寸的放大而成比例增加,根据近似计算式亦可得出湍流耗散率与放大倍数近似反比的关系。
2.2.3 混合情况
物料经喷嘴进入喷射器后,主要在混合段完成混合。当物料的质量分数达到均一时,可认为完成了混合过程。表1为不同尺寸喷射器内完成混合时所需的实际距离及无量纲距离,由上述分析可知,随着喷射器的放大,湍流耗散率及涡量等降低,不利于物料的混合,导致达到完全混合状态所需的实际距离增加,与喷射器放大倍数成正比。然而对于无量纲距离,随着喷射器的放大,数值基本保持不变。

表1 完成混合所需要的距离Table 1 The distance required for mixing completely
2.3 扩散角为0°的喷射器的放大效应及分析
混合段和扩散段是喷射器的主要结构,两股流体主要在混合段内完成混合。流体从混合段进入扩散段,动能转化为压力能。当取消扩散段的角度,忽略该能量转化过程,将原有的混合段与扩散段组成一个大的混合段,此时喷射器内的压降同有扩散角度的喷射器相比有所增加。对于这种喷射器,在射流及引流速度不变的条件下,按照几何相似的原则,分别放大3,5,8 和10 倍,建立模型并模拟,考察无扩散角度的喷射器的放大效应。
2.3.1 速度分布与湍动能
喷射器放大后速度场及湍动能的分布无明显变化。此结果与有扩散角度喷射器的模拟结果一致。
2.3.2 湍流耗散率
对于扩散角度为零的喷射器,放大不同倍数后喷射器内湍流耗散率的分布趋势基本相同,数值随着喷射器尺寸放大倍数的增加而减小,由于喷射器的放大,喷射器内的湍动情况下降,不利于混合。该结论与有扩散角度的喷射器模拟结果相同。图8为喷射器中心轴向湍流耗散率最大值随放大倍数的变化曲线,将有、无扩散角度的喷射器分别设为Type A 与Type B。图中直观的反映出中心轴线方向上湍流耗散率的最大值随着喷射器的放大而减小。喷射器放大前、与放大3,5,8 和10 倍对应的中心轴线方向湍流耗散率的最大值分别为8 873,3 136,2 319,1 184 和948 m2/s3,与喷射器尺寸的放大倍数存在反比例关系。由此可以看出,喷射器放大后湍流耗散率的变化显著。

图8 中心轴向湍流耗散率最大值与放大倍数的关系Fig.8 The maximum of axial turbulent dissipation rate versus scale-up factor
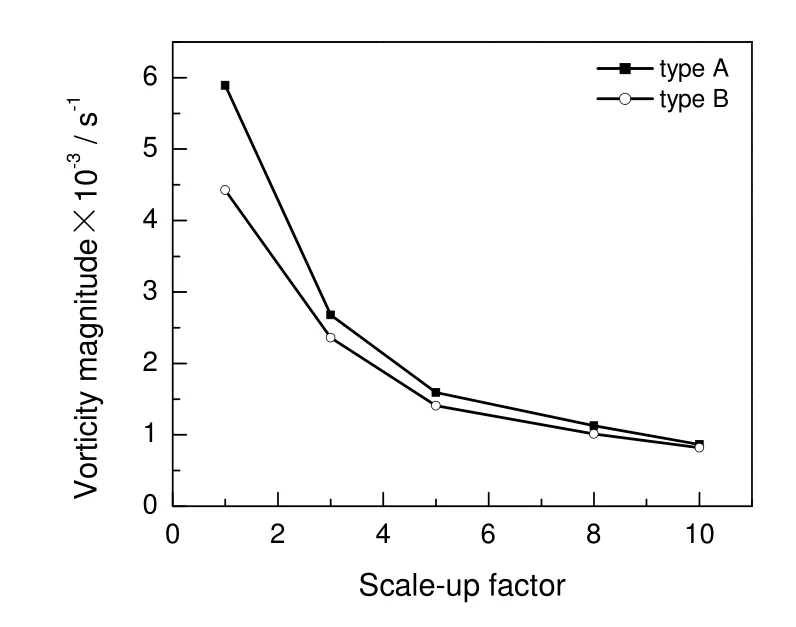
图9 中心轴向涡量最大值与放大倍数的关系Fig.9 The maximum of axial vorticity versus scale-up factor
图9为两种喷射器中心轴向涡量最大值随放大倍数的变化图。对于无扩散角度的喷射器,放大后喷射器内的涡量数值降低,说明混合器内的湍流旋涡尺度较大,湍流脉动远不及小规模喷射器,因此放大后的湍流耗散率下降,不利于混合。这与有扩散角度的喷射器的放大研究的结论相同。
2.3.3 混合情况
表2为不同尺寸喷射器内完成混合时离喷嘴的距离。由于湍流耗散率及涡量随喷射器的放大而减小,导致混合性能的下降而造成完成混合所需要的实际距离增加,并且与喷射器放大倍数成正比,而完成混合的无量纲距离数值上略有变化。此结果与有扩散角度喷射器的模拟结果基本一致。

表2 完成混合所需要的距离Table 2 The distance required for mixing completely
3 结 论
应用Fluent 软件对喷射器进行了模拟并进行了放大研究,考察并分析了喷射器内速度、湍动能、湍流耗散率和涡量等指标随着喷射器的放大的变化情况,即喷射器放大后产生的放大效应,得出以下结论:
a)对于存在扩散角度的喷射器,放大后速度与湍动能的变化不大,而喷射器的放大效应主要体现在湍流耗散率与涡量的变化之上。喷射器尺寸放大10 倍后,中心轴线方向湍流耗散率的最大值从10 827 变到1 146 m2/s3,轴线方向上涡量最大值从5 894 变到865 s-1;同样,对于无扩散角度的喷射器,喷射器内速度和湍动能分布基本不随喷射器的放大而改变,而湍流耗散率与涡量的数值随着喷射器的放大而降低,这与存在扩散角度的喷射器的模拟结论相同。
b)对于两种不同的喷射器,放大后湍流耗散率及涡量降低,表明喷射器内的湍动性能随着喷射器的放大而降低,不利于混合,造成完成混合过程所需要的实际距离随着喷射器的放大而增加,而无量纲距离变化不大。
符号说明
C——湍流模型中的经验常数
I——湍流强度
Re——雷诺准数
u, u’——分别为流体流速、脉动速度,m/s
V——处理量,m3/s
σ——湍流方程的普朗特数
k——湍动能,m2/s2
l——湍流长度尺寸,m
ε——湍流耗散率,m2/s3
ρ——流体密度,kg/m3
μ,μt——分别为粘度、湍流粘度,Pa/s
ω——涡量,s-1
[1]黄雄斌, 闫宪斌, 施力田, 等.固液搅拌槽内液相速度的分布[J].化工学报, 2002, 53(7):717-722.Huang Xiongbin, Yan Xianbin, Shi Litian, et al.Liquid velocity distributions in solid-liquid stirred vessels[J].Journal of Chemical Industry and Engineering, 2002, 53(7):717-722.
[2]纪风翰, 龚绍英.液-固相釜式搅拌反应器的放大研究[J].化学反应工程与工艺, 1997, 13(3):290-297.Ji Fenghan, Gong Shaoying.The scale-up research of the liquid-solid stirred-tank reactor[J].Chemical Reaction Engineering and Technology, 1997, 13(3):290-297.
[3]Li M Z, White G, Wilkinson D, et al.Scale up study of retreat curve impeller stirred tanks using LDA measurements and CFD simulation[J].Chemical Engineering Journal, 2005, 108:81-90.
[4]Wang X, Ding J, Guo W Q, et al.Scale-up and optimization of biohydrogen production reactor from laboratory-scale to industrial-scale on the basis of computational fluid dynamics simulation[J].International Journal of Hydrogen Energy, 2010, 35:10960-10966.
[5]马连湘, 毕荣山, 郑世清.结构参数对液液喷射反应器性能的影响[J].化学工程, 2008, 36(12):133-36.Ma Lianxiang, Bi Rongshan, Zheng Shiqing.Effect of geometric parameters on performance of liquid-liquid jet reactors[J].Chemical Engineering, 2008, 36(12):133-36.
[6]毕荣山, 谭心舜, 林柯利, 等.结构尺寸对液-液喷射器湍流混合性能的影响[J].高校化学工程学报, 2010, 24(5):752-757.Bi Rongshan, Tan Xinshun, Lin Kel, et al.The effect of configuration dimension on turbulent mixing in liquid-liquid ejectors[J].Journal of Chemical Engineering of Chinese Universities, 2010, 24(5):752-757.
[7]Balamurugan S, Gaikar V G, Patwardhan A W.Effect of ejector configuration on hydrodynamic characteristics of gas-liquid ejectors[J].Chemical Engineering Science, 2008, 63:721-731.
[8]Kandakure M T, Gaikar V G, Patwardhan A W.Hydrodynamic aspects of ejectors[J].Chemical Engineering Science, 2005, 60:6391-6402.
[9]Zhu Y H, Cai W J, Wen C Y, et al.Numerical investigation of geometry parameters for design of high performance ejectors[J].Applied Thermal Engineering, 2009, 29:898-905.
[10]Jadhav S V, Pangarkar V G.Partical-Liquid mass transfer in three-phase sparged reactors:Scale-up effects[J].Chemical Engineering Science, 1991, 46(4):919-927.
[11]姚 云.喷射器内气液流动与混合性能的研究[D].青岛:青岛科技大学, 2009.
[12]毕荣山.高Schmidt 数下喷射器内湍流反应的实验研究和多尺度模拟[D].青岛:青岛科技大学, 2008.

