气固流化床分布板区流动特性

陈伟博，程中虎，房倚天

(1.中国科学院山西煤炭化学研究所，山西 太原 030001；2.中国科学院大学，北京 100039)

气固流化床具有良好的传质、传热性能，广泛应用于石油化工、煤化工等工业领域。在设计流化床时，经常遇到的一个问题是如何预测分布板上方气固流动行为。气固流化床中分布板上方，孔射流深度以下的分布板区对整个流化床的气固流动、传质传热和反应过程有着重要的影响。Behie 等[1,2]提出了分布板区反应模型，发现流化床反应器中快速反应大部分是在分布板区完成的。射流是气体进入流化床后形成的空穴，在射流边界，气体对固体颗粒有着强烈的夹带作用，对颗粒的流动和磨损有着较大影响。在射流顶端，气泡与射流分离，气泡初始大小的研究对气泡行为的预测有很大的帮助。分布板区的研究对分布板的设计和气固流化床内气固流动的认识都有重要意义。在描述流化床气固流动行为时，射流是一个重要的研究对象。对射流的研究主要集中在两种类型的射流：一种是在流化床中独立于分布板的射流管产生的射流。Merry[3]研究了2 维床中的射流，提出了垂直射流深度的经验关联式；Yang 等[4]在总结了2 维和3 维流化床中单孔和多孔射流数据后，提出了以两相Froude 数为基础的射流深度关联式；Guo 等[5,6]对射流流化床中的射流深度进行了研究；Sauriol 等[7]研究了圆柱床中不同方向的射流管产生的射流，发现分布板流化风量会对射流管的射流产生影响。另一种是分布板区射流。分布板区主要分为射流区、颗粒运动区和死区。Wen 等[8]在2 维床和圆柱床中研究了颗粒死区，提出了消除颗粒死区所需气量的经验关联式。Horio 等[9]提出了分布板区的模型，并得到了颗粒运动区直径和死区高度的经验关联式。Müller 等[10,11]采用MRI（Magnetic Resonance Imaging）研究了圆柱床中分布板区射流，得到了射流的3 维图像，并分别提出了射流深度计算公式。Agarwal 等[12]采用PIV（Particle Image Velocimetry）和DIA（Digital Image Analysis）研究2 维流化床中分布板区，发现在Uo/Uomf2D为1左右，射流的发展是不一致的，因此，将射流深度计算公式分为了两部分。对分布板区的研究可为流化床的设计和操作提供重要的参考，为了进一步了解分布板对流化床内气固流动的影响，本工作利用摄像法，采用多种分布板和颗粒，对流化床分布板区进行研究，提出了新的射流深度和死区高度经验关联式。

1 实验部分

实验装置如图1所示。实验设备主要有鼓风机，转子流量计，2维流化床，摄像机和计算机。实验中使用的2 维床宽200 mm，厚15mm，分布板结构如图2所示。为了观察，射流分布板孔距离床板面2 mm，P为相邻两个孔的孔间距，床体、分布板和气室通过法兰连接。实验中所使用的分布板结构参数见表1。实验中采用了聚苯乙烯颗粒、高粱米颗粒和绿豆颗粒，颗粒物性见表2。

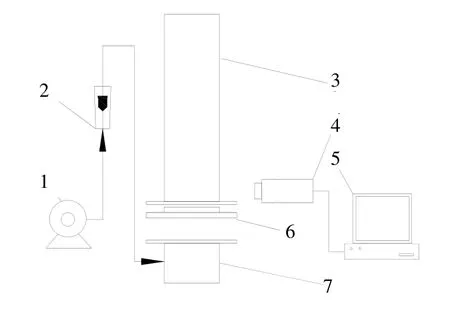
图1 实验装置Fig.1 Experimentsetup

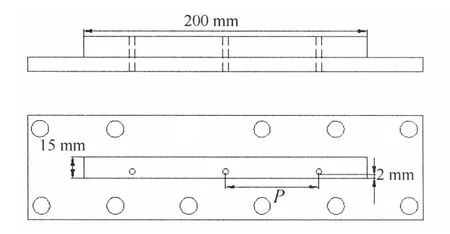
图2 分布板结构Fig.2 Schematic of distributor plate

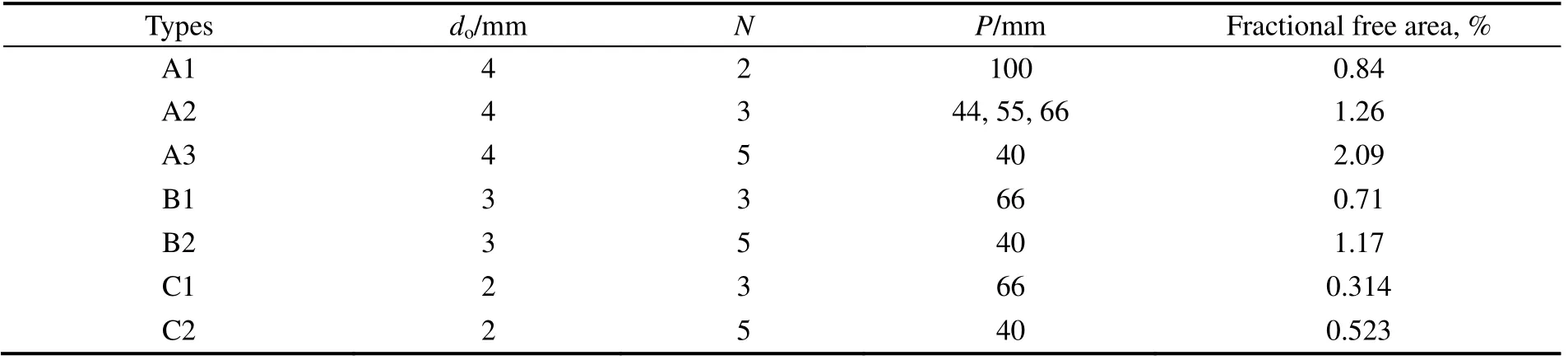
表1 分布板结构参数Table 1 Structure parameters of distributor plates

表2 颗粒物理性质Table 2 Physical properties of testedfluidized be d media

Filla 等[13]总结了射流的发展，如图3所示。本实验的射流深度（Lj）定义沿用了Filla 的定义，即以射流顶端气泡分离前，射流颈部的高度为射流深度。

图3 流化床中气体射流Fig.3 Schematic of gasinjection in fluidized bed

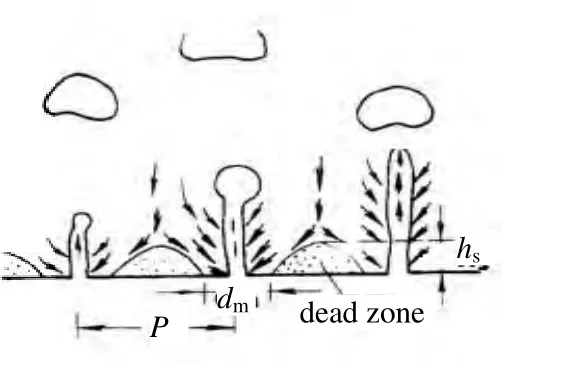
图4 分布板区结构模型Fig.4 Model of grid zone

Horio等[9]根据研究分布板上方颗粒运动作了死区和颗粒运动区模型，如图4所示。

实验中采用摄像法，在不同的操作条件下，用摄像机录制每秒25 帧的视频，并存储于计算机中，再对视频进行逐帧分析来获取实验数据。流化床分布板上方贴有最小网格为10 mm×10 mm 的坐标纸，底部和边壁贴有坐标纸，以确定射流深度、颗粒运动区直径和死区高度。

2 结果与讨论

2.1 孔速对射流深度的影响

图5为使用不同分布板时，孔速（Uo）对Lj的影响。对于3 种不同孔径的分布板，射流深度都随着孔速的增加而增大，这是由于射流气体的动量随孔速的增加而增大造成的。从图5可以看出，孔径相同时，不同孔数的分布板在相同的孔速下，射流深度不同，孔多的分布板的射流深度要大，这与Müller等[10]采用MRI在圆柱床中观察到的结果一致。Guo 等[5,6]在研究射流流化床射流深度时，发现流化风量对Lj是有影响的。在实验中，在相同的孔速下，不同孔数分布板所对应的流化风量是不同的，造成了分布板上方颗粒流化状态的差异，是导致孔数多的分布板产生的射流深度较大的原因。因此，本工作在拟合射流深度计算公式时，用U/Umf表示床层流化状态对射流深度的影响。

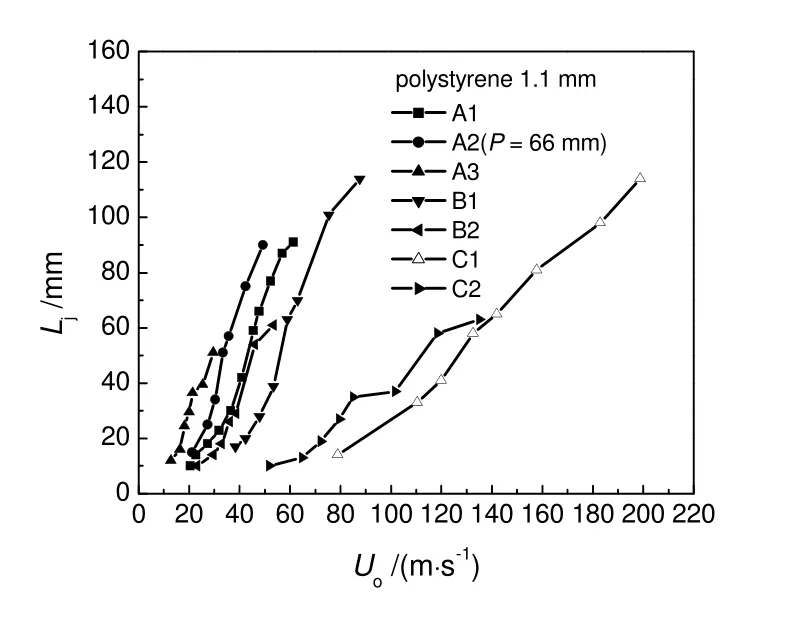
图5 不同分布板时Uo 对Lj 的影响Fig.5 Influence of orifice velocity on jet penetration length for different distributors

2.2 分布板孔径对射流深度的影响

图5考察了分布板孔径对射流深度的影响，从图中可以看出，在相同的孔速下，射流深度随着孔径增加而增大，这是因为在相同的孔速下，气体动量随着孔径的增加而增大。为了观察表观气速对不同孔径分布板的射流深度的影响，采用U/Umf作为横坐标，如图6所示。从图中可以看出：射流深度随着U/Umf的增加而增大；当U/Umf≤1 时，不同孔径的分布板的射流深度基本相同；当U/Umf＞1时，不同孔径的分布板的射流深度才出现了相对明显的差别。

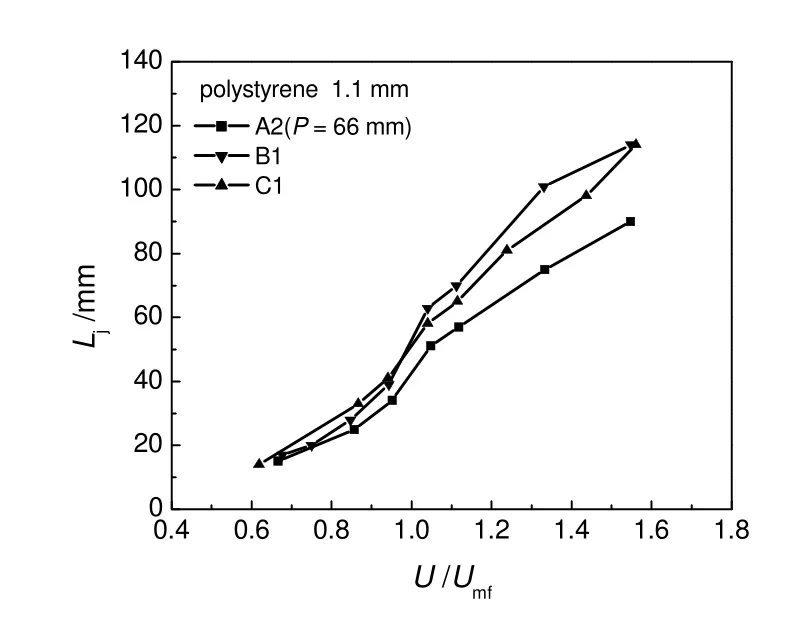
图6 不同分布板时U/Umf 对Lj 的影响Fig.6 Influence of U/Umf on jet penetration length for different distributors

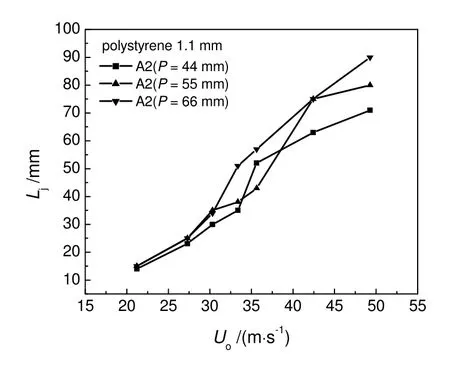
图7 不同孔间距分布板时Uo 对Lj 的影响Fig.7 Influence of orifice velocity on jet penetration length for distributors with different orifice pitch

2.3 分布板孔间距对射流深度的影响

实验考察了分布板孔间距对射流深度的影响。结果如图7所示。为了考察不同孔间距对射流深度的影响，采用不同孔间距的A2 分布板进行研究。从图中可以看出，在孔速相对较低时，不同孔间距的分布板产生的射流深度基本相同。孔间距对射流深度的影响只有在孔速较大时才能表现出来，而且孔间距大的分布板产生的射流深度较大。这是由于当孔速小时，分布板上方射流之间不会相互影响，因此，当孔速相同时，不同孔间距的分布板的射流深度基本相同。孔速较大时，相邻的射流会相互影响甚至在射流顶端发生合并，合并使射流的颈部降低，孔间距对射流合并时的孔速影响很大，孔间距小的分布板发生射流合并时的孔速较低，当Uo为42.4m/s 时，P为44 mm 的分布板上方的射流已经在顶端合并，P为55 mm 和P为66 mm 的分布板上方的射流没有合并，造成了孔间距大的分布板的射流深度较大。

2.4 颗粒物性对射流深度的影响

考察了颗粒物性对射流深度的影响，结果如图8所示。由图可知，3 种不同物性的颗粒，在相同的孔速下，密度和粒径大的颗粒的射流深度要比小的颗粒的小。Zhong 等[6]认为射流气体和床层颗粒之间的性质差异会阻碍射流的发展，颗粒密度越大，气体和颗粒的性质差异就越大，气体动量消散地就越快。另外，随着颗粒直径增加，床层粘度增大，当气体经过颗粒时，需要克服更大阻力而造成动量损失。在图9中，以U/Umf作为横坐标，可以看出，在相同的U/Umf下，3 种颗粒的射流深度基本相同。

图8 不同物性颗粒时Uo 对Lj 的影响Fig.8 Influence of orifice velocity on jet penetrationlength for different kinds of particles

2.5 射流深度计算公式

表3列出了文献中常见的射流管射流和分布板区射流的射流深度计算公式。

表3 文献中射流深度公式Table 3 Correlations of jet penetration length from literature

在拟合射流深度计算公式时，Blake 等[15]认为影响射流深度的主要的4 个无因次数分别为Stokes数（ρpUodp2/μdo），Froude 数（Uo2/gdo），Reynold 数（ρpUodp/μf）和气固密度比（ρf/ρp），其中Froude数是一个重要的无因次数。Yang[4]的公式采用了两相Froude 数，Rees 等[11]研究了圆柱床中分布板射流，并引入了do2/Ao，以考虑不同孔结构分布板对射流深度的影响，Agarwal 等[12]研究了2 维流化床中分布板射流，发现在最小流化气速上下射流深度随孔速的变化规律不同，提出在最小流化气速上下，采用不同的射流深度计算公式。

图10为射流深度计算公式预测值与实验值的对比。发现Yang 的公式预测值远远大于实验值和其他公式的预测值。在较低孔速下，其他两个公式对射流深度的预测值与实验值较为接近，但在高孔速下，这些公式的预测值要小于实验值，Agarwal 的公式虽然提出了最小流化气速之上的射流深度计算公式，但预测值仍然比实验值小。从以上不同因素对射流深度的影响可以看出，床层所处的流化状态对射流深度影响较大。在本研究中，以U/Umf表示流化状态对射流深度的影响，根据前人研究结果使用Froude 数，并使用dp/do。利用这些无因次数对实验数据进行拟合，得到了以下公式：

图10 射流深度实验值与公式预测值的对比Fig.10 Comparison of experimental data with calculated data of jet penetration length

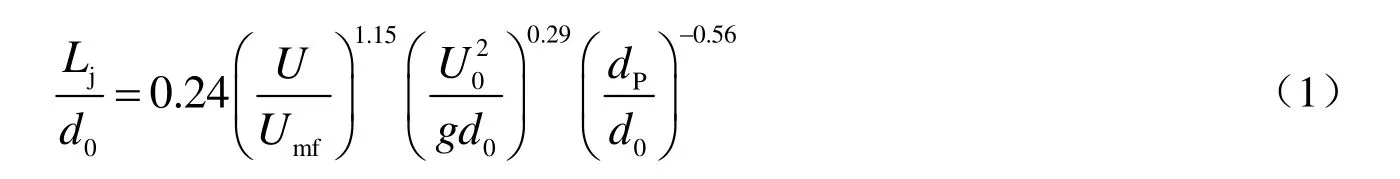
图11对比了使用不同分布板时射流深度的实验值与公式（1）的预测值。对A2 和A3 分布板，公式（1）的预测值和实验值能很好吻合；对A1 分布板，低气速时，预测值和实验值能很好吻合，气速较高时，预测值要低于实验值，偏差在40%以内。表明公式（1）能较好地预测不同类型分布板的射流深度。

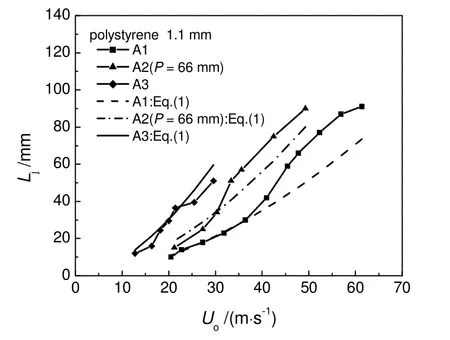
图11 射流深度实验值与Eq(1)预测值对比Fig.11 Comparison of jet penetration length from Eq(1) with experimental data

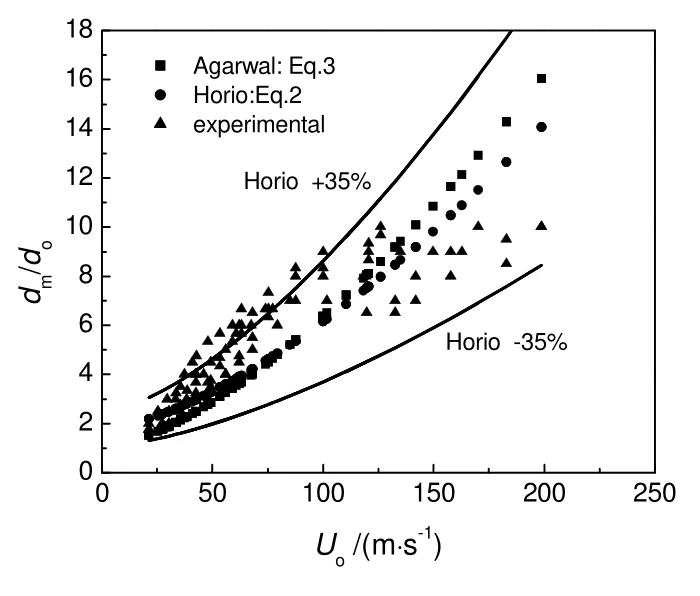
图12 dm/do 的实验值与公式预测值对比Fig.12 Comparison of dm/do from Eqs (2) and (3) with experimental data

2.6 颗粒运动区直径

Horio 等[9,12]都认为，颗粒运动区直径（dm）只与do和Uo有关，公式（2）和（3）分别为Horio等得到的关联式。图12为实验中dm与公式（2）和（3）得到的预测值的比较，从图中可以看出，实验值大部分都在预测值的±35%以内。

2.7 死区高度

死区即分布板孔之间颗粒不流化的区域，死区的存在会对反应器，特别是有快速、强放热反应的反应器的操作带来影响。由于死区颗粒基本不流动，在这个地区的传质传热很慢，容易形成局部高温。

图13为使用不同孔间距的分布板时hs随孔速的变化。随着孔速的增加，射流周围颗粒的运动范围变大，从而使hs不断减小。在相同的孔速下，随着孔间距的增大，hs显著增大。

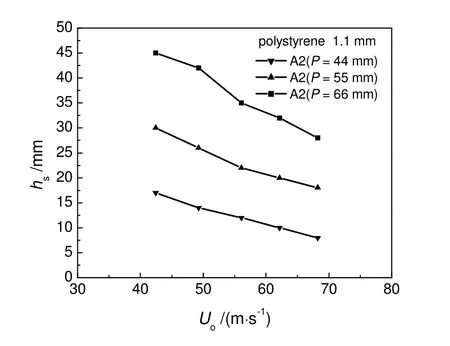
图13 Uo 对hs 的影响Fig.13 Influence of orifice velocity on dead zone height

图14 死区高度的实验值与公式（5）预测值对比Fig.14 Comparison of dead zone height from Eq(5) with experimental data

Horio 等[9]根据死区几何模型，提出了hs与dm的关系式：

Horio 等认为死区颗粒角度（φ）和颗粒休止角（φr）相近，实验发现φ与φr有较大差异，这与Thorpe 等[16]的研究一致。Agarwal 等[12]用φ代替了公式（4）中的φr，但φ不易确定，虽然能够通过公式（2）或公式（3）估算出dm的值，但hs仍然无法直接估算。通过实验观察及前人研究发现，hs主要受到以下几个变量的影响：P，do，Uo，dp，ρp，ρf。以Umf代替dp，ρp和ρf来表示流化气体性质和颗粒性质的影响，仍使用Froude 数作为无因次数，得到以下关联式：

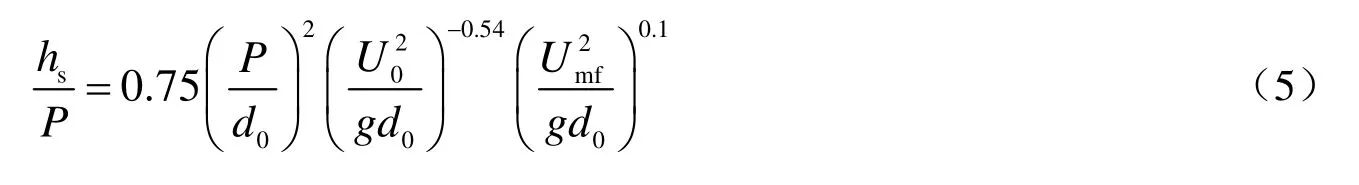
图14为死区高度hs实验值与公式（5）的预测值的比较，可看出大部分实验值在预测值的±40%以内。

3 结 论

对同一种颗粒，射流深度随着孔速的增加而增大；在相同的孔速下，射流深度随孔径的增加而增大，多孔分布板的射流深度更大；对于不同物性的颗粒，在相同的U/Umf下，射流深度基本相同；将U/Umf作为无因次量引进射流深度计算公式，提出了新的射流深度计算公式，对于不同的分布板，预测值都能较好地与实验值吻合。

符号说明

Ao—每个孔对应的分布板面积，m2

do—分布板孔径，m

dm—颗粒运动区直径，m

dp—颗粒直径，m

g—重力加速度，m/s2

hs—颗粒死区高度，m

Lj—射流深度，m

N—分布板孔数

P—分布板孔间距，m

U—表观气速，m/s

Umf—最小流化气速，m/s

Uo—分布板孔速，m/s

Uomf2D—分布板最小流化孔速，m/s

φ—死区颗粒角度，（o）

φr—颗粒休止角，（o）

μ—气体粘度，Pa·s

ρf—气体密度，kg/m3

ρp—颗粒密度，kg/m3

[1]Behie L A, Kehoe P.The grid region in a fluidized bed reactor[J].AIChE Journal, 1973, 19(5):1070-1072.

[2]Rowe P N.A model for chemical reaction in the entry region of a gas fluidised-bed reactor[J].Chemical Engineering Science, 1993,48(14):2519-2524.

[3]Merry J M D.Penetration of vertical jets into fluidized beds[J].AIChE Journal, 1975, 21(3):507-510.

[4]Yang W C, Keairns D L.Estimating the jet penetration depth of multiple vertical grid jets[J].Industrial &Engineering Chemistry Fundamentals, 1979, 18(4):317-320.

[5]Guo Q, Yue G, Yu J, et al.Hydrodynamic characteristics of a two-dimensional jetting fluidized bed with binary mixtures[J].Chemical Engineering Science, 2001, 56(15):4685-4694

[6]Zhong W, Zhang M.Jet penetration depth in a two-dimensional spout–fluid bed[J].Chemical Engineering Science, 2005, 60(2):315-327.

[7]Sauriol P, Cui H, Chaouki J.Gas jet penetration lengths from upward and downward nozzles in dense gas–solid fluidized beds[J].Powder Technology, 2013, 235:42-54.

[8]Wen C Y, Krisshnan R, Dutta S, et al.Dead zone heights near the grid of fluidised beds[C].Fluidisation:Proceeding of 2nd Engineering Foundation Conference, Cambrige University Press, 1978:32-37.

[9]Horio M, Ktyota H, Muchi I.Particle movement on a perforated plate distributor of fluidized bed[J].Journal of Chemical Engineering of Japan, 1980, 13(2):137-142.

[10]Müller C R, Holland D J, Davidson J F, et al.Geometrical and hydrodynamical study of gas jets in packed and fluidized beds using magnetic resonance[J].The Canadian Journal of Chemical Engineering, 2009, 87(4):517-525.

[11]Rees A C, Davison J F, Dennis J S, et al.The nature of the flow just above the perforated plate distributor of a gas-fluidised bed, as imaged using magnetic resonance[J].Chemical Engineering Science, 2006, 61(18):6002-6015.

[12]Agarwal G, Lattimer B, Ekkad S, et al.Influence of multiple gas inlet jets on fluidized bed hydrodynamics using particle image velocimetry and digital image analysis[J].Powder Technology, 2011, 214(1):122-134.

[13]Filla M, Massimilla L, Vaccaro S.Gas jets in fluidized beds and spouts:A comparison of experimental behavior and models[J].The Canadian Journal of Chemical Engineering, 1986, 61(3):370-376.

[14]Meenal P, Holland D J, Chandrasekera T C, et al.Magnetic resonance studies of a gas-solids fluidised bed:Jet-jet and jet-wall interactions[J].Particuology, 2010, 8(6):617-622.

[15]Blake T R, Webb H, Sunderland P.The nondimensionalization of equations describing fluidization with application to the correlation of jet penetration height[J].Chemical Engineering Science, 1990, 45(2):365-371.

[16]Thorpe R B, Davidson J F, Pollit M, et al.Maldistribution in fluidized beds[J].Industrial &Engineering Chemistry Research, 2002, 41(23):5878-5889.