《线性代数》例习题教学研究

成庭荣 (长江大学信息与数学学院，湖北 荆州 434023)

《线性代数》例习题教学研究

成庭荣 (长江大学信息与数学学院，湖北 荆州 434023)

从一题多解、一题多用、一题多变3个方面对《线性代数》例习题教学进行了研究。运用一题多解进行教学，有利于培养学生的发散性思维，这样才能使学生真正具有创新能力和创新精神；综合地进行一题多用的教学，可使学生对所学知识纵向加深，横向沟通，诱导学生对某一问题深入研究，持续思考，整合已学知识，拓展其内蕴，有利于培养学生思维的连续性；通过一题多变的教学，可使学生对所学知识灵活变通，积极思索，激发学生的学习热情，对问题的本质认识、理解得更深刻，有利于培养学生思维的灵活性。

《线性代数》；例习题教学；一题多解；一题多用；一题多变

《线性代数》课本[1]和参考书中，有些例习题具有丰富的内涵，在由知识转化为能力上，具有示范性和启发性，在解题思路和方法上具有典型性和代表性，如果不以得到解答而满足，而是在解完之后，进一步深入地挖掘和多方位的探索，这对于培养学生良好的思维品质是十分有益的[2]。下面，笔者对《线性代数》例习题教学进行了研究。

1 一题多解，培养学生思维的发散性

例1设矩阵A=(a1,a2,a3,a4)，其中a2,a3,a4线性无关，a1=2a2-a3，向量b=a1+a2+a3+a4，求方程Ax=b的通解。

解法1令x=(x1,x2,x3,x4)T是方程Ax=b的解，即x1a1+x2a2+x3a3+x4a4=b，所以：x1(2a2-a3)+x2a2+x3a3+x4a4=a1+a2+a3+a4=2a2-a3+a2+a3+a4

即：

(2x1+x2-3)a2+(-x2+x3)a3+(x4-1)a4=0

因为a2,a3,a4线性无关，从而{2x1+x3=3,-x1+x3=0,x4=1 ,解之得：

解法2因为a1=2a2-a3，则a1,a2,a3线性相关，从而a1,a2,a3,a4线性相关，而a2,a3,a4线性无关，所以R(A)=3，从而方程Ax=0的解集的秩为1，由a1=2a2-a3可知x=(1,-2,1,0)T是Ax=0的解，又因为b=a1+a2+a3+a4所以(1,1,1,1)T是方程Ax=b的一个特解，从而Ax=b的通解为：

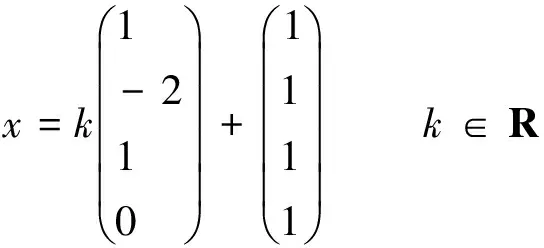
用多种知识和方法处理同一问题，可以引导学生从不同角度，不同方位去思考和处理问题，从而拓宽思路。运用一题多解进行教学，有利于培养学生的发散性思维，这样才能使学生真正具有创新能力和创新精神。

2 一题多用，培养学生思维的连续性

例2设m×n矩阵A的秩R(A)=r，则n元齐次线性方程组Ax=0的解集S的秩RS=n-r。

利用此结论可解决下面的问题：①若n元齐次线性方程组Ax=0与Bx=0同解，则R(A)=R(BB)；②进一步，可得到R(ATA)=R(A)，因为这时只需要证明齐次线性方程组ATAx=0与Ax=0同解即可；③再进一步可得到矩阵A=O的充分必要条件ATA=O

综合地进行一题多用的教学，可使学生对所学知识纵向加深，横向沟通，诱导学生对某一问题深入研究，持续思考，整合已学知识，拓展其内蕴，有利于培养学生思维的连续性。

3 一题多变，培养学生思维的灵活性

例3设n阶行列式D=det(aij)，把D上下翻转，得到：

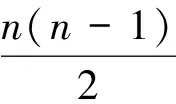
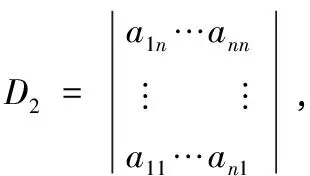
通过一题多变的教学，可使学生对所学知识灵活变通，积极思索，激发学生的学习热情，对问题的本质认识、理解得更深刻，有利于培养学生思维的灵活性[3]。

4 结 语

例习题教学的多样化，可唤起学生的求知欲望，激发学生探究知识的兴趣，使学生掌握“由已知到求知，从现象到本质”的认识世界的根本方法，使之思维方式多元化，从而达到提高解决实际问题的能力。

[1]同济大学教学系. 线性代数[M].北京：高等教育出版社，2007.

[2] 王秀珍. 《线性代数》习题课教学与改革的初步探讨[J]. 课程教育研究(新教师教学)，2012(16)：136.

[3] 高梅. 浅谈《线性代数》习题课的教与学[J]. 科技信息2010(2)：134.

2013-07-23

成庭荣(1962-),男，副教授，现主要从事基础数学方面的教学与研究工作。

N4

A

1673-1409(2013)28-0135-02

[编辑] 洪云飞