关于合肥市“出租车拼车”问题的优化研究*

刘书曼，周宗福，张 晨，黄跃辉，陈诗扬

(安徽大学数学科学学院，合肥230601)

出租车作为城市交通系统的一员，它需要为城市交通系统运输效率的提高做出贡献。但目前出租车“兜客式”的经营方式造成了“空车”和低实载率的现象，反而降低了道路运输效率，同时也增加了城市的环境污染。“拼出租车”的兴起有利于减轻交通负担，同时还节约了资源，减少了尾气污染，而且对于乘客而言，降低了出行的成本。

“拼出租车”即指具有大体相同行驶方向和路径的乘客，共同乘坐一辆出租车［1］。国内对“拼出租车”问题已做过一些研究，文献［2］［3］对于拼车路线优化以及费用分摊问题给出了解决方案，但在考虑路线优化时只是将最短路程作为最优目标，没有考虑交通状况的拥挤以及其他的时间成本。此处则综合考虑影响最优路线的因素:路程、交通状况、人的满意度等。对于费用分摊，研究也不同于文献［2］，不仅将路程作为费用分摊的唯一依据，还考虑了乘客的优先级指数，充分体现了公平性原则。

1 研究的前期准备

主要通过进行一定范围的问卷调查来了解合肥市内的“拼出租车”情况，共发出问卷500张，实际有效问卷380张。通过统计问卷调查数据发现:

在拼车的能愿度上，大多数人倾向于拼车出行，其中愿意与别人拼车的占63.3%，不愿意与别人拼车的占36.7%，这为此问题的研究提供了动力，也说明此项研究具有研究的实际意义。在拼车目的性上，认为以快速到达目的地为优先的占54.55%，认为以节约金钱为优先的占45.45%，这样，在建立层次分析模型时，可以设定时间和费用的量化比值为6∶5。在拼车管理上，有87.88%的人认为需要在合肥市制定出相应的一套“拼出租车”管理措施(在问卷调查过程中，也了解到有些出租车司机强行拼车，对每位乘客收取不变的费用，这显然是不公平的，这也是研究费用分摊问题的原因)。在拼车费用的收取上在问卷中给出了按路程和按人数两种方案，赞成按人数定折扣合适的比例以及赞成按路程的远近定费用合适的比例见图1、图2。

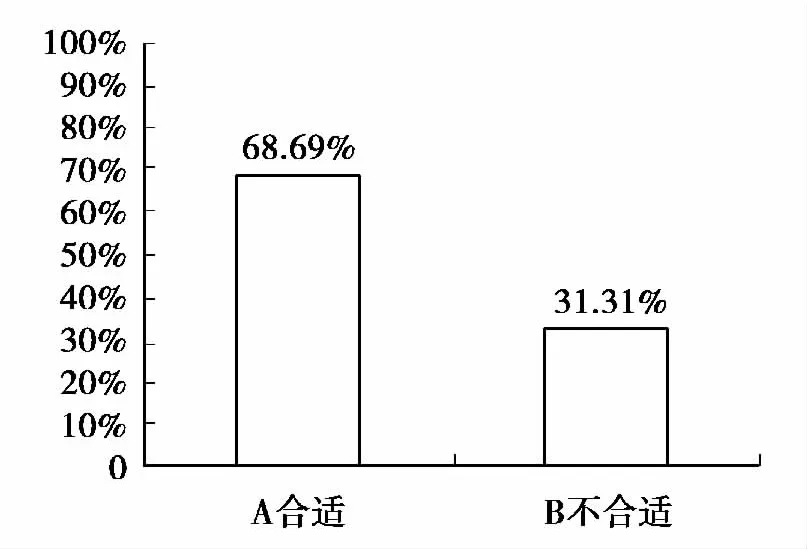
图1 按人数定折扣

图2 按路程远近定费用

2 拼车最优路线问题的研究

2.1 问题的描述

研究的情况是合肥市内存在一定潜在数量的乘客群，由于某种目的而引发“拼出租车”需求，并且了解到合肥市内存在的拼车模式更多的是“一对多”模式，即只将相同的起点但是不同终点的乘客进行配对运送，其拼车模式如图3。此处研究的就是在类似情形下的拼车路线优化问题和拼车费用分摊问题。

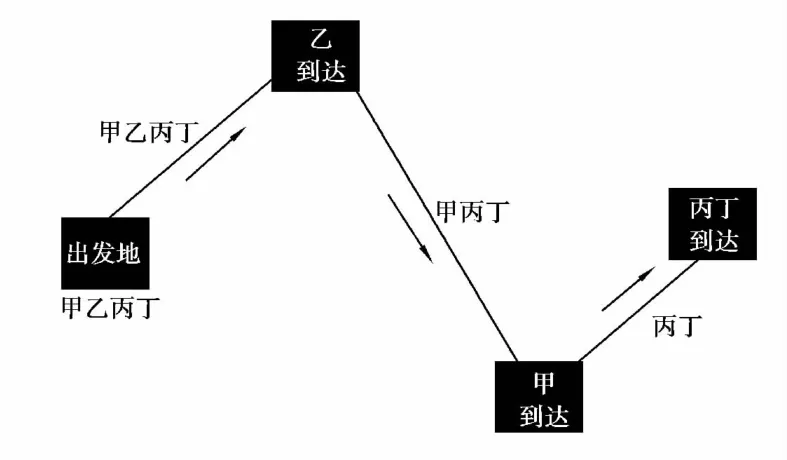
图3 “一对多”拼车模式

图4 合肥市部分路线图

2.2 拼车路线最优化数学模型的建立与分析

2.2.1 选择合适的合乘乘客

在解决“拼出租车”所引发的相关问题之前，首要解决的问题是选择合适的合乘乘客，例如在合肥市某个站口，有数量较多的乘客有需求“拼出租车”(假设这些乘客群已自动分好组，即去往同一个方向的在一组)，且同在一组的乘客数超过了出租车的最大载客量，此时就要考虑选择合适的乘客人群。在这里，引入乘客优先级的量化系数μ，用来描述拼车对象的选取以及乘客到达各自目的地的先后顺序。

如何确定合理的μ值是关键的一步，考虑到出租车出发点到目的地的距离，乘客的紧急程度，以及对合乘者的性别要求等因素与μ有很大关系，因此利用这些因素来确定μ值，故引入距离因子κ，乘客的紧急系数 υ(υ∈(0，1))，乘客提出的特殊要求度 ξ(ξ∈(0，1))，这样，可以建立模型计算 μ 值:

其中，x1，x2，x3∈(0，1)为 κ，υ，ξ之间的权重比值，通过统计分析可以确定的 x1，x2，x3的值分别为 x1=0.713，x2=0.207，x3=0.080，κ，υ，ξ各值依实际情况而定。综合考虑乘客的情况进行定量计算，就可以得到的乘客优先级的量化系数μ值，以此作为选择合适乘客的决策标准，μ值越大，选择为合乘对象的可能性就越大。

2.2.2 模型的建立与分析

(1)路线简化图的建立。考虑的最优线路是指:路程最短，交通状况最优，红绿灯个数最少，路程最短即指所花的费用最省，时间最少，交通状况与红绿灯个数也与时间相关。考虑到拥挤的交通状况会使乘客焦虑，降低人的幸福感，故另外引入满意度系数λ∈(0，1)，λ可根据交通状况拥挤程度(车流量来衡量)确定。为了简化研究的复杂性，选取部分路线进行研究。假定有5位乘客需要拼车，如图4(其中选取了5个目的地和一个出租车出发点，用表示)。

其中，主要的道路为黄山路、金寨路、屯溪路、徽州大道、马鞍山路、巢湖路、芜湖路、明光路。

利用图论相关知识，将选取的地点抽象为顶点(节点)，将地点之间的路线抽象为边(链接)，给出了合肥市部分路线简化图，如图5。

图5 合肥市部分路线简化图

其中，V= { v1，v2，…，v13}为该路线简化图的顶点集，E= {e1，e2，…，e17}为该路线简化图的边集。v1代表出租车出发点，顶点 v4，v7，v8，v12，v11分别代表目的地 1，2，3，4，5，乘客 i到达目的地 i。根据实际情况及假定的乘客需求分析，通过式(1)给出表1。

表1 乘客优先级量化系数表

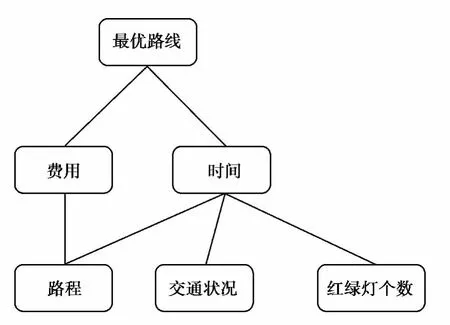
图6 关于路线优化的层次分析图

因此，根据乘客优先级的量化系数μ值得大小，选择本次合乘乘客是乘客1、乘客2、乘客3和乘客4。

(2)路线简化图边权重的确定。接下来需要确定每条边的权重，构造赋权路线图模型。先通过建立模糊层次分析［4］模型来确定各个因素对最优路线的贡献比例，再进一步确定各边的权重。

模糊层次分析法引入模糊一致矩阵［5］，无需再进行一致性检验，同时使用幂法来计算权向量，可以得到计算精度较高的且与实际情况较吻合的权向量。以下是具体步骤:

1)确定目标层为最优路线，指标层为费用和时间，因素集为路程、交通状况、红绿灯的个数。图6表示之间的层次关系。

2)利用0.1 ～0.9 数量标度［5］，构造优先关系矩阵 F=(fij)n×n。

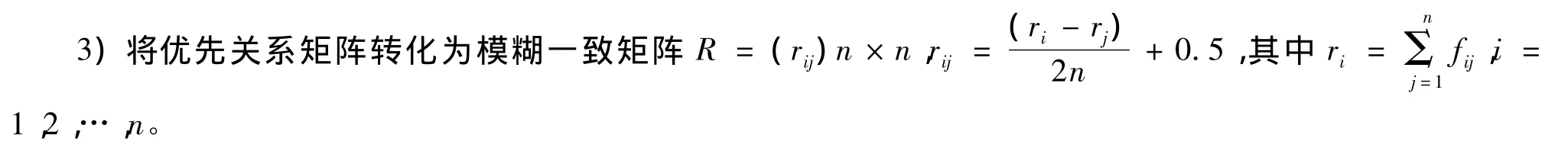
4)利用幂法［6，7］计算权向量 W。

其中，ω0代表初边权重，式(2)中的路程代表的并非实际具体数据，而是各边之间的比例关系(以最短路程作为基准，分别与其他各边进行比值)，交通状况指数则是根据车流量的大小，赋予1～9这些数值得到的。红绿灯指数则是各地点之间的红绿灯个数比值。

由前面所述，此处还引入了满意度系数λ，表示乘客对交通状况的心里感受，因此在计算最终边权值时将λ设为最终的影响边权重的因子，建立如下模型计算ω:

得到图3中每条边的权重如表2:

表2 路线简化图的各边权重

(3)基于分步Floyd算法的最优路线方案。研究的两点之间的最优路线是指在图5中找两点之间权值和最小的那些边，采用的是Floyd算法［8］求解两点之间的最小权值路线。虽然Floyd算法是用来求解两点之间最短路径的算法，此处将最短路径扩展为最小权和路线，考虑了多种因素对最优路线的影响，这也是合理的。

在之前，已经确定了乘客的优先级，即确定了出租车送往目的地的顺序，因此，想利用分步的Floyd算法找到最优路线，即首先利用Floyd算法找到顶点v1到v4的最优路线，然后再利用同样的方法找顶点v4到v7的最优路线，依次类推，直到找到顶点v8到v12的最优路线，其中分步计算的想法是类似于图论学科中找最短路径的常用的最邻近算法［9］。寻找最优路线具体过程:

1)顶点v1到v4的最优路线:考虑的顶点是v1，…，v5。

① 构造权重矩阵 D1(wij)5×5，其中当(vi，vj)∈E 时，wij就为顶点 vi到 vj的边权值，若(vi，vj)∉E，wij=∞，即:

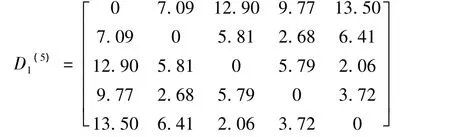
③最后，通过反向追踪法确定顶点v1到v4的最优路线，即是:

2)通过同样的方法，依次得到顶点v4到v7，顶点v7到v8，顶点v8到v12的最优路线为:

3 基于最优路线的拼车费用分摊问题的解决方法

3.1 拼车费用分摊问题的分析

对于拼车费用的分摊，主要从公平性原则出发。通过调查了解到有的地区拼车费用采用固定的费率分摊，如按人数定折扣或按路程定折扣，这虽然具有一定的合理性，但还有一些关键因素没有考虑在内，例如在最优路线选取的问题上考虑了乘客的优先级，对于那些优先级高的乘客有必要多收取一些费用(假定每位乘客都是理性人，地位是对等的，若有某位乘客因为自己特殊要求以及时间紧急对其他乘客产生消极的外部性，他需要对自己产生的消极外部性多支付一些费用)。结合前期的调查准备，综合考虑按人数定折扣和路程远近两种方式解决费用分摊问题，由于按人数定折扣方案在费用分摊计算中是隐形体现的，因为拼车人数越多(最大不超过出租车最大载客量)，分摊的费用越少，形象上说是折扣越多，因此在计算费用分摊时只考虑路程远近以及乘客的优先级指数δ，用来表示各乘客的紧急系数υ与特殊要求度ξ之和的比值。

3.2 费率ri的确定

先引入一些参数，C为总费用，C0为出租车起步价，L0为起步价路程，r0为正常费率(即超过起步价路程后每公里价格)，Ci为第i位乘客所需支付的费用，li(i=1，2，…，n)为分段的路程，即l1表示出租车出发点到目的地1的路程，l2表示目的地1到目的地2的路程，以此类推。

拼车费用的分摊即如何将C分割，使每位乘客所支付的费用Ci尽可能是公平的。此问题的关键是找到恰当的比例ri(表示第i位乘客的费率)，使得Ci=ri×C，C=C1+…+Cn(可能存在乘客到达目的地的路程小于L0，则该乘客需支付的费用为C0/n，n为拼车总人数)。此处所考虑的ri与路程远近和乘客的优先级指数δ有关。

前文，在确定乘客优先级的量化系数μ时，考虑了距离因子κ，乘客的紧急系数υ，乘客提出的特殊要求度ξ，并给出了3者的权重比值，则以此为依据考虑路程远近和乘客优先级之间的权重比，设定I1，I2，其中I1表示路程远近对ri的贡献度，I2表示乘客优先级指数δ对ri的贡献度，则建立如下模型计算ri:

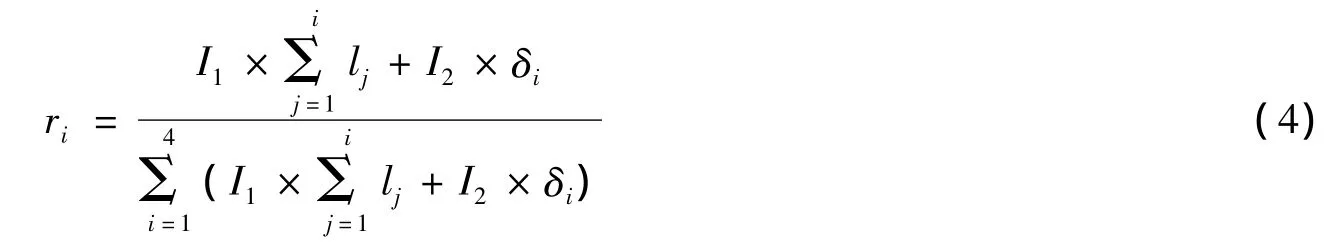
其中，δi表示第i为乘客的优先级指数，可以利用给出的υ与ω的值，通过数学上常用的取比例值的方法得到(针对不同的拼车情况，δi的取值是不同的)，公式(1)中lj可以不是具体的路程数据，只要确定比例关系即可。

结合实际研究的问题，n取4，则 C=C0+r0×(l1+… +l4)。并设定 I1=0.713，I2=0.287，通过计算，最终得到:r1=0.13，r2=0.20，r3=0.30，r4=0.37，于是每位乘客所需支付的费用为

按照这样的比例分摊费用无疑充分地体现了公平。

4 结语

“拼车问题”是当今人们比较关心的一个问题，由于没有相关运营方法规定，在路线与费用收取上处于比较混乱的状态。通过建立数学模型，提出了路线最优化与费用分摊的解决方案，具有一定的实际意义，希望在对相关策略的制定中会有所帮助，对于该问题的进一步研究提供参考。

［1］王罗.出租车共乘问题研究［D］.长沙:长沙理工大学，2008

［2］覃运梅，石琴.出租车合成模式的探讨［J］.合肥工业大学大学学报:自然科学版，2006，29(1):77-79

［3］郭瑞军，王晚香.基于矩阵迭代法的出租车合乘最短路径选择［J］.大连交通大学学报，2011，26(1):29-32

［4］张吉军.模糊层次分析法(FAHP)［J］.模糊系统与数学，2000，14(2):86

［5］张燕姑.基于模糊一致矩阵的研究［J］.计算机工程与设计，2005，26(6):1492-1493

［6］徐萃薇，孙绳武.计算方法引论［M］.北京:高等教育出版社，2007

［7］周铁，徐树方，张平文，等.计算方法［M］.北京:清华大学出版社，2006

［8］胡运权，郭耀煌.运筹学教程［M］.北京:清华大学出版社，1998

［9］SOLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constrains［J］.Operations Research，1987，35(2):254-265