解无约束优化的非单调自适应信赖域算法

曾刘拴

(重庆大学 数学与统计学院，重庆401331)

0 引言

本文考虑无约束最优化问题:

其中，f(x):Rn→R二阶连续可微且有下界。信赖域方法是一种迭代方法，在每次迭代中，试探步dk可通过求解下面的子问题得到:

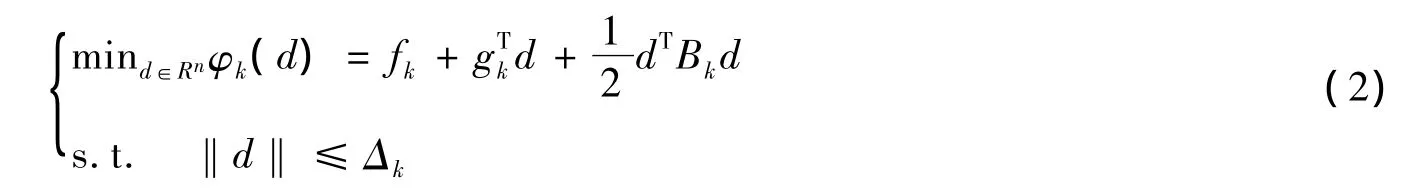
其中 d=xk+1－xk，gk=∇f(xk)，对称阵 Bk∈Rn×n是∇2f(xk)或其近似，Δk＞0 是信赖域半径，‖.‖是向量范数或由它导出的矩阵范数。由式(2)求得的试探步d是否被接受，取决于两个下降量的比值，即，其k中Aredk=f(xk)－f(xk+dk)表示实际下降量，Predk=φk(0)－φk(dk)表示预测下降量。

无约束信赖域方法的收敛结果是由Powell［1］首次得到的，后经许多学者的研究，信赖域方法得到了很好地发展，已经成为优化算法两大分支之一。2000年，Conn等人出版了关于信赖域方法的专著［2］。近年来，非单调线搜索技术得到广泛应用，此方法是Grippo等［3］首次提出的，因其具有较好的数值效果而得到了广泛应用。关于非单调技术的研究主要有文献［4-6］等。2008年，Mo和Gu［7］提出了一种较为简单的非单调技术，即:

并将此技术运用到信赖域方法中，获得了较好的数值效果。

自适应方法是由Sartenear［8］首次提出的，此方法可以避免信赖域半径更新的盲目性。自适应方法进一步研究的主要有文献［9-10］等。2009年，Sang和Sun［11］充分利用当前迭代点的信息提出了一种自适应方法，即令:

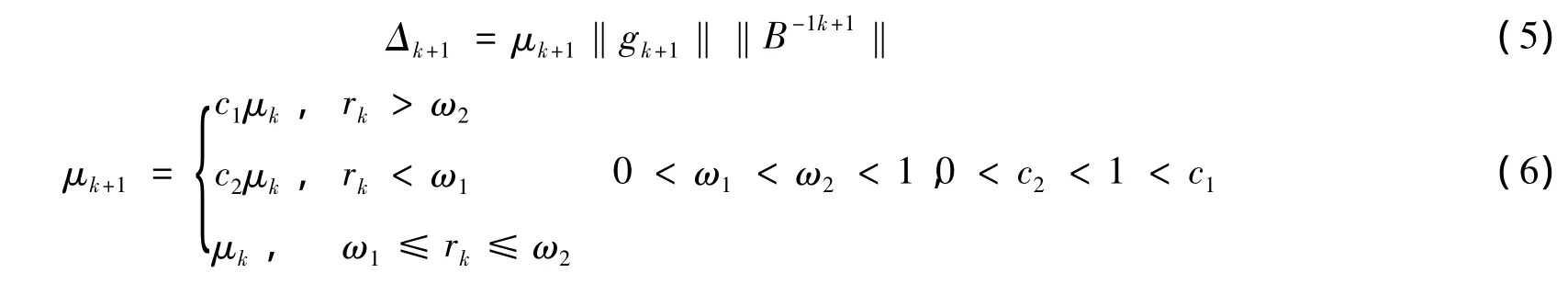
滤子技术是由Fletcher和Leyffer［12］提出的，其最初的目的是为了克服使用价值函数时选取罚因子的困难。2005年，Gould等［13］将滤子技术应用到一般的无约束优化问题中，提出了一个滤子信赖域方法，证明了其收敛性，并得到较理想的数值效果。

本文基于简单二次模型式(2)，结合 Mo等［7］的非单调技术、Sang和 Sun［11］的自适应技术及 Gould等［13］的滤子技术提出一个非单调自适应信赖域算法。当试探步不被接受时，采用滤子技术，增加试探步被接受的可能性;如果试探步也不被滤子集接受，取dk=－，沿dk方向进行非单调Armijo线搜索，得到步长αk，从而得新的迭代点 xk+1=xk+αkdk。

1 基于二次模型的非单调滤子自适应信赖域算法

1.1 算法1(FNTR)

步1:给定 x0∈Rn，0 ＜ ω1＜ ω2＜1，μ0=1，δ∈(0，0.5)，η∈(0，1)，λ∈(0，1)，ε ＞0。0 ＜ c2＜1 ＜ c1，0 ＜ c2＜1＜＞0，γg∈=E(单位阵)，初始滤子集 F0，k←0。

步 2:计算‖gk‖，若‖gk‖≤ε，则 x*=xk，停止计算，否则，转步 3。

步3:计算f(xk)，Bk解信赖域子问题得试探步dk，令=xk+dk。

步5:若rk≥ω1，令xk+1=;否则，计算=g()，若被Fk接受，令xk+1=，并将加入到Fk，同时去除Fk中所有被支配的点，得到Fk+1;否则，令dk=－，求ik，使得ik是满足

的最小的非负整数，令 αk=λik，xk+1=xk+αkdk。

步6:按式(5)、式(6)更新信赖域半径，转第2步。

说明:∀i=1，2，…，n，算法1第3步中的实正定对角矩阵:

1.2 算法的收敛性

在此给出以下假设:(M)f(x)在有界闭集H={x|f(x)≤f(x0)}上二阶连续可微。为讨论问题的方便，记 T={k|rk≥ω1}，S={k|加到滤子集中}，A={k|rk＜ω1}/S。

引理1［14］如果{B}是由算法1产生的，则对任意的k，Bk及都是正定对角阵，L≤‖B‖≤L，且存在 m1，m2＞0 使得 m1≤‖‖≤m2。

引理2［11］若dk是子问题(2)的解，则有:

即有Dk+1≤Dk，所以当k∈T时结论成立。

第二种情况:k∈S

由滤子的定义知 fk+1≤fk。若 k －1∈T，则有 fk≤Dk≤Dk－1，从而有 Dk+1= ηDk+(1 － η)fk+1≤ηDk－1+(1 －η)fk=Dk，即 Dk+1≤Dk，又因 Dk+1－ fk+1=η(Dk－ fk+1)≥η(fk－ fk+1)≥0，即 fk+1≤Dk+1，所以有 fk+1≤Dk+1≤Dk。若 k －1∈S，令 M={i|1 ＜ i≤k，k －i∈T}。如果 M=Φ，则有 fk+1≤fk≤…≤f1≤f0=D0。

下面用数学归纳法证明Dk+1≤Dk。

因 D0=f0，所以 k=1 时有 D1=ηD0+(1 －η)f1≤ηf0+(1 － η)f0=f0=D0。假设 k=n时，有 Dn+1≤Dn，下证 k=n+1 时有 Dn+2≤Dn+1。而 Dn+2=ηDn+1+(1 － η)fn+2≤ηDn+(1 － η)fn+1=Dn+1。所以 Dk+1≤Dk成立;再证 fk+1≤Dk+1，因 Dk+1－Dk=(η－1)Dk+(1－η)fk+1=(1－η)(fk+1－Dk)。

而由上面的证明可知 Dk+1≤Dk，又1 － η ＞0，所以有 fk+1－Dk≤0，即 fk+1≤Dk，从而有 Dk+1=ηDk+(1 －η)fk+1≥ηfk+1+(1 － η)fk+1=fk+1。如果 M≠Φ，设 m=min{i|i∈M}，则有 fk+1≤fk≤…≤fk－m+1，因 k－ m∈T，由第一种情况可知 fk－m+1≤Dk－m+1≤Dk－m，而 Dk－m+2= ηDk－m+1+(1 － η)fk－m+2≤ηDk－m+(1 － η)fk－m+1=Dk－m+1。由归纳法可得 Dk+1≤Dk，从而同上可得 fk+1≤Dk+1。

综上可得当 k∈S 时，有 fk+1≤Dk+1≤Dk。

第三种情况:k∈A

则有 Dk+1＜ Dk，所以有 fk+1≤Dk+1≤Dk。

综合上面三种情况可知，对任意的k都有fk+1≤Dk+1≤Dk。

引理5［7］如果假设(M)成立，αk满足式(7)，则对任意的k∈A都有:

反证，假设对充分大的k有‖gk‖≥ε0＞0。

证明:反证，假设当k充分大时，有‖gk‖≥ε＞0。

由引理4知{Dk}单调下降，又{Dk}有界，故其收敛，再由引理3和引理5得:

2 数值试验

本节给出算法1(FNTR)的数值试验结果，并与基本信赖域算法(TR)(文献［15］中算法3.6.1)做比较。算法用Matlab 7.01编写程序。Fval表示最优点处的函数值，Gnorm表示迭代终止时函数梯度的范数，K表示迭代次数，CPU代表运行时间(单位为s)。设定精度‖gk‖≤10－3。检验函数取自文献［16］，初始点的选取与文献［16］相同。如果计算不出结果或者时间超过200 s或者迭代次数超过1 000次，则用“—”表示。

算法1(FNTR)中，选择的参数:μ0=1，ω1=0.20，ω2=0.80，c1=1.5，c2=0.5，λ =0.5，δ=0.4，η =0.15，γg=min{0.003。检验函数如表1，数值结果如表3。其中各个函数中和的选取见表2。

表1 检验函数对应编号

表2 和的值

表2 和的值

?

3 结束语

从表3的数据可以看出，对绝大多数测试函数，算法1(FNTR)具有迭代次数较少、运行时间较短的优势，且对于测试函数中的rosex，singx，pen1，vardim，bv这些函数，在高维情况下基本信赖域算法失效，而算法1(FNTR)则可以很好地求解，因此算法1(FNTR)是比较有效的，而对于trig，ie这两个函数算法1(FNTR)的优势不太明显，有待进一步研究。

表3 算法1(FNTR)和基本信赖域算法的数值结果

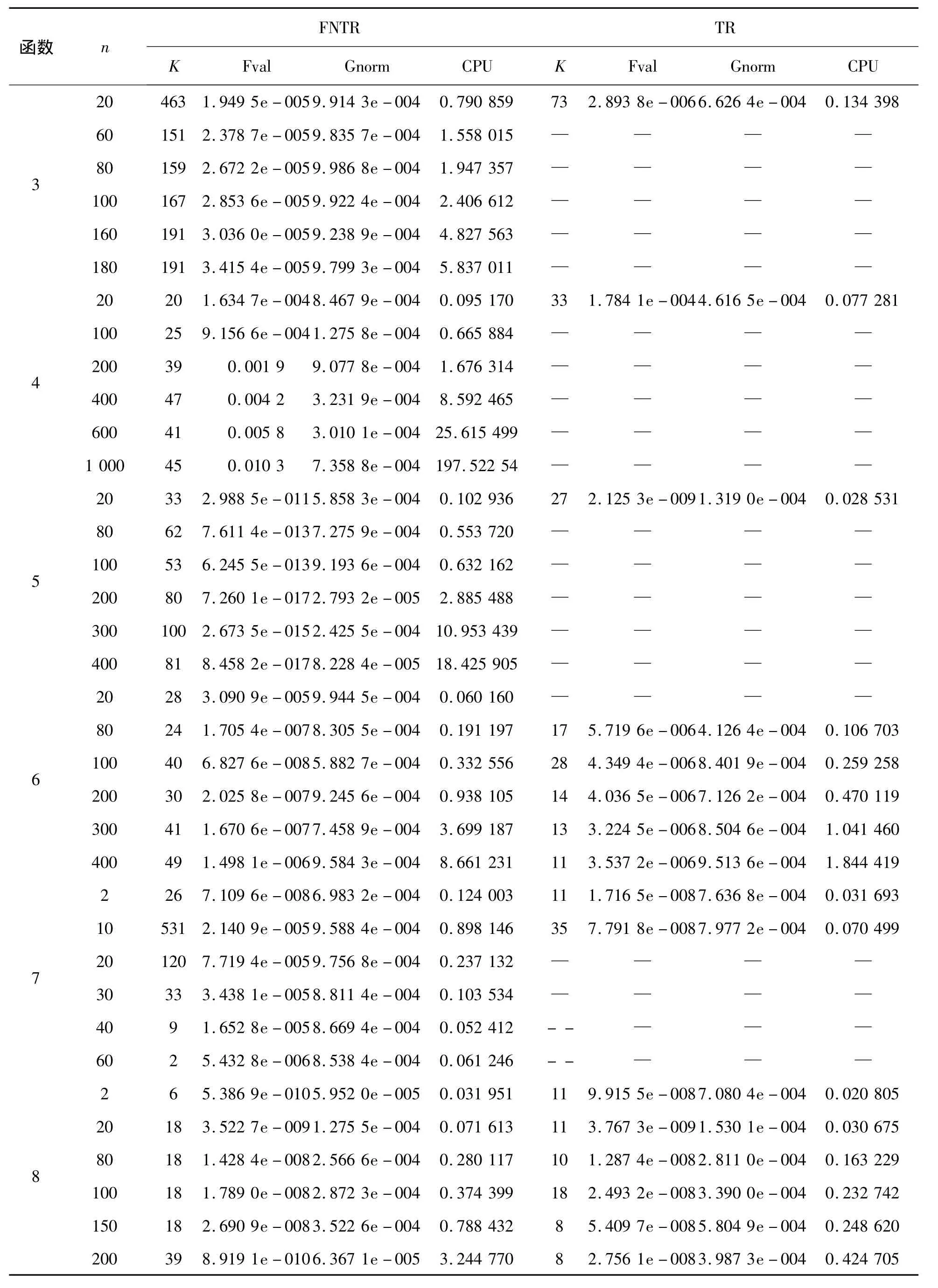
续表

［1］ POWELL M J D.Convergence properties of a class of minimization algorithm［C］//Nonlinear Programming II，New York，Academic Press，1975:1-27

［2］CONN A R，GOULD N I M，TOINT Ph L.Trust－ Region Methods［M］.SIAM Publications，2000

［3］GRIPPO L，LAMPARIELLO F，LUCIDI S.A nonmonotone line search technique for Newton’s method［J］.SIAM Journal on Numerical Analysis，1986，23(4):707-716

［4］DENG N，XIAO，ZHOU F J.Nonmonotone trust region algorithm［J］.Journal of Optimization Theory and Applications，1993，76(2):259-285

［5］ZHANG H，HAGER W.A nonmonotone line search technique and its application to unconstrained optimization［J］.SIAM Journal on Optimization，2004，14(4):1043-1056

［6］MO J，LIU C，YAN S.A nonmonotone trust region method based on nonincreasing technique of weighted average of the successive function values［J］.Journal of Computational and Applied Mathematics，2007，209(1):97-108

［7］GU Z，MO J.Incorporating nonmonotone strategies into the trust region method for unconstrained optimization［J］.Computers and Mathematics withApplications，2008，55(9):2158-2172

［8］SARTENAER A.Automatic determination of an initial trust-region in nonlinear programming［J］.SIAM Journal on Scientific Computing，1997，18(6):1788-1803

［9］FAN J，YUAN Y.A new trust region algorithm with trustregion radius converging to zero［C］//Proceedings of the 5th International Conference on Optimization:Techniquesand Applications，HongKong，Dec，2001

［10］ZHANG X，ZHANG J，LIAO L.An adaptive trust method and its convergence ［J］.Computers and Mathematics with Applications，2003，45(10-11):1469-1477

［11］SANG Z，SUN Q.A self-adaptive trust region method with line search based on a simple subproblem model［J］.Journal of Computational and Applied Mathematics，2009，232(2):514-522

［12］FLETCHER R，LEYFFER S.Nonlinear programming without a penalty function［J］.Mathematical Programming，2002，91(2):239-269

［13］GOULDN I，SAINVITUC，TOINTP.A filter-trust-region method for constrained optimization［J］.SIAM Journal on Optimization，2005，16(2):341-357

［14］冯琳，段复建，和文龙.基于简单二次函数模型的滤子非单调信赖域方法［J］.山东大学学报:理学版，2012(5):1-8

［15］袁亚湘，孙文瑜.最优化理论与方法［M］.北京:科学出版社，1997

［16］MORE J，GARBOW B，HILLSTROM K.Testing uncontrained optimization software［J］.ACM Trans Math Softw，1981，7(1):136-140.