基于改进单纯形法的零件几何误差评定

黄 祥

基于改进单纯形法的零件几何误差评定

黄 祥

（安徽国防科技职业学院实训中心，安徽，六安 237011）

在建立几何误差评定规划模型的基础上，以轴类零件圆度的评定为例，应用改进单纯形法对几何误差规划模型进行优化求解，并给出了详细的求解进程。将评定结果与现有的优化算法结果进行了对比，结果表明基于改进单纯形法的几何误差评定，具有精度高和计算速度快的优点，在实际生产中有较好的实用性。

几何误差；改进单纯形法；误差评定；规划模型

0 引言

在现代工业生产中，不但要求零件保证其尺寸精度，对它的形状和位置精度也有很高的要求。准确地评定零件的几何误差，为提高零件加工精度和装配精度提供可靠的依据。随着近代科学的迅速发展和生产水平的不断提高，零件的制造精度和检验仪器的计量精度也随之有了较大的提高，因而对几何误差的评定方法、评定理论、解算方法等问题的研究，便成为计量学领域研究的热点。

零件几何误差的优化评定是一件比较复杂的工作，目前评定大多数采用最小二乘法，该评定方法计算简单快捷，但仅能近似评定，不能满足几何误差最小条件评定原则[1]。严格的按照最小条件进行评定的方法是最小区域法[2]，其本质在于按不同的准则求出相应的理想要素，在数学上属于极大值极小化问题或极小值极大化问题[3]。在建立典型几何误差评定规划模型的基础上，探讨将改进单纯形法应用于几何误差的优化评定中，以求对形状误差的评定能够在精度与速度上有所突破，实验结果表明该方法结果精确、运算速度快，且在计算机上实现智能判定和结果可视化。

2 典型几何误差规划模型的建立

几何误差是实际要素对其理想要素的变动量，理想要素的位置是决定误差大小的重要因素。依据理想要素的位置和几何误差之间的关系，通过误差变换，建立典型几何误差优化评定模型如下。

①平面度评定模型

式中为目标函数，和为特征参量，分别表示理想外接圆最大半径和理想内接圆最小半径。

②圆度误差评定模型

用两个理想同心圆包容实际要素为最小时，包容域的宽度即为圆度误差，为双包容拟合，圆度最小区域评定规划模型为：

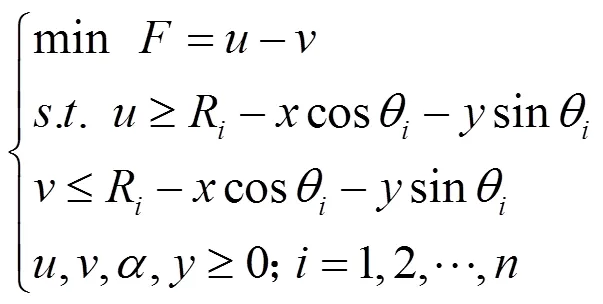
被测点以 (θ,R)来表示，其中θ为转角参数， R为采样点处测得的半径值。

③圆柱度误差评定模型

用两个同轴的理想圆柱包容实际要素，当包容域最小时，包容域宽度即为圆柱度误差，为双包容拟合，圆柱度最小区域评定规划模型为：

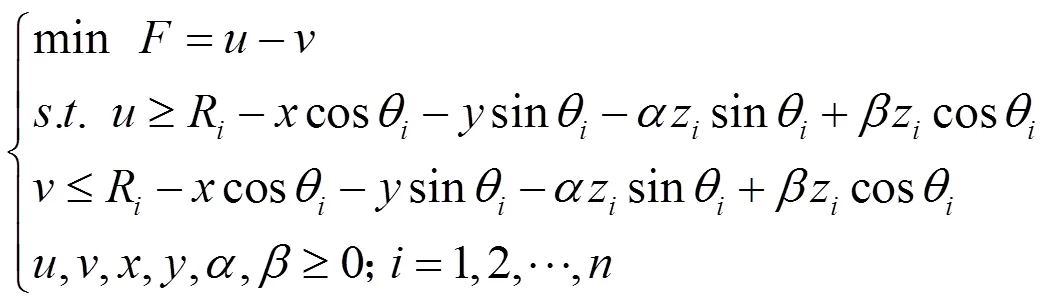
被测点以 (θ,z,R)来表示，其中θ为转角参数，z为轴向坐标，R为采样点处测得的半径值。

④平行度（面对面）评定模型

用两个与基准平面平行的平面，去包容实际要素（平面），当包容为最小时达到定向最小，包容域宽度即为平行度误差。平行度最小区域规划模型为：

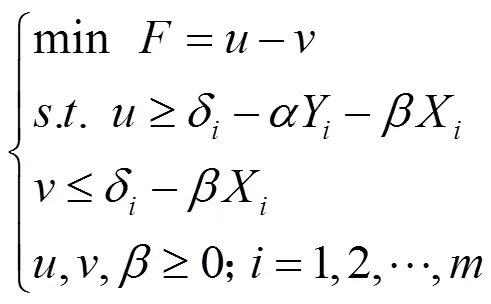
上述仅讨论了常见典型几何误差的评定模型，实际上，通过研究理想要素的位置和几何误差之间的关系即误差变换，诸多几何误差评定问题都可以归结为形如以上的线性规划问题，其实质是一个目标约束优化的过程。

2 规划模型的改进单纯形法求解

误差评定规划模型求解实际上是复杂线性规划的求解。标准线性规划的可行域是凸多面体，若非空，则必有基本可行解；若有最优解，则必有最优基本可行解。由此看来，只须进行基本可行解的叠代。单纯形法的寻优过程可以通过基本可行解来描述：①把线性规划问题的约束方程组表达成典范型方程组，找出基本可行解作为初始基本可行解。②若基本可行解不存在，即约束条件有矛盾，则问题无解。③若基本可行解存在，从初始基本可行解作为起点，根据最优性条件和可行性条件，引入非基变量取代某一基变量，找出目标函数值更优的另一基本可行解。④按步骤③进行迭代，到对应检验数满足最优性条件，即得到问题的最优解。

对于典范型线性规划模型表示为[4]：

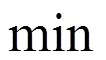
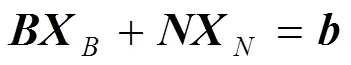
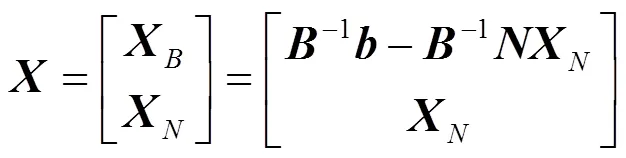
与其相应的目标函数值是

1）将把一般线性规划问题化为典范型；

3 实例分析

图1为一阶梯轴[5]，现要对零件某段进行圆度误差评定，其圆度公差值为t=0.008mm，采用六截面等间距周线测量法进行数据的提取，利用改进单纯形法评定某截面处圆度误差，并与其它评定方法进行比较。

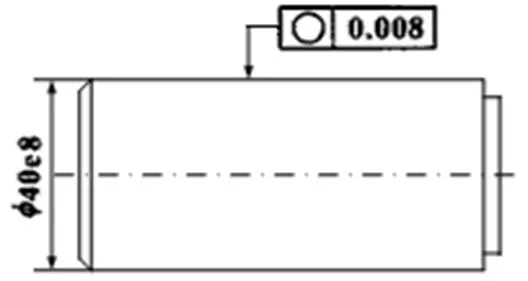
图1 被测轴

表1为改进单纯形法、最小二乘法、最小外接圆法、最大内切圆法圆度评定结果，规划模型求解方法采用改进单纯形优化算法，由表中数据可见，改进单纯形法评定结果最小，可以用来对零件圆度合格性进行仲裁。

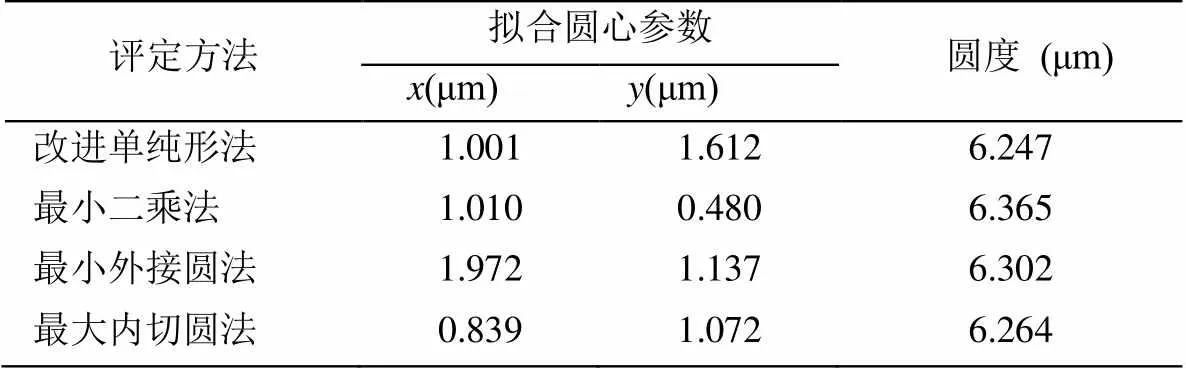
表1 圆度评定结果单位(μm)

4 结论

依据几何误差特征建立了典型几何误差评定数学模型，并将规划模型归为线性规划问题。提出了将改进单纯形法应用于几何误差模型的优化求解中，通过计算机模拟和实测，验证了几何误差评定的正确性、可行性和较好的实用性,这为实际工程中几何误差的快速而准确的评定提供理论基础和技术支持。

[1] ISO/TS 17450-1:2000(E) Geometrical Product Specification (GPS) —General concepts—Part 2:Model for geometrical specification and verification [S].

[2] 李秀明,石照耀.基于凸多边形的直线度误差的评定[J]. 机械科学与技术, 2008,27 (6):736-738.

[3] 郑鹏,张琳娜. 形状误差目标函数单谷性的分析与研究[J].计量与测试技术, 2007, 34(11):16-18.

[4] 粟时平,李圣怡,王贵林.基于鞍点规划法的形位误差计算机评定[J].计量学报,2003,24(1):26-28.

PART GEOMETRIC ERROR EVALUATION BASED ON MODIFIED SIMPLEX METHOD

HUANG Xiang

( Centre of Training Anhui Vocational, College of Defence Technology Liuan, Liuan, Anhu 237011, China)

We proposed the modified simplex method on solving optimization programming model of geometric errors based on the establishment of geometric error evaluation planning model. We also present a detailed solving process. The assessment results are compared with the results of existing optimization algorithm. The results show that the geometric error evaluation based on the modified simplex method has the advantages of high accuracy and fast calculation speed, which has the good practicality in actual production.

geometric error; modified simplex method; error verification; programming model

TH124; TG801

A

10.3969/j.issn.1674-8085.2013.03.015

1674-8085(2013)03-0063-03

2012-05-15；

2013-03-06

2013年度安徽省高等学校省级自然科学研究项目(KJ2013B047)

黄 祥(1969-)，男，安徽六安人，副教授，硕士，主要从事数控技术与测控技术方面研究(E-mail:ahhx6902@163.com).