多维随机变量函数变量变换法的推广

王凡彬

多维随机变量函数变量变换法的推广

王凡彬1,2

（1. 内江师范学院数学与信息科学学院，四川，内江 641110；2. 四川省高等学校数值仿真重点实验室，四川，内江 641110）

对现行的多维随机变量函数的变量变换法进行了讨论，克服了其要求存在唯一反函数的缺陷。应用密度函数的相关性质等方法，把目前的变量变换法推广到了多值函数的情形，可利用多值函数的一支进行变量变换。扩大了现行变量变换法的应用范围。最后给出了应用。

多维随机变量；变量变换法；多值函数；推广

在求多维随机变量的函数问题中，有多种情形和多种方法。而在维随机变量到维随机变量的变换过程中，变量变换法是一个重要的工具。为方便起见，下面主要以二维连续随机变量到二维连续随机变量的变换为例，探讨函数的密度，更高维情形的讨论是类似的。在现行的教材[1]中，一般是这样对变量变换法进行介绍的：

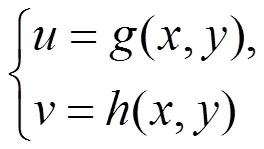
有连续偏导数，且存在唯一的反函数

其变换的雅可比行列式

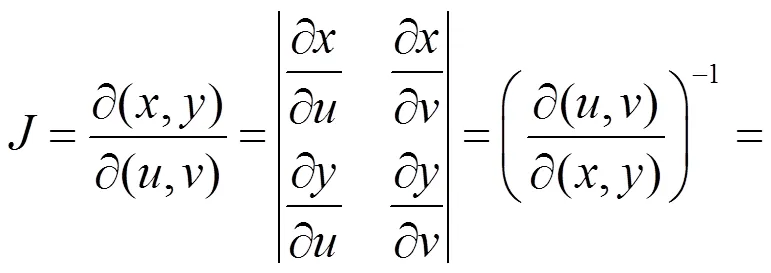
若

定理1的证明略。

这个方法也是目前人们研究二维随机变量到二维随机变量的变换的主要方法。这个方法虽然能适用于较多变量变换的情形，但是我们要指出，这个方法是存在一定的缺陷的：主要就是要求（1）式存在唯一的反函数，这个条件过强。我们往往会遇到（1）式的反函数是多值函数的情形。这个时候，定理1就不适用，这必然限制了定理1的应用。

1 主要结果

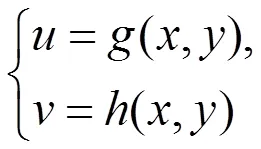
有连续偏导数，且存在一个反函数

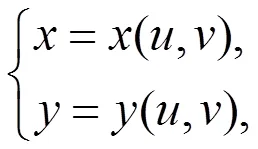
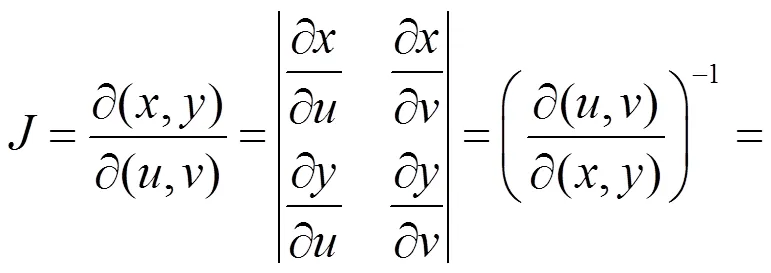
若

证明由二重积分的变量变换法，

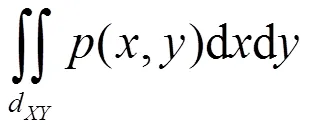
由（5）式，

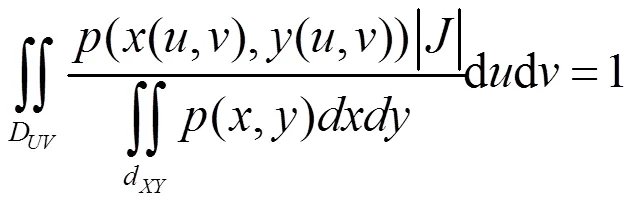
设

2 应用

下面应用定理2来求解一个例题。

解 由

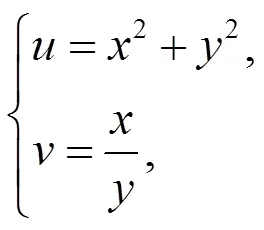
得

或

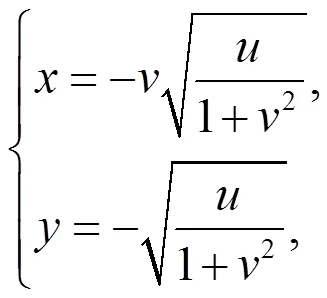
即（6）式的反函数是多值函数。我们选择其反函数之一（7），则知

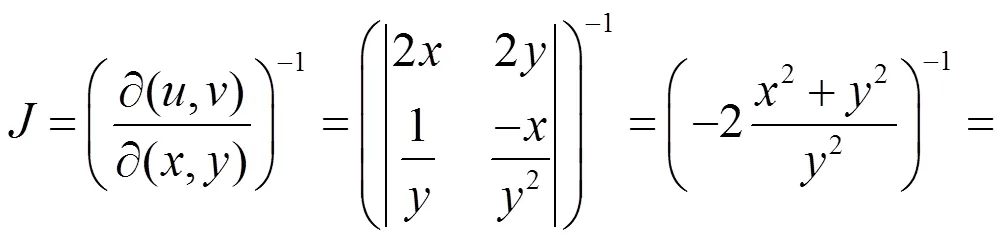
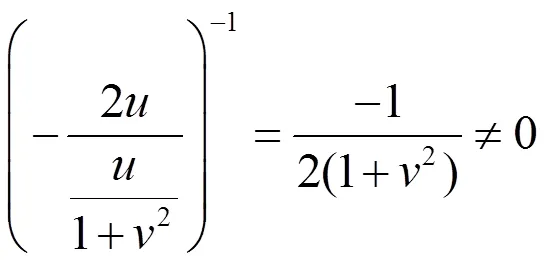
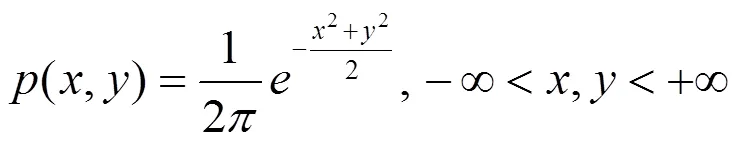
所以

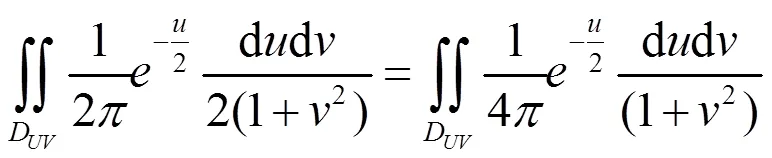
从而

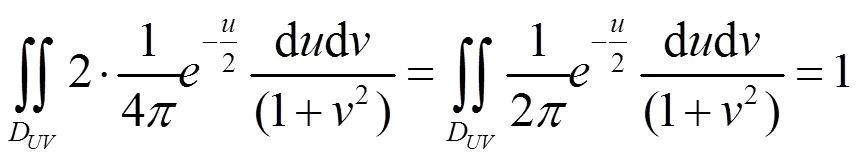
即

从而

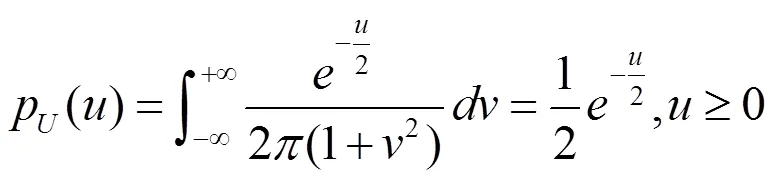
即

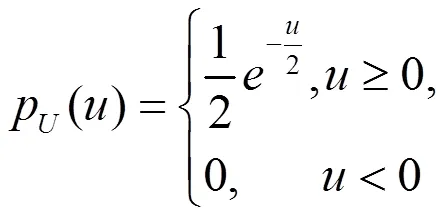
而

上例如用定理1是无法解决的，但用定理2却较容易解决，由此可见定理2在应用上的威力。我们要看到，定理1是定理2的特殊情形，定理2适用的范围更宽泛。

[1] 茆诗松,程依明,濮晓龙.概率论与数理统计[M].2版.北京:高等教育出版社,2012.

[2] 王凡彬,严雳.多维随机变量函数密度的求解方法[J].内江师范学院学报,2012,27(10):17-19.

[3] 李思齐,李昌兴,柳晓燕.二维连续型随机变量函数的分布密度的计算[J].大学数学,2011,27(5):162-166.

[4] 宋明娟,王悦姣.二维随机变量函数的概率密度公式[J].黑龙江科技学院学报,2011,2(5):422-424.

[5] 李香玲,刘桂霞.二维连续型随机变量函数的分布计算技巧[J].河北建筑工程学院学报,2003,21(3):67-69.

[6] 张洪川,盛克敏,马丽琼.一维与二维连续随机变量的函数的分布[J].西南民族大学学报:自然科学版,2005, 31(6):995-997.

[7] 顾玉娣.求连续型随机变量函数的概率密度[J].上海师范大学学报:自然科学版,2002,3(2):96-98.

[8] 马醒花,魏兰阁,彭宗勤.两个维随机变量函数的概率密度的求法[J].数学的实践与认识,2006,36(4)：174-177.

[9] 马军英.一类两个随机变量函数的分布[J].大学数学,2011,27(6):157-160.

[10] 杨秀妮,王雪芹.随机变量函数的分布问题 [J]．西安科技大学学报,2007,27(2):316-319.

PROMOTION OF VARIABLE TRANSFORMATION METHOD OF MULTIDIMENSIONAL RANDOM VARIABLE FUNCTION

WANG Fan-bin1,2

(1. College of Mathematics and Information Science，Neijiang Normal University，Neijiang , Sichuan 641100 ,China；2. Key Laboratory of Numerical Simulation in the Sichuan Province College，Neijiang , Sichuan 641100 ,China）

The current variable transformation method of multidimensional random variables function is discussed and its defect is overcome. Related properties which include density function method are applied. Furthermore, the current of the variable transformation method has been generalized to multi-valued function, which can use a variable transform of many-valued function. Application scope of the current variable transformation method is expanded and the application is also given.

multi-dimensional random variables; variables transform method; multi-valued function; promotion

O211.5

A

10.3969/j.issn.1674-8085.2013.03.003

1674-8085(2013)03-0010-03

2013-01-03；

2013-03-15

四川省高校数学与应用数学专业综合改革项目（O1249-1）；四川省高校数值仿真与数学实验教学示范中心项目（O1247）；四川省高等学校数值仿真重点实验室重点科研项目（09NJZZ001）

王凡彬(1957-)，男，四川富顺人，教授，主要从事偏微分方程及其应用研究(E-meil:wangfanbin@163.com).