由椭圆的发现看创新能力培养

●

(学军中学 浙江杭州 310012)

由椭圆的发现看创新能力培养

●闻杰

(学军中学 浙江杭州 310012)

1 由图形的演变发现椭圆的第一定义

课前，教师让每位学生准备1根绳子(线段)、2个图钉、1张硬纸板和1支铅笔.

开课时，首先让学生把线条对折后用一个图钉钉住分头的一端，另一头用铅笔画出轨迹图1(圆),让学生把线段的分头端稍微分开并用2个图钉钉住2端，再画轨迹图2(发现不圆了),继续把线段的分头端再分开大一些并用2个图钉钉住2端，画轨迹图3(发现更扁了)……一直到把线段拉直，画出的轨迹是线段为止.

图1 图2 图3

然后教师通过多媒体演示圆的轨迹，慢慢将圆心分离为2个点，此时圆会慢慢变扁.如果让点F1,F2关于中心点O对称移动，则画出的图像如图4所示.让学生观察，原圆上的点在直径A1A2的端点处保持不变，其他点随着点F1,F2的分离慢慢向直径压缩，图形慢慢变扁.

图4

由于圆上的动点P到圆心的距离的2倍，即2|PO|=|PO|+|PO|=2a不变，因此在分离点F1,F2的过程中轨迹圆变扁了，但|PF1|+|PF2|=2a没变.

此时，可因势利导让学生思考2个问题：

(1)这个扁圆上的点与原圆上的点否存在某些确定的关系？(y坐标按比例压缩.)

(2)联想圆的定义,你能归纳出扁圆的定义吗？(第一定义.)

结论当动点P到2个定点F1,F2的距离之和为定值2a(2a>|F1F2|)时，动点P的轨迹是扁圆，我们称之椭圆，这2个定点称为焦点(为什么称为“焦点”学生可能会感到疑惑，教师可以引导学生对“焦点的实际含义”作进一步的思考，事实上它与光学性质相关).

评注由圆的圆心分离成2个定点，并保持了|PF1|+|PF2|=2a不变，从而使圆演变成椭圆，这是一种创新，且从中探索出了椭圆的第一定义.整个过程学生一会激动，二会感到神奇，三会沉思.

激动的是：圆心分离后怎么轨迹变扁了.

神奇的是：这个扁圆上的点到2个定点的距离之和竟然不变.

沉思的是：这种现象能否从理论上给出证明.

2 由图形的几何特征类比椭圆方程

为了给出上述结论的理论证明，需要建立坐标系.可先让学生回顾圆方程的建立过程.

师：建立坐标系的目的是什么？怎样建立坐标系最合理？圆的标准方程为什么这么简洁？

对比“圆”(图5)，可以很快地在“椭圆”(图6)上建立直角坐标系.圆方程为x2+y2=a2，那么椭圆方程如何表示呢？

图5 图6

师：在“圆与椭圆”对应的坐标系下，圆方程已经知道，且很简洁，如何猜想椭圆的方程呢？

猜想不可盲目，要有一定的理论根据.可以先让学生独立思考，再相互讨论，然后一起分析探求.分析圆方程的特征与几何特征的关系如下：

(1)圆关于y轴对称，故有x的平方项x2，不应有x的一次项，否则不对称；

(2)圆关于x轴对称，故有y的平方项y2，不应有y的一次项，否则不对称；

(3)圆与x轴的交点为A1(-a,0)，A2(a,0),故当y=0时，有x2=a2；

(4)圆与y轴的交点为B1(0,-a)，B2(0,a),故当x=0时，有y2=a2；

(5)圆方程为：x2+y2=a2顺理成章，如图7所示.

再分析椭圆方程应该具有的特征与几何特征的关系如下：

(1)′椭圆关于y轴对称，故应有x的平方项x2，不应有x的一次项，否则不对称；

(2)′椭圆关于x轴对称，故应有y的平方项y2，不应有y的一次项，否则不对称；

(3)′椭圆与x轴的交点为A1(-a,0)，A2(a,0),故当y=0时，有x2=a2;

(4)′椭圆与y轴的交点为B1(-a,0)，B2(a,0),故当x=0时，有y2=b2;

(5)′椭圆方程是：________.

注：椭圆与y轴的交点可设为B1(0,-b),B2(0,b)，如图8所示.

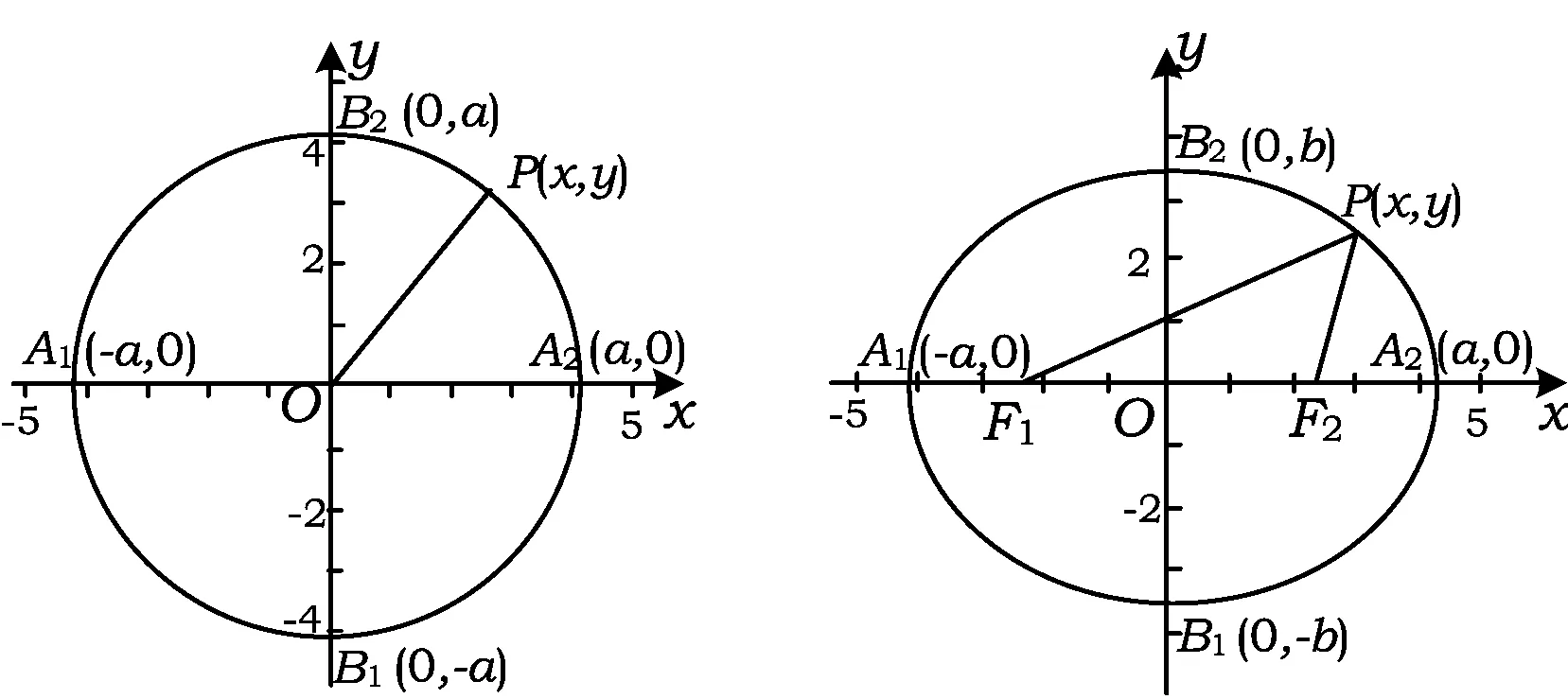
图7 图8

这种从圆的几何特征到椭圆的几何特征去分析对应方程的特征，然后通过类比得出未知曲线的方程是一种创新能力的体现，在教学中值得教师花时间去培养.

3 由方程的简化过程发现椭圆的第二定义

在图6的坐标系下，设焦点F1(-c)0，F2(c,0),则

方程(1)实质上就是椭圆方程，但是它的形式太复杂，几何特征不明显，使用不方便，故需要对其进行简化.化简方程的过程又是一次创新的机会，如何转化既快又好？

(让学生尝试讨论，独立化简，教师巡视.)

一般情况下学生可能会提出以下2种方法：

(1)移项平方法.把左边一个根式移到右边后，2边同时平方，再把其他项移到右边，留根式在左边，再2边同时平方，整理即可.

(2)直接平方法.2边直接平方，留根式在左边，其他项移到右边，再2边平方，并整理也可.

师：上述2种方法均可行，但运算量太大，运算过程也不美.其实有更好、更有效的方法，仔细观察式(1)的结构特征，发现左边的2个根式有很好的对称性，且又是齐次等系数根式，故可考虑分子有理化，即

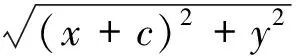
联立式(1),式(2)，得

式(1)-式(2),得

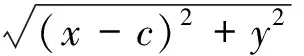
观察式(3)，还会有新的发现:等式左边是动点P到右边焦点F2的距离|PF2|，因此从“=”成立的意义考虑，右边也应该是距离，请同学们探索.

评注此处又是一个创新点，教师不要轻易放过，应让学生研究讨论.教师要相信学生无穷的智慧和力量，给予学生机会，让他们勇于尝试，不要一味地包办代替，抹杀学生的创新精神.

师生(一起分析)：一般情况下2个点的距离是“平方和”的形式,而式(3)的右边不是“平方和”的形式，怎么办?说明这是特殊的距离，如果式(3)改写为

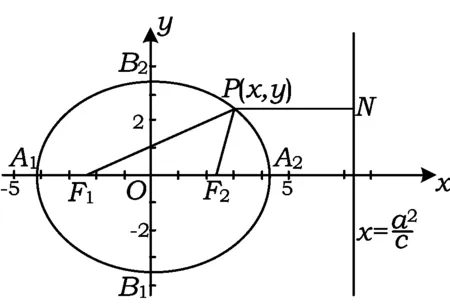
图9

这条定直线称为椭圆的“右准线”(为什么要称“准线”).此处，又埋下伏笔，引发学生思考.上式还可改写为

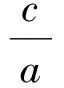
式(1)+式(2)，同理得到左焦点与左准线，即

化简得

评注这样的化简既对称又简洁，运算有美感.同时又能及时发现椭圆的第二定义.

对式(3)平方，由a2-c2=b2，化简得

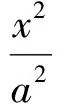
至此方程完璧归赵，与猜想完全吻合.

4 由对偶思想又可发现双曲线的定义

抓住时机，进一步引导，由上述的对偶运算还可以发散思维，如果把式(1)中根式间的“+”改成“-”会怎样？即方程改写为

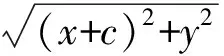
(1)′

曲线又会是怎样呢？

联想式(1)的分子有理化方法，同样可以对式(1)′的分子进行有理化，得

(2)′

式(2)′-式(1)′,得

式(2)′+式(1)′,得

评注用这种思路给学生上课，揭示了知识发生发展的原始轨迹，有一气呵成的感觉.整个过程教师牢牢地吸引住学生的思维，让他们始终处于积极的思考状态中，久而久之学生习惯了，就慢慢形成了创新意识.一个人如果有了创新意识，就会有创新精神，也就会有创新的动机，同时创新的能力也会慢慢得到培养.

5 拓展延伸

本节内容有很多创新的材料和机会，需要教师去把握、引导和运用.如可以布置动手操作的作业：

(1)你有更好的方法画出给定长轴和短轴的椭圆吗？

这些问题可以让学生在课外讨论解决，并在下节课上汇报、总结、点评.

6 教学随感

现行教学由于某种因素的影响变得有些功利化：教学知识时“去头掐尾取中间”，“去头”是去掉了“知识的发生、发展的原始轨迹”，“掐尾”是掐掉了“知识的拓展与延伸”，“取中间”也只是把书上的“定义、定理、公式”直接抛给了学生，致使学生没有创新意识，更无创新能力可言.

其实从创新思维的机制来看，一节课不必拘泥于几个环节(一堂课的基本环节)，达到几个目标(情感目标、思想目标、知识目标).关键在于：教师在这堂课中给予了学生什么；学生学到了什么；学生潜意识中的创造欲望是否被觉醒；观察、类比、联想、归纳等能力是否有所培养；创新意识、创新精神、实际动手能力是否有了提高；发散性思考问题的思维习惯是否有了改变；尝试探索的意识是否有了加强；整节课从开课到收尾是否环环相扣，牢牢抓住学生的注意力，让学生始终处于积极思维的状态中，给人一气呵成之感.

创新教育就要求师生之间应形成民主平等的和谐气氛，要为学生思考、探索、发现和创新提供最大的空间，使教学活动真正建立在学生自主活动和探索的基础上，进而形成有利于学生主体精神、创新能力健康发展的宽松的教学环境和教学体系.本堂课从一开始就放手让学生动手自主操作：画圆后分离圆心，观察、发现圆的变化与半径和的(焦半径和)不变，感悟出椭圆的第一定义.并继续放手让学生大胆从圆的几何特征和圆的标准方程的代数特征中类比出椭圆的几何特征和椭圆的标准方程的代数特征，从而猜想出椭圆的标准方程.这里因为给予了思维空间和时间学生才会有这种尝试探索的欲望，从而培养他们的创新能力.

在课堂教学中，允许学生与学生、学生与老师之间展开讨论，这能激活学生的创新思维.讨论的过程实质是相互竞争、相互诱导、相互激活的过程，学生的创新思维和想象在讨论中一旦被触发，有如激流奔放，甚至可以形成汹涌的创新思维浪潮.如本节课在化简椭圆方程前对方程形式的探求中，对椭圆方程化简过程的多种思维碰撞、讨论，对椭圆第二定义的发现等，均能吸引学生思考，拓宽思维的空间，激活学生从多角度、多层次去思考问题，迸发出创新思维的火花.

“问题是数学的心脏”，要培养学生的创新能力，首先要为学生创设好问题，何为好问题呢？就是所给的问题是学生熟悉的(原有知识基础上的延伸或是生活中的实际问题等)，精心设计问题情境，要通过问题情景的创设，打破学生的心理平衡，如本课把主动权完全交给学生在给予空间和时间的同时把一串问题链抛给学生：从圆怎样演变成椭圆——怎么发现椭圆的第一定义——从圆与椭圆几何特征的异同性类比猜想出椭圆标准方程——化简方程的过程优化——化简中的再思考再发现——椭圆第二定义的发现——椭圆标准方程的推出——对式(1)对偶式的思考——得出双曲线的第一定义……让学生的思维引起强烈的认知冲突，激发学生的学习兴趣和学习热情，调动学生学习的主动性、积极性和创造性，把学生作为一个整体发动起来.

最有效的学习应是让学生在体验和创造的过程中进行有意义的学习.数学课堂教学的关键是学生接受式学习与发展式学习互相补充、合理结合.数学学习的本质是学生获取数学知识、形成数学技能和能力的一种思维过程.“思考”是学生学习数学过程中的本质特点.如本课对方程的简化提出思考(分子有理化、对偶运算)，对化简后的式(3)提出几何背景的思考(得到椭圆第二定义)，对式(1)的结构提出对偶思考(得到双曲线定义)等.

学生的数学思维是对自身活动的反思，是对已有经验的反思.因此，我们应该把学生的数学思考作为整个数学学习活动的核心，更多地关注学生在思考什么、怎样思考的、思考的结果如何.笔者认为这样的课堂才是有效的、智慧的、精彩的!