“学”与“说”:数学思维的演绎课堂
——谈“三角形内切圆”的教学
●●
(江北区绿梅中学 浙江宁波 315000 ) (柯城区巨化中学 浙江衢州 324004)
“学”与“说”:数学思维的演绎课堂
——谈“三角形内切圆”的教学
●许土花●程阳清
(江北区绿梅中学 浙江宁波 315000 ) (柯城区巨化中学 浙江衢州 324004)
《初中数学课程标准》指出:学生是教学活动的主体,教学活动的开展是师生积极参与互动的过程,有效的教学活动更是学生的学与教师的教的有效统一.教学本身应该是“慢的艺术”,数学知识的发生发展需要学生去经历、去体会,也需要教师去理解、去感受学生存在的多样性与多面性.正是这些体现学生思考的东西才是数学课堂中教学生成的重要体现,是教师促进课堂效率,提升学生数学能力的空间.
而要了解知识在学生思维中如何发生发展,就需要学生用“说”来显性体现,这样也让学生之间的思维发展得以生成,产生新的思维火花.不同的思考与理解、相互间的对错关联,“说”出来才能得到知识的升华.笔者在九年级下学期的“三角形内切圆”教学中,搭建这样的平台放手让学生去“说”,充分展现学生多角度的思考过程,促进了学生的主动探索,提高了学生学习水平和数学思维能力.如何放手让学生“说”,“说”到什么程度,“说”到什么层面,以本课为例谈谈笔者的想法.
1 置疑——激发学生“说”的欲望
引课设问(1)有一个三角形,现要用一个圆形纸片来覆盖它,尽可能使纸片最小,请说明圆形纸片如何确定?
(2)有一个三角形,现要在三角形内裁出一个圆,且使圆的面积最大.
图1有几种设计,请同学们帮忙确定?
设计意图浙教版初中数学九年级下册教材中的“三角形内切圆”,引课用合作学习“从一块三角形上裁下一个半径尽可能大的圆来做玻璃圆桌的桌面,应该怎样画出裁剪图形呢?”其设计意图是:由这个实际问题引入本课内容,加强学生对所学内容必要性的认识,有利于创设良好的学习情境.
笔者基于教材的设计理念,在引入环节设计了第(1)问,这样的安排可以使课堂气氛更加活跃,通过2次不同的实验对比,使学生形成认知冲突,激发学生主动观察与思考,激发学生“说”的欲望,也激发学生自我探究的欲望,激活学生的数学思维.
2 观察——引导学生如何“说”
导课设问(1)怎样才能裁得最大圆,请观察:这时圆与三角形边的位置关系?
(2)三角形和圆各边相切,圆心在哪里?
(3)怎么找到这个圆的圆心与半径?
设计意图通过让学生观察、思考教学活动,激发学生的学习兴趣,使其主动观察并结合上节课学习的“直线与圆的位置关系”.学生很容易进入思考的状态,在教师积极引导设问下,学生学会了如何“说”,引出课题“三角形内切圆”.
导课思考再次引导学生观察、思考:假设三角形的内切圆图已画好(在分析作图题时,常假设图形已经画好,这样有直观借鉴,给分析思考带来方便).
(1)如图2,若⊙O与△ABC的各边相切,那么圆心O的位置有什么特点?
(2)怎样确定与三角形的3条边都相切的圆心位置?怎样确定半径的长?
(3)与一个三角形3条边都相切的圆有几个?
设计意图放手让学生自己动手画,让学生“说一说”内切圆的作法.
观察图中圆和三角形3条边的位置关系,尝试让学生“说一说”三角形内切圆的概念及性质?
观察图2和图3“说一说”:(1)名称;(2)确定圆心的方法;(3)各自的性质.
设计意图观察是提出问题、获取知识的首要步骤,在观察过程中进行适当的引导.理解三角形内切圆及圆的外切三角形的概念,引导学生采用类比的方法与三角形的外接圆及圆的内接三角形概念作比较.让学生畅所欲言,尽情地“说”,在说的过程中学生掌握了基础知识和基本技能,提高了解决问题的能力,也使数学思维得到发展.
3 放手——给学生“说”的权利
教师导语学习数学知识,就是为了解决实际问题.数学来源于生活,又应用于生活,让我们来解决一个实际问题.
问题1(课本例1)一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱.圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆.已知直三棱柱的底面等边三角形的边长为3 cm,求圆柱底面圆的半径.
(1)已知图形(课本图)是一个立体图,根据本题的题设和所求,你认为只要画出三视图中的哪一个视图,就能说明问题?
(放手尝试让学生自己抽象俯视图.)
(2)课本图中的⊙O与△ABC有何关系?怎样作出⊙O的半径?
(3)要计算半径OD的长,需要构造怎样的三角形?怎样添加辅助线?
(4)AO与∠BAC有何关系?AD与BD相等吗?根据什么?由Rt△AOD可求解吗?
问题2正三角形的内切圆:如图4,⊙O是正△ABC的内切圆,D,E,F是切点,若正△ABC的边长为6,
(1)求此内切圆的半径长;
(2)求正△ABC的面积.

图4 图5
问题3如图5,观察正△ABC的内切圆和外接圆.
(1)你有什么发现(2个圆的位置关系如何)?
(2)试求正△ABC的内切圆和外接圆半径之比.
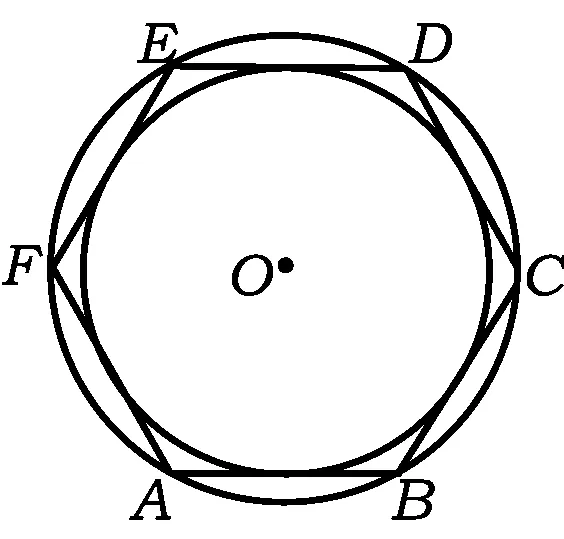
图6
问题4如图6,观察正六边形ABCDEF的内切圆和外接圆.
(1)你有什么发现(2个圆的位置关系如何?)
(2)试求正△ABC的内切圆和外接圆半径之比.
设计意图步步设问,以“问”启“思”,从而促“说”,给学生“说”的权利让学生“说”题.“说”题是一种讲解性理解,有助于提高学生的审题、析题能力.放手让学生说解题思路、方法、过程以及解题的经验体会、解题的注意事项等,提供对解决问题有针对性地“说”的一个空间.
4 释疑——提升学生“说”的品质
问题5如图7,⊙O是△ABC的内切圆,D,E,F是切点,设内切圆的半径为r,△ABC的3条边AB,BC,CA的长分别为a,b,c,则S△ABC=______.


图7 图8

教师导语(1)三角形周长l如何计算?
(2)运用三角形内切圆的定义及切线的性质分析:AE与AF,BE与BD,CD与CF分别有什么关系?你能证明吗?
设计意图在这个教学环节,让学生自己说给自己听,再在同伴间互相说,然后在小组内说,接着小组之间交叉说,最后面向全班学生和老师说.这样设计,让学生对自己感觉已经掌握的内容,在同学间说的过程中产生新的疑惑,然后在小组中说会产生新的思想方法,层层环节之后,教师对学生的“说”作个总结,提升到数学方法论上来.
问题7如图9,顶点与切点间的线段长与三角形3条边的关系:⊙I切△ABC的3条边于点D,E.F(注:让学生讨论,派代表“说”),则




图9 图10

“说”是课堂交流的一种重要方式,但“说”要能说出思想,说出思维的火花,说出能促进个体对知识的理解反思,这样“说”就促进了“学”.有一种好方法叫“放手”,给学生思考的余地,给学生思考的空间,真正把课堂还给学生.当然这一定要立足于课本,立足于课标,不能盲目而乱“说”,不能就题而说,不能就想而说,而是要在教学目标的基础上“说”,从而“说”出数学的思维.
既然数学是思维的体操,学生的“说”就是学生对数学思考的一种演绎,即在课堂中口头的表述,是学生展现自己的所学、所知、所惑.“言”为心之声,教师针对学生的“说”即时地有针对性释疑、引导,并不断层层递进,提升学生“说”的品质,不仅锻炼了学生的思维,而且上升到了学习数学知识的思想方法论上来,这何尝不是数学课堂所追求的一种高度?
[1] 章建跃.让学生在几何学习中学会认识和解决问题的方法[J].中学数学教学参考:中旬,2013(1/2):3-6.
[2] 刘东升.让学生在“讲题”中提高数学能力[J].中学数学教学参考:中旬,2011(7):7-9.
[3] 赵齐猛.一次意犹未尽的“数学活动”[J].中国数学教育,2009(11):23-26.

