理解概念熟练应用灵活构造
——谈自主招生考试中的导数备考
●
(绍兴市第一中学 浙江绍兴 312000)
理解概念熟练应用灵活构造
——谈自主招生考试中的导数备考
●虞金龙
(绍兴市第一中学 浙江绍兴 312000)
导数是中学教材中函数内容的一种重要补充,导数的概念和求导公式有许多独特的表现形式,因此也是自主招生中对基础知识和基本技能考查的重要内容之一,在自主招生备考时,应理解概念、熟练应用、灵活构造.
1 理解概念
主要包括理解导数的定义,熟记求导公式、导数的四则运算法则、复合函数求导法则,并能运用上述公式与法则进行求导计算.

(2000年上海交通大学自主招生试题)
解由导数定义知



(2008年华约自主招生试题)
解由已知得
…
累加得
即

评注本题主要考查导数定义式中极限的概念.
例3已知f(x)满足:f(x+y)=f(x)+f(y)+xy(x+y),又f′(0)=1,求函数f(x)的解析式.
(2000年上海交通大学自主招生试题)
解取x=y=0,则f(0)=0.令x=y≠0,则
从而


(1)
由f′(0)=1知,对a∈R,有
在式(1)中,令n→+∞,则

即

且当x=0时,f(0)=0.

例4过点(-1,1)的直线l与曲线y=x3-x2-2x+1相切,且(-1,1)不是切点,则直线l的斜率是
( )
A.2 B.1 C.-1 D.-2
(2011年华约自主招生试题)
解设曲线的切线(即直线l)的切点为P(x0,y0),则由导线的几何意义得,直线l的斜率为
从而直线l的方程为

因为直线l过点(-1,1),所以

又因为点P(x0,y0)在曲线上,所以
式(2)+式(3),得
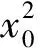
即
亦即
因此x0=1,k=-1.故选C.
2 熟练应用
主要包括利用导数确定函数的单调性、求函数的极值与最值,特别是能用导数的方法解决关于函数性质的综合性问题.
例5现有如下2个命题:
命题p:函数f(x)=x3+ax2+ax-a既有极大值,又有极小值;
命题q:直线3x+4y-2=0与曲线x2-2ax+y2+a2-1=0有公共点.
若命题p或q为真,且命题p且q为假,试求a的取值范围.
(2009年浙江大学自主招生试题)
解命题p:由f(x)=x3+ax2+ax-a,知f′(x)=3x2+2ax+a.f(x)既有极大值,又有极小值,即f′(x)有2个不同的零点,即Δ=(2a)2-12a>0,解得a>3或a<0.因此,当a>3或a<0时,命题p为真.



评注命题p:函数f(x)=x3+ax2+ax-a既有极大值,又有极小值的等价条件是f′(x)=0有2个不同的零点,从而去求出命题p为真时a的取值范围.
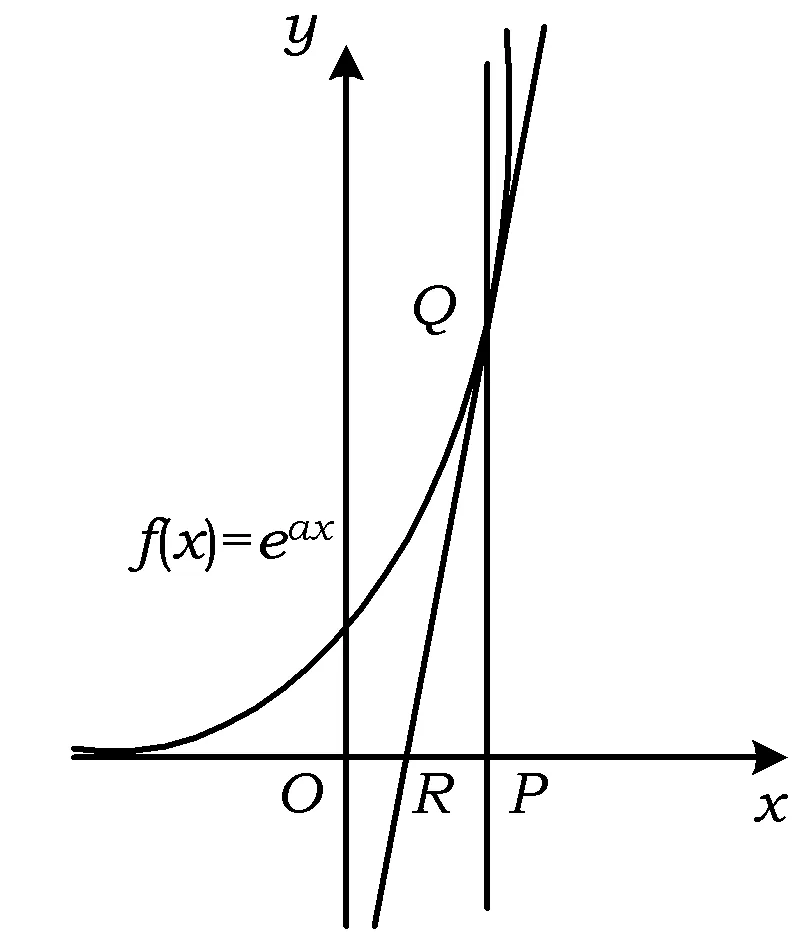
图1
例6设f(x)=eax(a>0),过点P(a,0)且平行于y轴的直线与曲线C:y=f(x)的交点为Q,曲线C过点Q的切线交x轴于点R,则△PQR的面积的最小值为
( )
(2010年华约自主招生试题)


评注求函数导数时要运算准确,本题是复合函数求导,表示出三角形面积函数之后,再次求导,求出函数的最小值,把抽象的问题转化为具体、熟悉的问题,数形结合,相得益彰.

(1)若f′(x)+7a=0有2个相等实根,求f′(x)的解析式;
(2)f(x)在R上单调递减,求a的范围.
(2009年华约自主招生试题)

f′(x)=ax2+2bx+c,
即
f′(x)+9x=ax2+2bx+c+9x.

2b=-3a-9,c=2a.
因为f′(x)+7a=ax2-(3a+9)x+9a=0,f′(x)+7a=0有2个相等的实根,所以
Δ=(3a+9)2-36a2=0,
整理得
a2-2a-3=0,
解得
a=-1或a=3(舍去),
从而
2b=-6,c=-2,
即
f′(x)=-x2-6x-2.
(2)由第(1)小题,知f′(x)=ax2+2bx+c=ax2-(3a+9)x+2a,要使f(x)在R上单调递减,只需满足ax2-(3a+9)x+2a≤0在R上恒成立即可,故
解得a的范围为

评注本题考查三次函数的导数、极值点及单调性的应用,是高考和自主招生相接轨的基本问题之一.
例8设a为正数,f(x)=x3-2ax2+a2,若f(x)在区间(0,a)上大于0,则a的取值范围是
( )
A.(0,1] B.(0,1) C.(1,+∞) D.[1,+∞)
(2011年复旦大学自主招生试题)

评注本题主要应用导数分析函数f(x) 的单调性和最值情况,解题的关键点在于借助导数分析出函数f(x)在(0,a)上为减函数,再解一个三次不等式即可.
例9已知函数f(x)=x3+ax2+bx+c.
(1)当b=1时,若函数f(x)在(0,1]上为增函数,求实数a的最小值.

(2010年中南财经政法大学自主招生试题)
解(1)当b=1时,f′(x)=3x2+2ax+1在x∈(0,1]上恒有f′(x)≥0,从而


即
亦即
因此
x1=-2x0或x1=x0(舍去).

评注本题主要考查学生是否能用导数的方法解决一些函数性质的综合性问题.
3 灵活构造
在自主招生考试中,还需要学生掌握一种重要的解题方法——构造函数解决问题.该方法往往难度大,涉及面广,灵活性强,需要不断尝试与探索.

(2010年南开大学自主招生试题)

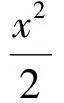
于是
f″(x)=-sinx+x.

评注此例是最常见的构造函数的问题,求导以后,很自然地得到所要构造的函数.

(2003年中国科学技术大学自主招生试题)

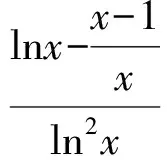
令g(x)=xlnx-(x-1),则
g′(x)=lnx+1-1=lnx,

g(x)=xlnx-(x-1)>g(1)=0,
从而

由此可得f(x)严格单调递增.
评注此例的关键是将指数式转化为对数式,然后构造函数来证明,有一定的难度.

(2009年华约自主招生试题)
证明构造函数y=f(x)=x2n,n∈N*,因为y′=2nx2n-1,y″=2n(2n-1)x2n-2≥0,所以f(x)是(-∞,+∞)上的凹函数,于是
即

此例可推广为更一般的结论:
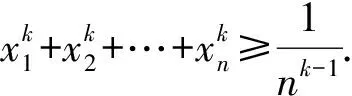
证明因为f(x)=xk(x∈(0,+∞),k≥1),当k=1时,f″(x)=0,当k>1时,f″(x)=k(k-1)xk-2≥0,即f(x)=xk(x∈(0,+∞),k≥1)是凹函数.由琴生不等式
得
评注该题推广后,难度和灵活度更大了,达到了数学竞赛试题的难度.
从历年的自主招生试题来看,对导数的考查频率较高,而且考查难度较大.备考时要以不变应万变,以理解概念为本,熟练运用导数的知识掌握常规的问题,特别要多在利用函数构造法方面下功夫,才能取得更好的成绩.

