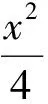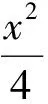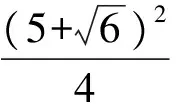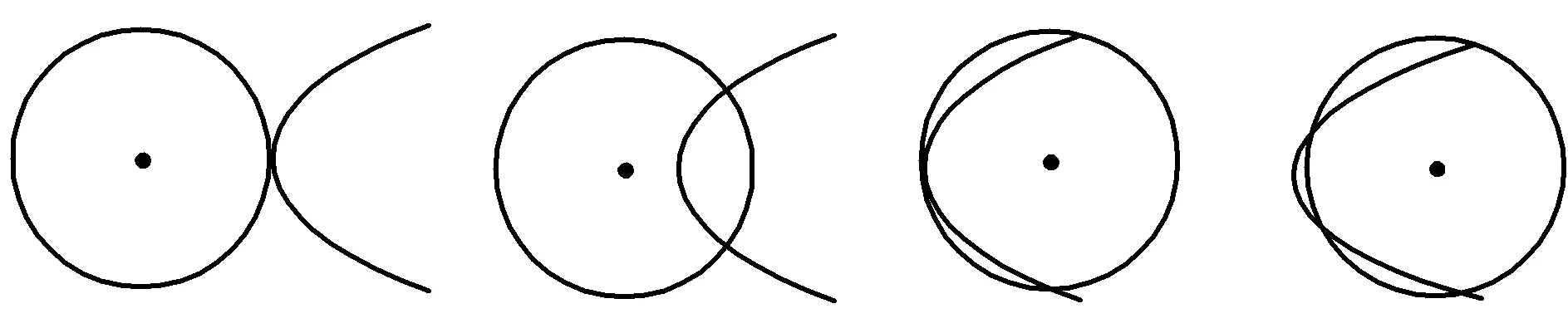判别式为何失效了
——关于圆与圆锥曲线相切的问题
●
(杭州市第十四中学 浙江杭州 310015)
判别式为何失效了
——关于圆与圆锥曲线相切的问题
●朱微
(杭州市第十四中学 浙江杭州 310015)
1 起:看似巧妙,却得到了错解
近日,笔者在课堂上给学生出了2道题.
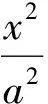

|PN|2=x2+(y-3)2=-(y+3)2+2b2+18,
其中-b≤y≤b.
当0 b2+6b+9=50, 当b≥3时,|PN|2有最大值2b2+18.从而 2b2+18=50, 解得b=4. (1) 得y2+6y+41-2b2=0, (2) 从而 Δ=8(b2-16)=0, 解法1利用含参数的二次函数在固定区间上求最值的方法,需要分类讨论,计算繁琐.解法2灵活应用数形结合,计算简洁,受到了学生的欢迎.但是,在例2中,解法2却受到了质疑. 解(数形结合法)由题意,联立方程组 (3) 消去y得 5x2-18ax+9(a2+3)=0, (4) 从而Δ=36(4a2-15)=0, (5) 解得 如果把结果代回检验,会发现这是个错解.这道题的正解应为a=2或a=4.为什么对例1适用的好方法,在例2中却是错解呢?究竟是方法的错误还是我们用错了方法呢? 想到这里,笔者不禁对以前用代数法判断直线与圆锥曲线的位置关系产生了怀疑.不妨以椭圆与直线为例,联立方程组 得 2种消元变形中,x和y的取值范围都被保留着,因此无需单独说明. 圆锥曲线又称二次曲线.从代数的角度来看,2条圆锥曲线以及圆锥曲线与直线的交点问题,都是通过联立方程,消元得到一个关于x(或y)的二次方程,当Δx(或Δy)=0,二次方程有2个相同的实数根时,2条曲线有二重交点(即切点). 消去y得 55x2-128ax+(64a2+17)=0, 从而 Δ=4·(64·9a2-55·17)=0, 解得 图1图2图3图4 状态3当圆M沿x轴继续向右平移时,2条曲线相交.由Δ>0得到2个解,再根据对称性,得到4个交点A,A′,B,B′(如图3). 状态4圆M继续右移,2个交点B,B′越来越接近,最后重合,成为了一个切点.交点A,A′还存在.此时,圆M部分在椭圆C内,部分在椭圆C外(如图4). 状态5,6圆M继续右移点B附近,2条曲线相交(如图5);交点A,A′越来越接近,最后重合,再次成为切点,此时圆M外切于椭圆(如图6). 图5 图6 图7 状态72条曲线外离,无公共点(如图7). 图8 再看例2的过程图(如图8),它经历了内含、内切(1个切点)、相交(2个关于x轴对称的交点)、外切(1个切点)、外离5个状态.观察图像易知,关于x的二次方程(4)不可能存在二重根,只有内切和外切2种状态符合题意. 经过上述分析我们发现,圆与圆锥曲线相切(包括圆锥曲线之间)是个复杂的问题,切点可能是关于x的二重根,也可能是关于y的二重根.而2条曲线方程联立时,为方便起见,一般得到的是关于x或y的二次方程.因此,只用Δ还不够,还要结合过程图来分析.这部分内容教材没有出现,教师在给学生讲解时要慎重.如果学生用了该方法,也要提醒学生多画图,多检验. 最后,让我们在来做个巩固练习. 即 5x2-40x+4(19-λ)=0. 图9 总之,双曲线的方程为 [1] 杨华.争鸣:问题207评析[J].数学通讯,2012(1):31-33. [2] 卫福山.争鸣:问题221[J].数学通讯,2012(12):31.
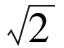
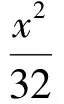
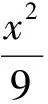
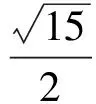
2 承:仔细思考,原来变形并非等价
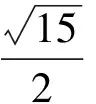
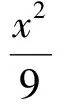
3 转:追根溯源,究竟何为相切
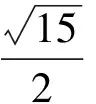
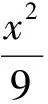
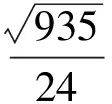
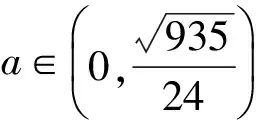


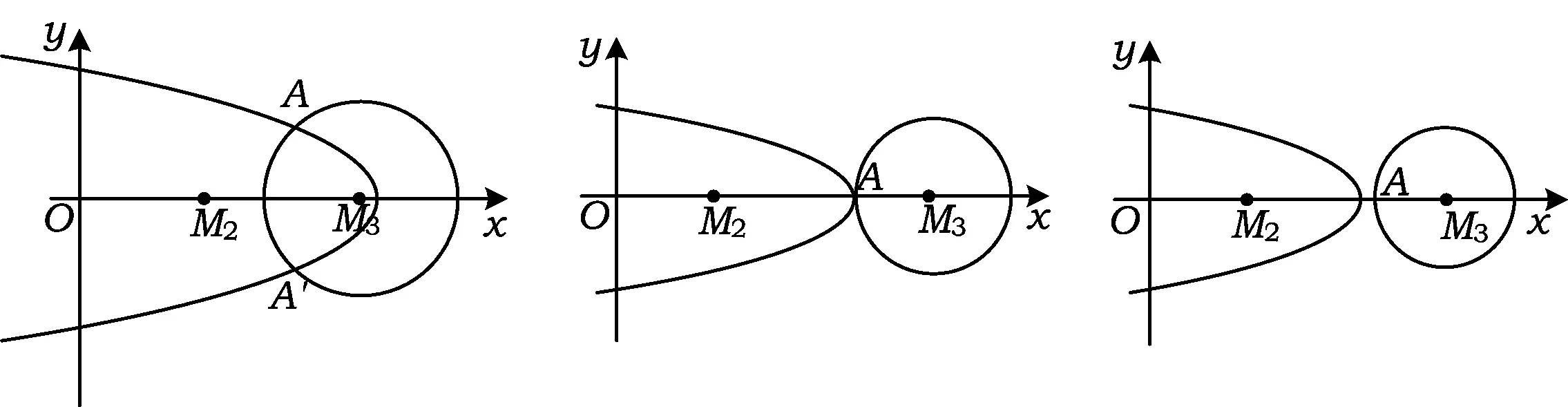
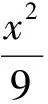

4 合:圆锥曲线若相切,数形结合不容易