无序对准一维矢势束缚中无质量Dirac电子的影响*

宋世英， 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

无序对准一维矢势束缚中无质量Dirac电子的影响*

宋世英， 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

通过有限差分的方法，数值计算了一个相对论性质的Dirac电子在磁场和无序同时存在时的能谱结构，并讨论了不同磁场强度和无序强度时电子密度分布的变化情况.结果发现:随着无序强度的增大，无序势削弱了磁场对电子的捕获，使局域化现象减弱，使得无质量Dirac电子出现了有别于Anderson局域化的现象.

无序；一维；Dirac电子；电子密度分布

0 引 言

2004年,曼彻斯特大学物理学家Novoselov和Geim等[1]在实验室中首次成功地从石墨中分离出石墨烯.由于单层石墨烯中的准粒子是无质量的Dirac费米子[2]，其低能激发具有线性的色散关系，粒子遵循相对论性量子力学，可以用Klein-Gorden方程和Dirac方程描述.另外，在原子核物理和其他领域中，研究这些方程的束缚态解也有着重要的实际意义.由于石墨烯在实验上的实现，近几十年来理论物理学者开始广泛关注二维单层石墨烯中的相对论性电子低能谱的相关性质[3].随着单层石墨烯中准Dirac电子的发现了[2,4]，科学家们也相继在光晶格的冷原子[5]和三维拓扑绝缘体中发现了准Dirac电子.通过对Dirac电子在不同外势情况下电子性质的研究，发现Dirac电子在静电势中可以像相对论粒子那样无阻碍地穿过任意高和宽的势垒[3].对相对论性粒子的囚禁可以通过具有无穷质量边界的量子点或外加磁场来实现.

石墨烯的材料中普遍存在着无序，无序和电子间的相互作用对理解众多实验现象有着非常重要的意义.非相对论性的电子在无序中的性质由Anderson等[6]在1958年提出的局域化理论来解释，其局域态电子的波函数随着距离的增大呈指数衰减.对无序性质理解的加深，又激起了物理学者对无序系统中电子输运性质的研究[7-12].目前，随着众多的准Dirac电子材料的发现，如何理解相对论性材料中无序对体系的影响无疑也具有重要的现实意义.当囚禁Dirac电子的磁场和无序共同存在时，系统的能谱结构、电子密度分布如何变化则是我们目前感兴趣的问题.

本文主要研究了石墨烯费米面附近的电子，通过数值求解磁场中的Dirac方程，并考虑不同的无序强度对电子性质的影响，得到了无质量的Dirac电子在磁场和无序势共同存在时表现出的一些局域和非局域性质.发现随着无序强度的增大，电子密度分布几率降低，分布呈展宽现象，表现出弱局域化现象.

1 理论模型

石墨烯的主要性质是由费米面附近的电子行为决定的.本文主要研究单层石墨烯的一个电子(忽略电子自旋)在Dirac点(K和K′)附近的性质.在垂直于石墨烯的磁场和无序的共同作用下，系统的哈密顿量可表示为[13]

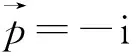
综上,可以得到不含时的无质量Dirac-Weyl方程为

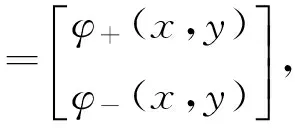
把式(3)代入方程(2)可以得到2个耦合的本征方程组

由方程组(5)可以定义一个包含磁场贡献的有效势为

通过有效势的公式,可以大致了解到Dirac粒子密度分布的基本性质.而数值上求解的是通过对方程(4)进行无量纲变换得到的耦合方程组

2 计算方法

采用有限差分的方法，考虑锯齿形边界条件

将耦合方程组(7)进行如下变换：

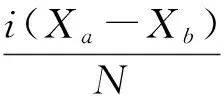
3 数值结果和讨论

利用有限差分的方法，通过数值求解方程(9)可得到Dirac电子在磁场矢势和无序外势中的密度分布情况，而密度分布是可以通过实验直接测量的物理量，对其进行研究可以同实验结果进行直接对比.

当无序势V1(X)=0，即无序强度g为零时，磁场产生的有效势V±eff(X)随磁场强度衰减系数γ的变化情况和此时系统最低4个能级的电子密度ρn(n=0,1,2,3)分布情况分别如图1(a),(b)和图2(a),(b)所示(其中Dirac电子在不同能级n时的电子密度分布ρn=Ψ*n(x)Ψn(x)，n=0,1,2,3,…,n).

图1(a),(b)是有效矢势V+eff(实线)和V-eff(虚线)在不同强度的磁场衰减系数下的分布情况.指数衰减磁场在系统中形成了量子阱，从而可以形成束缚态.由图1(a)可以看出,对于弱非均匀性(γ=0.01)磁场下产生的有效势关于X轴的分布是对称的，而对于强非均匀性(γ=0.5)磁场下产生的有效势关于X轴的分布是非对称的，见图1(b).γ越小，磁场的非均匀性越小，当γ→0时，系统在均匀磁场下处于Landau能级中；γ越大,束缚态能级越少，当γ→∞时，系统处于自由粒子的运动状态.

(a)在弱磁场衰减系数γ=0.01时的分布 (b)在强磁场衰减系数γ=0.5时的分布

图1 包含磁场贡献的有效势分布图

图2(a)和(b)给出了图1(a)和(b)相对应的不同能级下的密度分布.可以看出,电子的密度分布在对称的有效势下保持对称性，在非对称的有效势下，电子的密度分布呈现出非对称性.随着磁场衰减系数的增大，电子密度分布的对称性消失.

当系统中存在无序时，随着无序强度g的增大，电子密度分布出现明显的变化.由图3(a),(c)或(b),(d)可知,随着无序强度g的增大，电子的密度分布呈现展宽的趋势.在磁场和无序的共同作用下，相对论性的Dirac电子被无序形成的势能低点所捕获，从而出现去局域化效应，电子的密度分布出现扩展态的形式，这不同于相对论性的Anderson局域化现象.

(a)在弱磁场强度衰减系数γ=0.01时的分布 (b)在强磁场强度衰减系数γ=0.5时的分布

图2 不同能级对应的电子密度分布

在弱磁场衰减系数下，由图3(a)和(c)可知，无序对相对论性Dirac电子的密度分布影响不大，因为此时的有效势具有相对较低的势能零点，从而Dirac电子主要被捕获在X=0附近的位置，无序使其分布略微展宽.在强磁场衰减系数下，由图3(b)和(d)可知，无序对相对论性的Dirac电子的密度分布影响随无序强度的增强而变大，因为此时的有效势具有相对较高的势能零点，无序使得更多的势能低点出现.在此影响下基态密度分布展宽，在X=0处的密度从g=0时的0.55下降到g=5时的0.51；而对激发态的电子密度分布影响更大，使相应的密度分布弥散于整个空间.

(a)在弱磁场衰减系数γ=0.01，无序强度g=5时的分布 (b)在强磁场衰减系数γ=0.5，无序强度g=1时的分布

(c)在弱磁场衰减系数γ=0.01，无序强度g= 10的分布 (d)在强磁场衰减系数γ=0.5，无序强度为g= 5时的分布

图3 不同能级在磁场和无序共同作用下对应的电子密度分布

图4给出了第一激发态在弱磁场衰减系数γ=0.01且不同无序强度时电子的密度分布情况.图4更清晰地反映出随着无序强度g的增大，电子密度分布出现去局域化效应的现象(在弱磁场衰减系数γ=0.01时，n=1的第一激发态在无序强度g分别为0,5,10时的电子密度分布).

由于相对论性Dirac电子的Klein佯谬，一般的外势是不能捕获电子的.笔者的数值计算结果表明，即使是很小的衰减磁场也可以捕获相对论性的Dirac电子，而无序的出现使得Dirac电子具有扩展态的性质，电子分布于更大的空间区域，无序势使得相对论性Dirac电子具有去局域化的趋势.目前的研究可以推广到更复杂的有限外势的研究，如研究双曲磁场，或线性磁场，或以上不同磁场的综合因素下，无序对Dirac电子的影响，以及在考虑了自旋-轨道耦合情况下，无序对Dirac电子基态性质的影响.另外,在无序和相互作用的共同作用下，系统基态和激发态的变化，无疑也是个有意义的研究课题.

图4 第一激发态在不同无序强度时对应的电子密度分布

4 结 论

基于有限差分，通过求解在磁场和无序同时存在时的准一维无质量相对论性Dirac电子，得到了不同磁场强度和无序强度时系统电子密度分布的情况.发现当无序强度g=0时，磁场产生的有效势可以捕获相对论性Dirac电子；随着无序的增强，即无序强度g的增大，电子的密度分布发生了变化，Dirac电子的密度分布呈展宽现象；无序的出现使得Dirac电子具有扩展态的性质，电子分布于更广的空间区域，无序势使得磁场中相对论性Dirac电子具有去局域化的趋势.

[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.

[2]Neto A H C,Guinea F,Peres N M R,et al.The electronic properties of graphene[J].Rev Mod Phys,2009,81(1):109-162.

[3] Pereira J M,MlinarJr V,Peeters F M,et al.Confined states and direction-dependent transmission in graphene quantum wells[J].Phys Rev B,2006,74(4):045424.

[4] Abedpour N,Esmailpour A,Asgari R,et al.Conductance of a disordered graphene superlattice[J].Phys Rev B,2009,79(16):165412.

[5]Juzeliūnas G,Ruseckas J,Lindberg M,et al.Quasirelativistic behavior of cold atoms in light fields[J].Phys Rev A,2008,77(1):011802(R).

[6]Anderson P W.Absence of diffusion in certain random lattices[J].Phys Rev,1958,109(5):1492- 1496.

[7]Cheianov V V,Fal′ko V I.Selective transmission of Dirac electrons and ballistic magnetoresistance ofn-pjunctions in grapheme[J].Phys Rev B,2006,74(4):041403.

[8]Abrahams E,Anderson P W,Licciardello D C,et al.Scaling theory of localization:absence of quantum diffusion in two dimensions[J].Phys Rev Lett,1979,42(10):673-676.

[9]Anderson P W,Thouiess D J,Abraharns E,et al.New method for a scaling theory of localization[J].Phys Rev B,1980,22(8):3519-3526.

[10]Zhu Shiliang,Zhang Danwei,Wang Z D.Delocalization of relativistic Dirac particles in disordered one-dimensional systems[J].Phys Rev Lett,2009,102(21):210403.

[11]Yuan Jianhui,Cheng Ze,Yin Miao,et al.Klein paradox and disorder-induced delocalization of Dirac quasiparticles in one-dimensional systems[J].Phys, 2010,54(6):1129-1133.

[12]Krekora P,Su Q,Grobe R.Relativistic electron localization and the lack of zitterbewegung[J].Phys Rev Lett,2004,93(4):043004.

[13]Schnez S,Ensslin K,Sigrist M,et al.Analytic model of the energy spectrum of a graphene quantum dot in a perpendicular magnetic field[J].Phys Rev B,2008,78(19):195427.

[14]Handrich K.Quantum mechanical magnetic-field-gradient drift velocity:an analytically solvable model[J].Phys Rev B,2005,72(16):161308.

(责任编辑 杜利民)

TheeffectsofdisorderonmasslessDiracelectroninaone-dimensionalvectorconfinement

SONG Shiying， GAO Xianlong

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was numerically calculated the structure of energy spectrum and the electron density distribution of a Dirac electron in the present of a magnetic field and disorder by using the method of the finite difference. The effect of the different magnetic fields and disorder on the electron density distributions were also discussed. With the increase of disorder strength, disorder gradually weakensed the localization of the electron and made the massless Dirac electron delocalized which was different from the Anderson localization theory.

disorder; one dimension; Dirac electron; electron density distribution

O441.4

A

1001-5051(2013)01-0068-06

2012-03-06

国家自然科学基金资助项目 (10974181)

宋世英(1986-)，女，河南周口人，硕士研究生.研究方向：低维无序相对论电子的性质.

高先龙.E-mail: gaoxl@zjnu.cn