弯曲对扶手椅型石墨烯纳米带电子性质的影响*
黄 琼, 童国平
(浙江师范大学 凝聚态物理研究所,浙江 金华 321004)
弯曲对扶手椅型石墨烯纳米带电子性质的影响*
黄 琼, 童国平
(浙江师范大学 凝聚态物理研究所,浙江 金华 321004)
石墨烯纳米带并不是一个完全平整的结构,而是一个准平面结构.为了研究非平整对石墨烯纳米带电子结构的影响,利用紧束缚方法和轨道杂化理论,研究了弯曲对扶手椅型石墨烯纳米带电子结构的影响.计算结果表明:扶手椅型石墨烯纳米带电子性质与弯曲的程度有关,且在高能部分影响较大;当纳米带的宽度一定时,随着弯曲程度的增加,能带的带隙随之增加.
紧束缚;弯曲;石墨烯纳米带;能带结构
0 引 言
长期以来,以二维形式存在的碳材料一直被人们以为是不存在的[1-3],直到2004年,英国曼彻斯特大学Novoselov与Geim等[4]用机械剥离的方法成功制备了石墨烯,人们才初步认识了这种材料.石墨烯因具有许多奇特的物理性质而引起科学家的广泛关注,如半整数量子霍尔效应[5-8]、klein 遂穿[9]等.而石墨烯纳米带是在二维石墨烯的基础上经过一定方法剪裁得到的带状结构,从几何结构上可分为扶手椅型和锯齿型2类.前人已对平整的石墨烯纳米带在理论上做了较多的研究,结果显示,锯齿型石墨烯纳米带呈金属性[10-12],而扶手椅型的电子性质和它的宽度有关,具有金属和绝缘体2种类型[10-13].由于边缘应力的作用,独立式的石墨烯纳米带将会产生起伏使其成为一个准二维的结构[14],而这种对平面结构的破坏必将对石墨烯纳米带的电子性质带来影响.对非平整的石墨烯及纳米带的物理性质已有不同方法的理论研究[15-16],但一般计算量较大.紧束缚方法的特点是能大大减小计算量,同时给出和第一性原理相符的结果[17-18].本文主要考虑扶手椅型石墨烯纳米带翘起成半圆柱形的情况,利用紧束缚模型和轨道杂化理论,详细讨论了弯曲对扶手椅型石墨烯纳米带的影响.
1 理论方法和模型
考虑将扶手椅型石墨烯纳米带弯曲成半圆柱形,如图1所示.

图1 将扶手椅型石墨烯纳米带沿受限宽度方向为径向卷曲成半圆柱形
对于非平整石墨烯纳米带,假设沿长度方向依然存在周期性,仿照平整扶手椅型石墨烯纳米带[18],波函数可以写成
式(1)中,
式(2)中,c代表π轨道的s成分,因为弯曲导致石墨烯纳米带形成sp3杂化,若取c为零,则式(2)退化为平整扶手椅型石墨烯纳米带的波函数.|Aij>s和|Aij>pz分别表示A子晶格中电子的s轨道和pz轨道的波函数,|Bij>s和|Bij>pz分别表示B子晶格中电子的s轨道和pz轨道的波函数.φ(i)表示波函数在受限宽度方向的分量,采用固定性边界条件.
另一方面,由于弯曲,π轨道不再和表面垂直,会和径向形成一个夹角[19]

式(3)中:a是相邻碳原子键长;r为曲率半径.而π轨道的s成分可表示为
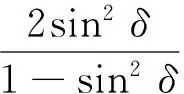
将波函数代入薛定谔方程,可得石墨烯纳米带的能谱为
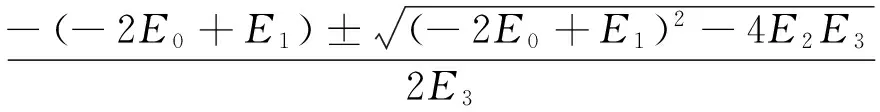
式(5)中,
式(6)中交叠积分s0取为零,而r0和f由下式给出

式(7)中,
tpp=pz
(8)
tpp,tsp,tss分别表示最近邻电子的跳跃积分的分量.在所有计算中,设定参数ε=-0.36 eV,tpp=-2.78 eV,tss=-1.12 eV,tsp=-1.12 eV,其中ε,tpp由文献[15]给出.
2 讨论与分析
为了对比,笔者计算了平整扶手椅型石墨烯纳米带和半圆柱形扶手椅型石墨烯纳米带的能带结构,计算结果如图2所示.
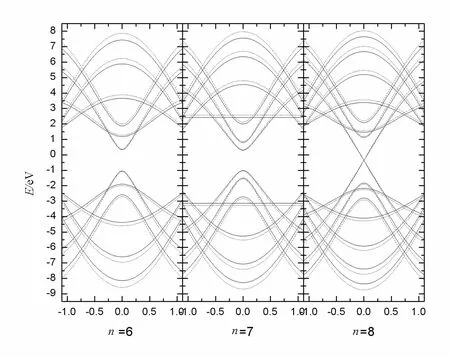
虚线代表平整的纳米带;实线代表半圆柱形的纳米带
由图2(虚线)可知:平整的扶手椅型石墨烯纳米带的能带结构和宽度有很大关系,当宽度为6和7时,纳米带表现为绝缘性;而当宽度为8时,表现为金属性.当宽度为7时,能带出现水平的导带和价带,能量与x方向的波矢无关,表现为范霍夫奇性,这也反映在宽度为7的纳米带的态密度中.通过其他不同宽度的计算,可以得出结论,纳米带分为宽度n=3m,n=3m+1,n=3m+2这3种结构,这里m为整数.对比弯曲后的纳米带的能带结构(实线),可以明显地看出弯曲对能带结构的影响.改变主要体现在能带的带宽部分,通过弯曲,带宽均有减小,但是对能带的带隙也有较小的影响.通过对比可以看出,虽然弯曲对纳米带的能带结构带来影响,但是纳米带对宽度的依赖并不因为弯曲而改变.这些性质也可以从两者态密度的对比中看出,如图3所示.由图3可以看出:当能量为-2.5 ~2.5 eV时,两者态密度基本重合;当宽度为7时,两者态密度出现了2个高峰.事实上,当宽度方向量子数P满足p/(n+1)=1/2时,能带就会出现水平导带和价带.

虚线代表平整的纳米带;实线代表半圆柱形的纳米带
为了显示弯曲程度对扶手椅型石墨烯纳米带能带结构的影响,笔者计算了宽度分别为6和7时不同弯曲程度下的能带带隙,其中弯曲程度用弯曲后的圆心角θ表示,当θ=π时,即弯曲成半圆柱形,计算结果如图4表示.
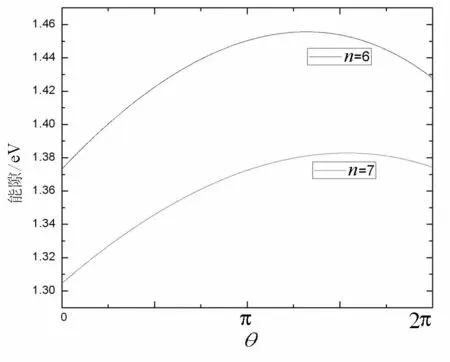
图4 宽度为6和7的扶手椅型石墨烯纳米带能带带隙随弯曲程度的变化
由图4可以看出,当宽度固定时,在弯曲程度从无到半圆柱形的过程中,随着弯曲程度的变大,能带带隙也随之增大,这个改变主要来自于π电子中s成分的变化,当弯曲超过一定限度时,能带带隙又开始随之减小.可见弯曲程度对能带带隙有较明显的影响.
3 结 论
当扶手椅型石墨烯纳米带被弯曲后,形成sp3杂化,π电子中将存在s轨道成分,并且π轨道会和径向产生一个偏角,这些都会随着弯曲程度的改变而改变,并影响弯曲扶手椅型石墨烯纳米带的能带结构.随着弯曲程度的不同,能带带隙将发生微小的改变,呈现先增大后减小的趋势,这为调制石墨烯纳米带的带隙提供了一种潜在的方法.
[1]Peierls R E.Quelques proprietes typiques des corpses solides[J].Ann I H Poincare,1935,5(3):177-222.
[2]Landau L D.Zur theorie der phasenumwandlungen II[J].Phys Z Sowjetunion,1937,11:26-35.
[3]Landau L D,Lifshitz E M.Statistical Physics[M].Oxford:Pergamon,1980.
[4]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-668.
[5]Ferrari A C,Meyer J C,Scardaci V,et al.Raman spectrum of graphene and graphene Layers[J].Phys Rev Lett,2006,97(18):187401.
[6]Saito R,Gdresselhaus G,Gdresselhaus M S.Physical properties of carbon nanotubes[M].London:Imperial College Press,2003:1-33.
[7]Sadowski M L,Martinez G,Potemski M.Landau level spectroscopy of ultrathin graphite layers[J].Phys Rev Lett,2006,97(26):266450.
[8]Zhang Yuanbo,Tan Yanwen,Stormer H L,et al.Experimental observation of the quantum Hall effect and Berry′s phase in graphene[J].Nature,2005,438(7065):201-204.
[9]Katsnelson M I,Novoselov K S,Geim A K.Chiral tunneling and the klein paradox in graphene[J].Nature Physics,2006,2(9):620-625.
[10]Nakada K,Fujita M,Dresselhaus G,et al.Edge state in graphene ribbons:Nanometer size effect and edge shape dependence[J].Phys Rev B,1996,54(24):17954-17961.
[11]Wakabayashi K,Fujita M,Ajiki H,et al.Electronic and magnetic properties of nanographite ribbons[J].Phys Rev B,1999,59(12):8271-8282.
[12]Sasaki K,Murakami S,Saito R.Stabilization mechanism of edge states in graphene[J].Appl Phys Lett,2006,88(11):113110-113112.
[13]Brey L,Fertig H A.Electronic states of graphene nanoribbons studied with the Dirac equation[J].Phys Rev B,2006,73(23):235411-235445.
[14]Shenoy V B,Reddy C D,Ramasubramaniam A,et al.Edge-stress-induced warping of graphene sheets and nanoribbons[J].Phys Rev Lett,2008,101(24):245501-245505.
[15]Huertas-Hernando D,Guinea F,Brataas A.Spin-orbit coupling in curved graphene,fullerenes,nanotubes,and nanotube caps[J].Phys Rev B,2006,74(15):155426.
[16]Cortijo A,Vozmediano M A H.Electronic properties of curved graphene sheets[J].Europhys Lett,2007,77(4):47002.
[17]Reich S,Maultzsch J,Thomsen C,et al.Tight-binding description of graphene[J].Phys Rev B,2002,66(3):35412-35412.
[18]Zheng Huaixiu,Wang Z F,Luo Tao,et al.Analytical study of electronic structure in armchair graphene nanoribbons[J].Phys Rev B,2007,75(16):165414-165419.
[19]Kleiner A,Eggert S.Curvature,hybridization,and STM images of carbon nanotubes[J].Phys Rev B,2001,64(11):113402-113405.
(责任编辑 杜利民)
Effectofbendingontheelectronicpropertiesofarmchairgraphenenanoribbons
HUANG Qiong, TONG Guoping
(InstituteofCondensedMatterPhysics,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
Graphene sheet had a quasi-planar structure which was not totally flat. To simulate the effect of non-flat by using the tight-binding method and orbital hybridization theory, it was studied the armchair graphene nanoribbons(A-GNRS) with bending.The results showed that the bending A-GNRS energy spectra was obviously depend on the curvature, and with certain width, the gap of energy band increased with increase of curvature of the bending A-GNRS.
tight-binding; non-flat; graphene nanoribbons; band structure
O481.1
A
1001-5051(2013)01-0083-05
2012-03-23
黄 琼(1986-),男,浙江绍兴人,硕士研究生.研究方向:低维凝聚态理论.
童国平.E-mail: tgp6463@zjnu.cn

