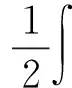一类带有Hardy项和Sobolev-Hardy临界指数椭圆方程的非平凡解*
刘 震, 沈自飞
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
一类带有Hardy项和Sobolev-Hardy临界指数椭圆方程的非平凡解*
刘 震, 沈自飞
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
研究了一类带有Hardy项和Sobolev-Hardy临界指数的椭圆方程
通过运用变分方法和精确估计得到了非平凡解u∈D1,2(Ω)的存在性.其中:Ω⊂RN(N≥3)是一个有界光滑区域,0∈Ω,λ>0,μ∈R,0≤s<2.
Hardy不等式;Sobolev-Hardy临界指数;变分方法;非平凡解
0 引 言
近年来,许多学者考虑了方程
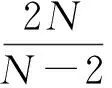

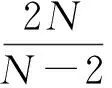
本文考虑以下方程:
式(4)中:Ω⊂RN(N≥3)是包含原点的有界光滑区域;λ为正参数;0≤s<2;μ∈R.因为当Ω是一个星型区域时,由Pohozaev等式可知,若q=2*,则方程(4)无非平凡解,故这里只考虑2 其中D1,2(Ω)={u∈L2*(Ω):|▽u|∈L2(Ω)},通过定义最佳Sobolev-Hardy常数 并找到了方程 的径向对称基态解 满足 式(7)中 类似于Aμ,s的定义,在空间D1,2(Ω)上定义常数 以下是本文的主要结果: (h0)h(x)∈C(Ω)∩L∞(Ω); 首先,给出关于Hardy不等式和Sobolev-Hardy不等式的2个引理,它们将在定理的证明中起到很好的作用. 为了用变分方法解决问题(4),在D1,2(Ω)上定义方程(4)的能量泛函为 由引理1和引理2知,I(u)有定义且I∈C1(D1,2(Ω),R).一般地,称u∈D1,2(Ω)是问题(4)的一个弱解,如果对任意的φ∈D1,2(Ω),有 因此,方程(4)的弱解就是能量泛函I在D1,2(Ω)上的临界点. 接下来通过山路引理证明I满足局部Palais-Smale条件(简记(PS)c),从而得到I在D1,2(Ω)中的临界点,即方程(4)的弱解. 引理3假设条件(h0),(h1)成立,且0≤s<2,2 证明 根据 由引理1可知, 由Sobolev-Hardy不等式可得 ‖u‖2*(s). (14) 因为2 (15) 引理4当0≤s<2,λ>0,2 (17) (18) 由Sobolev-Hardy不等式知,存在C3>0,使得 由Hardy不等式得 从而 接下来证明I在D1,2(Ω)中满足局部(PS)c条件. 证明 由引理3和引理4知I存在(PS)序列{un},且{un}在D1,2(Ω)中有界,从而存在一个收敛子列,不妨仍记为{un},当n→∞时,有 令υn=un-u,则由Brezis-Lieb引理[11]及Vitali′s定理有 由式(27)可令 (29) 接下来考虑函数: 由λ,tε>0可知, 从而得到 t0ε. (38) 结合式(30)与式(31)得 进一步,根据条件(h2)有 (40) 引理6证毕. 证明 由引理1~引理6即可证得定理1. 注1为了得到正解的存在性,可以在D1,2(Ω)中考虑 其中,u+:=max{u,0}.从而,I+∈C1(D1,2(Ω),R),且I+的临界点即为方程(4)的正解. [1]Brezis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents[J].Comm Pure Appl Math,1983,36(4):437-477. [2]Ferrero A,Gazzola F.Existence of solutions for singular critical growth semilinear elliptic equations[J].J Differential Equations,2001,177(2):494-522. [3]Cao Daomin,Peng Shuangjie.A note on the sign-changing solutions to elliptic problems with critical Sobolev and Hardy terms[J].J Differential Equations,2003,193(2):424-434. [4]Ghoussoub N,Yuan C.Multiple solutions for quasilinear PDEs involving the critical Sobolev and Hardy exponents[J].Amer Math Soc,2000,352(12):5703-5743. [5]沈自飞,杨敏波.具 Hardy-Sobolev临界指数椭圆方程的非平凡解[J].数学学报,2005,48(5):999-1010. [6]Kang Dongsheng,Peng Shuangjie.Positive solutions for singular crtical elliptic problems[J].Appl Math Letters,2004,17(4):411-416. [7]康东升.一种奇异临界椭圆方程的非平凡解[J].数学物理学报,2006,26A(5):716-720. [8]Adimurthi,Filippas S,Tertikas A.On the best constant of Hardy-Sobolev Inequalities[J].Nonlinear Analysis,2009,70(8):2826-2833. [9]García Azorero J P,Peral Alonso I.Hardy inequalities and some critical elliptic and parabolic problems[J].J Differential Equations,1998,144(2):441-476. [10]Ambrosetti A,Rabinowitz P H.Dual variational methods in critical point theory and applications[J].J Functional Analysis,1973,14(4):349-381. [11]Brezis H,Lieb E.A relation between pointwise convergence of functions and convergence of integrals[J].Proc Amer Math Soc,1983,88(3):486-490. [12]Han Pigong.Quasilinear elliptic problems with critical exponents and Hardy terms[J].Nonlinear Analysis,2005,61(5):735-758. (责任编辑 陶立方) ExistenceofnontrivialsolutionsforaclassofellipticequationsinvolvingHardytermsandSobolev-Hardycriticalexponents LIU Zhen, SHEN Zifei (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China) It was discussed a class of elliptic equations involving Hardy terms and Sobolev-Hardy critical exponents The existence of nontrivial solutions was proved via variational methods and delicate estimates, whereΩ⊂RN(N≥3) was an bounded domain with smooth boundary and containing the origin 0,λ>0,μ∈R, 0≤s<2. Hardy inequality; Sobolev-Hardy critical exponents; variational methods; nontrivial solutions O175.25 A 1001-5051(2013)01-0045-09 2012-09-02 国家自然科学基金资助项目(10971194;11101374) 刘 震(1986-),男,浙江龙游人,硕士研究生.研究方向:非线性泛函分析.

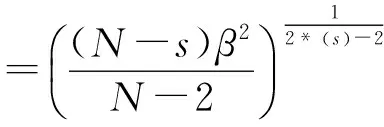





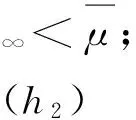

1 引 理



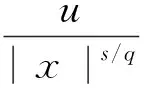

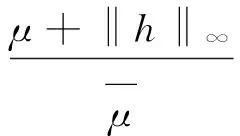
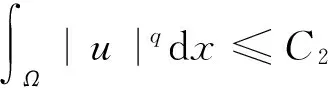
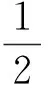
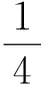
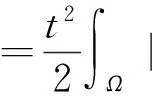


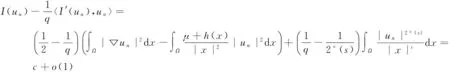

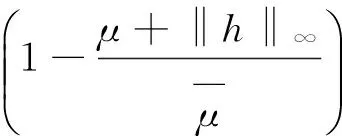
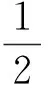
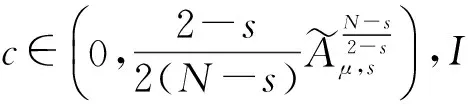





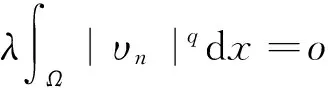




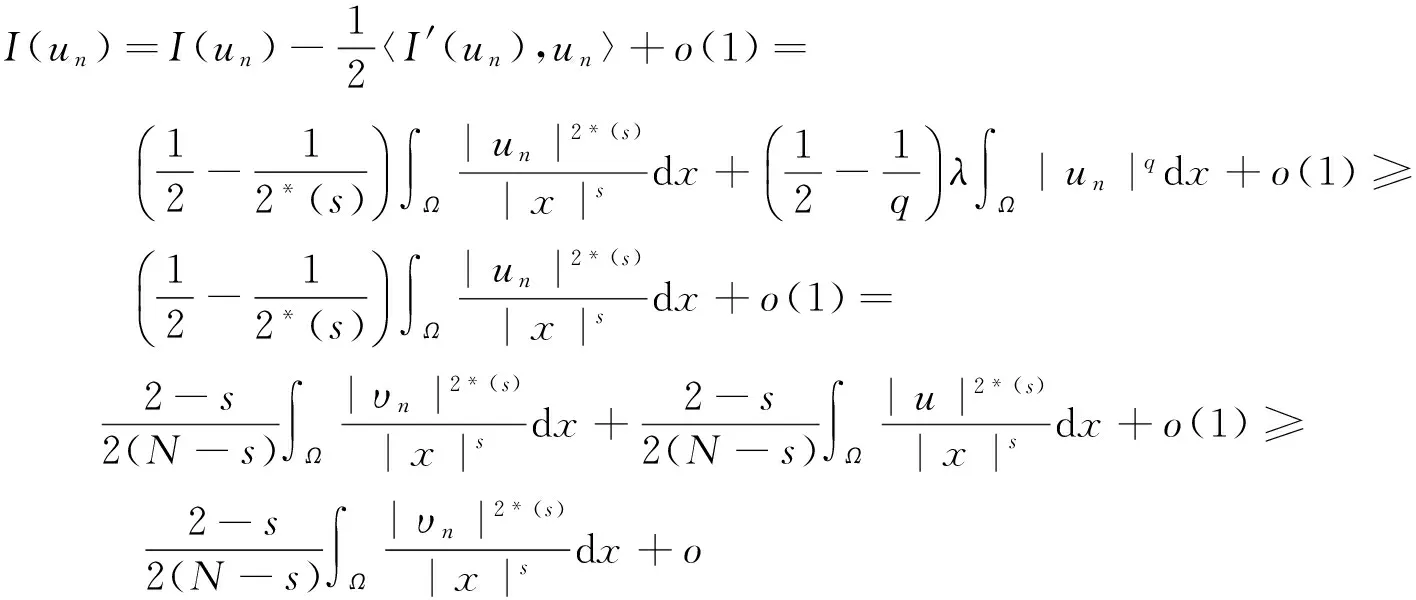

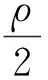



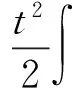









2 定理1的证明