Maxwell-Bloch 方程的Hopf分叉研究*

汪灵杰, 赵晓华

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

Maxwell-Bloch 方程的Hopf分叉研究*

汪灵杰, 赵晓华

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

主要考虑了基于Maxwell-Bloch方程激光模型的动力学行为，分析了Maxwell-Bloch方程的平衡点稳定性和Hopf分叉行为，给出了相应的数值模拟及分叉图.

Maxwell-Bloch方程;中心流形;Hopf分叉;数值模拟

0 引 言

所谓Maxwell-Bloch方程(M-B系统),是指下面的常微分方程组:

式(1)中:E为缓变包络场强;P是指原子的极化强度;Δ是指粒子数反转;k为场强;γ⊥为原子极化;γ‖为粒子的损失率;g为耦合常数;Δ0为无耦合情况下的粒子数反转;k,γ⊥,γ‖,g,Δ0,均取正值.对于本文讨论的腔模频率与原子频率处于共振情况,E和P均是实变量,这样M-B方程组就变成一个3维自洽微分方程组.关于Maxwell-Bloch方程的推导及背景,可参考俄罗斯学者Ya I Khanin的专著《Fundamentals of Laser Dynamics》(2006).

注意到,当参数满足关系k=σ,γ⊥=g2/k=1,g2Δ0/k=r,γ‖=b,而记x=E,y=gP/k,z=Δ0-Δ时,方程(1)就是著名的Lorenz方程.因此,Maxwell-Bloch方程(1)以Lorenz方程为其特例.

近几年来，在激光动力学领域里，人们对M-B激光方程从不同层面作了些理论分析和实验研究[1-4],展现了其丰富的非线性动力学行为,如分叉、混沌等.Bloch方程是一个与Schrödinger方程类似的方程,用来描述共振耦合激光场原子的演变过程,而Maxwell方程则描述了光场在介质中的传播特性.2个方程耦合在一起,造就了更加复杂的动力学行为.

1 平衡点分叉及稳定性分析

由于系统(1)包含有5个非零参量,为便于研究,将通过尺度变换以减少参量个数.为此,引入变换

则系统(1)转化为本文要讨论的三参数系统形式

1.1平衡点A的稳定性分析

系统(3)在平衡点A处对应线性系统的Jacobi矩阵为

其对应的特征方程为f(λ)=(λ+1)[(λ+η1)(λ+η2)-η3],相应的特征根为

从式(4)可得以下定理:

定理11)若η1η2-η3>0,则特征根全为负实数，平衡点A为稳定结点类型;

2)若η1η2-η3<0,则特征根为一正两负实数，平衡点A为鞍型不稳定;

3)若η1η2-η3=0,则特征根为λ1=0,λ2=-(η1+η2)<0,λ3=-1<0,平衡点A是不稳定的.

证明 前2个结论显然,以下证明结论3).由特征值可知,此时平衡点属于退化临界情形,满足中心流形定理的条件,故用中心流形理论[5]进行处理.

先把平衡点A平移到原点,令x=X,y=Y,z=Z+η3,则系统(3)变为

再对系统(5)作如下变换:

则系统(5)变为

即

.

此时,可设式(6)的局部中心流形为

式(7)中,h1,h2满足

h1(0)=h2(0)=h′1(0)=h′2(0)=0.

将式(7)代入式(6),得到关于h1(Y1),h2(Y1)的微分方程组

将h1(Y1),h2(Y1)展开成级数形式,即

将式(9)代入式(8),比较两端同次幂的系数可得

从而中心流形有近似表示

将中心流形式(10)代入式(6),可得中心流形上的方程为

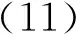
则由式(11)及η1(η1+η2)>0可知,中心流形上的平衡点Y1=0是不稳定的.故可知在参数满足η3=η1η2的条件下,整个系统平衡点A是不稳定的.定理1证毕.

1.2平衡点B和C的稳定性分析

系统(3)在平衡点B和C处对应线性系统的Jacobi矩阵为

对应的特征多项式均为

分析特征方程(12)的根可得如下定理：

定理2对于任意的η1>0,η2>0,η3>η1η2,

证明 利用Hurwitz定理,写出H矩阵为

从而,式(12)的特征值的实部全为负数的充要条件是矩阵H的所有顺序主子式全为正数,即

由于η1>0,η2>0,η3>η1η2,所以只要证明D2>0即可.再对D2>0进行简单分析即可得定理2的结论.

2 平衡点B和C附近的Hopf分叉分析

将η3=η*3代入平衡点B和C处的特征方程(12),得

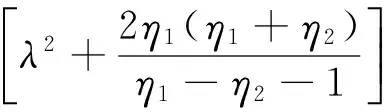
因此,特征根为一对纯虚根和一个负实根,即

由于特征方程(12)的系数连续依赖于参数η3,特征值也连续依赖于η3,因此,对满足条件η1>1+η2的任意取定的(η1,η2),只要η3充分接近η*3,特征方程(12)的特征值必为

且

将式(15)中的特征值形式代入特征方程(12),整理得

注意α是η3的函数,在式(17)中固定η1,η2,两端关于η3在η3=η*3处求导数(注意α(η*3)=0),得

至此,已证明了系统(3)在平衡点B和平衡点C处的特征值满足式(16)和式(18),即满足Hopf分叉定理[6-7]的条件.从而得出下面的定理：

接下来利用文献[7]中的方法进一步分析Hopf分叉周期解的分叉方向和稳定性.为此,以下约定正参数η1和η2是满足条件η1>η2+1的固定常数,将η3视为分叉参数.

J(B)x+S(x).

使得系统(19)在这个变换下变为

式(21)中

由于特征值满足式(16),因此不难求得,在η3=η*3处,

其逆矩阵为

.

其中:d为矩阵P(η*3)的行列式;ω0由式(14)定义.若记式(21)中的非线性项为

P-1(η3)S(P(η3)u)F(u,η3)=(F1,F2,F3)T,(24)

则代入Hopf分叉临界参数值η3=η*3,可得F(u,η*3)的分量为:

利用F(u,η*3)的分量表示可很方便地计算出下面的偏导数：

Fkij(0,η*3),Fkijl(0,η*3).

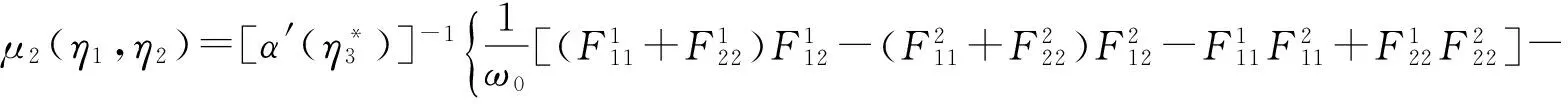
(25)

μ2(η1,η2)的表达式很长,无法直接分析,但利用Maple数学软件就能很容易通过数值模拟得出断言：对满足条件η1>η2+1的η1和η2的任何正值,函数μ2(η1,η2) 恒小于零.

对平衡点C也可作类似的分析,并且可得与平衡点B完全相同的结论.于是,结合式(18),并根据文献[7-8],立即可得下面的定理：

为了说明上述Hopf分叉周期解的分叉方向和稳定性,给出如下一个实例:取η1=4,η2=1,η3作为自由参数,此时,η*3=64,平衡点B(3.872 983 346,15.491 933 38,4),且

因此,当η3接近并小于η*3=64时,在平衡点B附近存在一个不稳定的周期解,这是因为

μ2α′(η*3)=-0.124 006 408 7<0.

3 数值模拟

下面展现一些数值模拟结果,验证Hopf分叉周期解的存在性.在此，以η3作为分叉参数，且所有的分叉图都是用Matcont软件[9]画出来的.

图1、图2分别是以x,y作为状态变量，η3作为分叉参数的M-B方程平衡曲线及其分叉图.

图1 变量x关于η3的分叉图

图2 变量y关于η3的分叉图

从图3可以看到:当分叉参数η3=64时,存在2个对称的Hopf分叉点H，并且其第一Lyapunov系数为0.000 394 074 4,说明是亚临界Hopf分叉;当分叉参数η3=4时，存在1个BP点,即平衡点A.图4是以正的Hopf分叉点H作延拓计算而得到的极限环分叉图，因为Hopf分叉点的存在，意味着极限环的存在，故在对其进行延拓计算时只需寻找余维数1上的极限环分叉.图4仍以η3作为自由参数，得到的是以状态变量x为极限环的振幅随参数η3的分叉图.随着参数η3的变化，很快就得到环极限点(LPC),但当参数η3继续变小时，极限环的振幅进一步增大.图5为平衡点分叉与Hopf分叉合成图.从图5可以看出:当η3<η1η2时,该系统只有1个不稳定的平衡点;当η3>η1η2时,该系统有3个平衡点;当η3=η*3时,存在2个Hopf分叉点,此时,系统在Hopf分叉点附近产生2个亚临界的Hopf分叉周期解.

图3 图1和图2的数据截图

图4 Hopf分叉点H的延拓分叉图

图5 平衡点分叉与Hopf分叉合成图

以上数值模拟结果验证了本文理论分析的可靠性,同时M-B方程还具有其他方面更复杂的动力学行为，如广义Hamilton扰动系统的周期轨道、同宿轨道分支与混沌[10]等运动.对此,笔者将作进一步的研究.

[1]Arecchi F T,Lippi G L,Puccioni G P,et al.Deterministic chaos in lasers with injected signal[J].Opt Commun,1984,51(5):308-314.

[2]Arecchi F T.Chaos and generalized multistability in quantum optics[J].Phys Scr,1985,T9:85-92

[3]Arecchi F T,Boccaletti S,Ramazza P.Pattern formation and competition in nonlinear optics[J].Physics Reports,1999,318(1/2):1-83.

[4]Hacinliyan A S,Kusbeyzi I,Aybar O O.Approximate solutions of Maxwell Bloch equations and possible Lotka Volterra type behavior[J].Nonlinear Dynamics,2010,62(1/2):17-26.

[5]Wiggins S.Introduction to applied nolinear dynamical systems and chaos[M].2nd ed.New York:Springer,2003:245-265.

[6]Hassard B,Kazarinoff N,Wan Y.Theory and application of Hopf bifurcation[M].Cambridge:Cambridge University Press,1981.

[7]Hsü I D,Kazarinoff N D.An applicable Hopf bifurcation formula and instability of small periodic solutions of the Field-Noyes model[J].J Math Anal Appl,1976,55:61-89.

[8]Hsü I D,Kazarinoff N D.Existence and stability of periodic solutions of a third-order nonlinear autonomous system simulating immune response in animals[J].Proc Roy Soc Edinburgh Sect:A Mathematics,1977,77(1/2):163-175.

[9]Dhooge A,Govaerts W,Kuznetsov Y A,et al.MATCONT and CL_MATCONT: Continuation toolboxes in matlab[M].The Netherlands:Utrecht Universities Press,2006.

[10]李继彬,赵晓华,刘正荣.广义哈密顿系统理论及其应用[M].北京:科学出版社,2007:123-152.

(责任编辑 陶立方)

StudyonHopfbifurcationforMaxwell-Blochequation

WANG Lingjie, ZHAO Xiaohua

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The dynamic behavior of the laser model: the Maxwell-Bloch equations was studied. Stability of equilibrium, Hopf bifurcation behavior in this system were investigated in detail and the associated numerical simulation and bifurcation diagrams were also presented.

Maxwell-Bloch equation; center manifold; Hopf bifurcation; numerical simulation

O175.14

A

1001-5051(2013)01-0037-08

2012-10-23

国家自然科学基金资助项目(10872183;11172269)

汪灵杰(1984-),男,浙江临海人,硕士研究生.研究方向：微分方程与动力系统.

赵晓华. E-mail: xhzhao@zjnu.cn