混合流优先控制T 型交叉口通行能力研究
陈吉发,李文权
(1.深圳市综合交通设计研究院,广东 深圳 518003;2.东南大学,江苏 南京 210096)
道路通行能力是指在特定的道路条件、交通条件和人为的度量标准下,单位时间内能够通过的最大交通量。在城市道路网规划与评价、交叉口规划与设计以及道路工程研究等多项工作中,道路通行能力都是最基本的定量依据指标。具体来说,城市道路是由路段和交叉口组成,相对于路段而言,道路交叉口由于不同交通流的转向而引发相互间的冲突、交汇、分流等运行行为,交通特性较为复杂,尤其是在我国城市中占较大比例的无信号控制交叉口,由于缺乏严格的管理控制方式,往往成为城市道路网中通行能力的“隘路”和交通事故的“多发源”,其通行能力直接影响着整个城市道路网的通过能力。因此,城市无信号控制交叉口(以优先控制交叉口为主)通行能力也一直是城市道路通行能力研究的重点和热点。
目前,国内外研究无信号(优先控制)交叉口的理论通行能力模型,基本可以分为两类:基于回归技术的实测模型和基于概率论的可接受间隙理论模型。由于实测模型的应用局限性较大,难于推广。近年来,可接受间隙理论模型的发展较快,许多学 者 如TROUTBECK(1986,1991)、COWAN(1987)、常玉林、王炜等,通过改进主路交通流车头时距的分布函数,进而得到了许多不同的理论模型,但这些成果都是将支路车流假设为单一车型的理想车流,与我国实际情况相差较大。李文权、王炜等,针对我国城市道路的混合交通流特性,建立无信号交叉口多车型混合车流的通行能力模型,取得较大进展。但仍需要指出的是,在我国大多数城市优先控制交叉口,存在着大量的行人和非机动车流,与车流运行冲突,对交叉口通行能力产生显著影响。因此,如何评估上述影响,建立适合我国混合流条件下的无信号(优先控制方式,且行人及非机动车流量较大)交叉口通行能力模型是十分紧迫的问题。
1 混合流交通特性分析
城市优先控制T 型交叉口是由两条道路相交而成,其中流量较大的称为主路或干路,而流量较小的(多为断头路)则称为支路或次路。该类交叉口是无信号控制与有信号控制之间的一种过渡形式,通常在支路入口处设置让行或停车标志,遵循主路优先通行的原则,支路车辆必须让主路车辆先行。
混合交通流是我国城市道路交通的重要特性,在交叉口处,除机动车流外,还存在大量的行人与非机动车流,各类交通流相互干扰,对通行能力影响大。根据实地勘测,在城市优先控制T 型交叉口处,行人及非机动车流区别于机动车流,具有速度慢、稳定性差、集群性以及灵活性等特点,其中以集群性最为突出。若以道路某一横断面为参考面,非机动车个体之间存在明显的叠加现象。与此同时,行人流过街行进过程中,一般也不严格按照有规律的纵向队列前进,而是在人行横道范围内“随意”行走,因而“成群前进”现象较为普遍。
参考相关文献成果,在研究行人及非机动车流的到达特性时,通常以“群”为单位进行分析。以非机动车流为例来定义“群”,首先定义一个空隙的概念,以道路某一断面为参考界面,在某段时间内该断面没有非机动车通过,将这段没有非机动车通过的时间段称为非机动车流中的一个空隙,如图1所示。
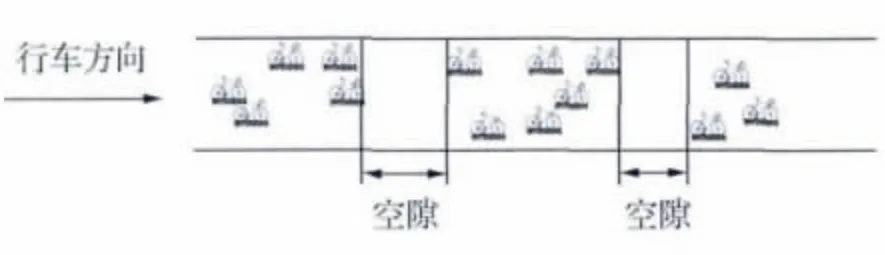
图1 非机动车流中空隙示意
任意两个相邻空隙间的非机动车定义为一群,本文假定当到达交叉口处的非机动车前后时差不超过tpb(tpb为前后到达的非机动车群的最小空隙值)时,则该部分非机动车被算作同一群;如果单辆非机动车到达交叉口处的时间差大于tpb,则单辆非机动车也算一群。tpb取值大小与到达交叉口的非机动车流量以及交叉口的实际运行状况密切相关。
2 混合流优先控制T 型交叉口通行能力研究
2.1 混合交通流运行优先等级划分
依据《HCM2000》中对不同交通流运行优先等级的划分规则,并结合大量的实地调研观测,本文将该类交叉口到达的行人及非机动车流(按照“群”为单位统计)看作独立的冲突流,对交叉口混合交通流的运行优先等级详细划分,共包括“Ⅰ-Ⅴ”5级,其中Ⅰ级交通流运行优先等级最高,通过交叉口时具有绝对优先权,不需让行其他交通流;“Ⅱ-Ⅴ”级交通流等级依次降低,在通过交叉口时需让行等级较高的交通流,具体见表1。

表1 交叉口内不同交通流运行优先等级划分
2.2 次级交通流通行能力模型
根据相关研究文献,在穿越交叉口主路多重优先独立冲突流的情形下,支路次级交通流k的通行能力计算模型

结合实地调研发现,对应不同的优先冲突交通流,次级交通流选择穿越的临界间隙及随车时距值发生变化。例如,对支路次级交通流而言,相较于距离较远的主路机动车流,其选择穿越较近的行人及非机动车流的临界间隙值明显偏小。因此,为提高通行能力计算的实用性和准确性,应基于上述计算模型,进一步细分行人及非机动车流、机动车流,设置相应的临界间隙和随车时距值。
考虑我国城市优先控制交叉口主路机动车流车头时距主要服从移位负指数和M3分布,同时将交叉口内行人及非机动车流看作独立的优先冲突流,其到达时距验证主要服从移位负指数分布。
1)主路优先冲突流车头时距均服从移位负指数分布,次级交通流通行能力算式

上述通行能力计算模型可转化为
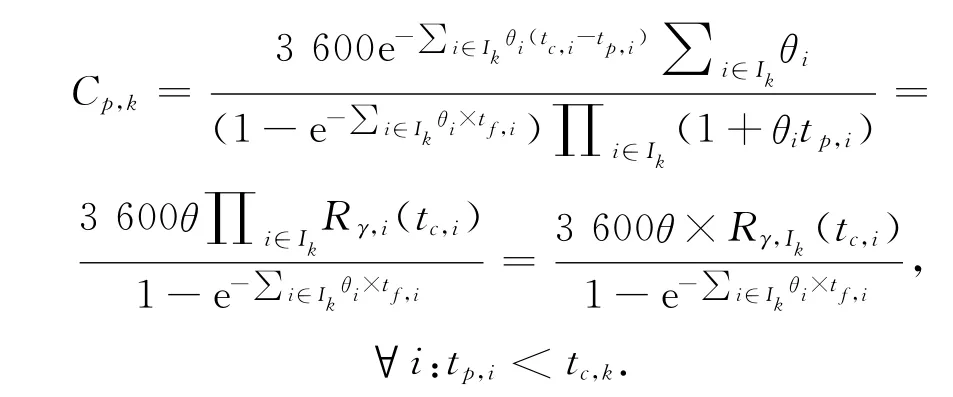
其中,R(t)车头时距分布的残存函数(survivor function);tc,i,tf,i为临界间隙和随车时距,s;θ=,tp,i为最小空隙值。
2)当主路优先冲突流车头时距服从不同分布时,即机动车流服从M3分布,而行人与非机动车群到达空隙服从移位负指数分布,则次级交通流通行能力算式

其中,qj为主路车道j的交通流率(pcu/h);φi是指组成过程i中自由流的概率;而γi=qi×φi/(1-qiΔi),对应过程i的衰减常量;其他参数意义同上。
2.3 通行能力模型验证
选取调研的T2×2型(横过支路行人流400 人/h,主路直行非机动车439辆/h)、T2×4型(横过支路行人流126人/h,主路直行非机动车653辆/h)交叉口的支路次级交通流通行能力对上述模型进行验证,结果如表2和表3所示。

表2 T2×2型交叉口次级交通流通行能力

表3 T2×4型交叉口次级交通流通行能力
比较结果可得,本文修正模型是较经典的间隙接受理论模型,误差相对较小,更切合于我国优先控制交叉口的实际情况。
3 结束语
在开展大量实地调查的基础上,分析交叉口混合交通流特性,借鉴经典的间隙接受理论模型,将主路到达的行人及非机动车流看作是独立的优先冲突流,并对交叉口内混合交通流的运行优先等级进行划分,对各级交通流间的冲突特性进行分析,最终建立适应我国混合流下优先控制T 型交叉口的通行能力计算模型,最后通过算例对模型的准确性进行验证。
[1]TROUTBECT R J.Average delay at an unsignalized intersection with two major stream each having a dichotmized headway distribution[J].Transportation Science.1986,20(4):272-286.
[2]COWAN R J.An extension of Tanner reaults on uncontrolled intersection:clarification of some issues[J].Queueing System,1987,(1):249-263.
[3]常玉林,王炜.主路车流服从Erlang分支路通行能力研究[J].东南大学学报,1998,98-102.
[4]王炜,李文权.无信号交叉口多车型混合车流的通行能力[J].中国公路学报,2000,13(2):83-87.
[5]梁春岩.自行车交通流特性及其应用研究[D].长春:吉林大学,2007.
[6]Hagring O.A further generalization of Tanner,s formula[J].Transportation Research,1998,32(6):423-429.
[7]詹晓松.城市信号交叉口行人过街速率分析[J].交通科技与经济,2012,14(5):73-76.
[8]张威,刘琦.城市道路T 型交叉口咬通改善设计[J].交通科技与经济,2010,12(3):16-18.

