点云数据配准算法的研究

于明旭，纪志浩，林乐胜

（1.江苏建筑职业技术学院，江苏 徐州 22116；2.中国煤炭地质总局普查队，江苏 徐州 22116）

1 点云数据配准原理

点云配准实质是刚体变换。是通过平移矩阵T和旋转矩阵R对一组点云数据进行变化，平移矩阵T和旋转矩阵R如下式

式中：tx，ty，tz为位移量；α，β，γ为x，y，z轴旋转角。

使用刚体变换将不同视角下特征点集A＝｛ai｝，B＝｛bi｝，i＝1，2，3，…，k匹配到一起，需求解出平移矩阵T和旋转矩阵R，实质是求解目标函数的值最小。目标函数选取方法多为欧氏距离以及欧氏距离的变形，其公式为

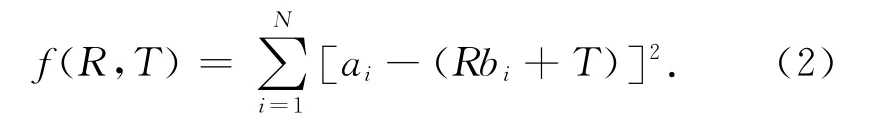
点云数据配准主要涉及以下几个坐标系：扫描仪坐标系 （SOCS）；仪器自身局部坐标系，获取原始点云数据是以该坐标系为参考；项目坐标系（PRCS），该坐标系统是由用户定义的一种局部坐标系；全局坐标系 （GLCS），定义为包含项目坐标系的一种坐标系统，与项目坐标系相比该坐标系包含数据量较大。各种坐标关系如图1所示，在图1中扫描场景是一个矩形建筑物的俯视图，项目坐标系用Xpr、Ypr、Zpr表示，属于右手坐标系，Ypr平行于建筑物边，项目坐标系的原点与矩形建筑物的拐角重合。全局坐标系是左手坐标系，在图中用Xgl、Ygl、Zgl表示。用Xspi、Yspi、Zspi（i＝1，2，3，…，N）表示不同站点的扫描仪坐标系。

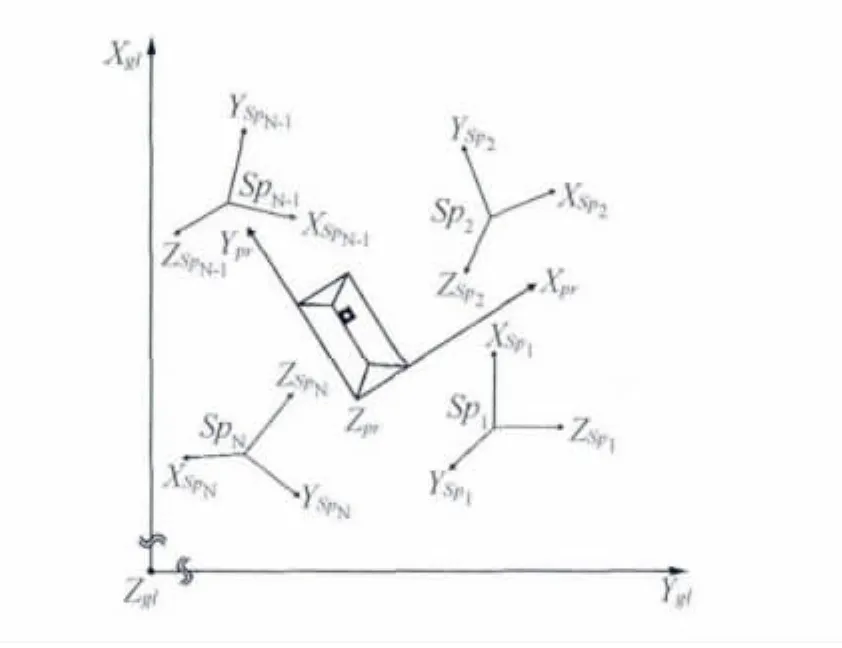
图1 各种坐标系关系

点云数据配准过程，实质就是将各站基于扫描仪坐标系获得的点云数据转换到项目坐标系或全局坐标系。转换关系如图2所示。

图2 数据配准过程

2 配准误差解算

本文采用两站中同名点点对配准或距离中误差σ0作为评价两站点云配准精度指标，中误差σ0的计算式子为

式中：（xi，yi，zi）为目标点集中目标点的坐标；（x′i，y′i，z′i）为转入目标点集中点的坐标；n为控制点个数；k为配准时未知数个数，值为7。

3 配准方法

粗配准即初始配准，是概略算出点云之间旋转矩阵和平移向量。本文使用有反射标志同名点提取方法。这种办法采用人机交互，解决了准确确定同名点问题时，耗时较长的问题。反射体有圆柱形、扁平圆形和球形，如图3所示。

图3 反射体

在扫描前将反射体粘贴在被扫描物体周围，在扫描过程中反射体固定不动，利用相同的反射体在不同扫描站中的位置关系对不同的扫描站间点云数据进行配准，为了解计算MSOP，需至少已知不共线的3个反射体在2个坐标系下的坐标值，为削弱配准误差，在实验中应用4个反射体。基于反射标志同名点配准所使用的公共反射体坐标，如表1所示。

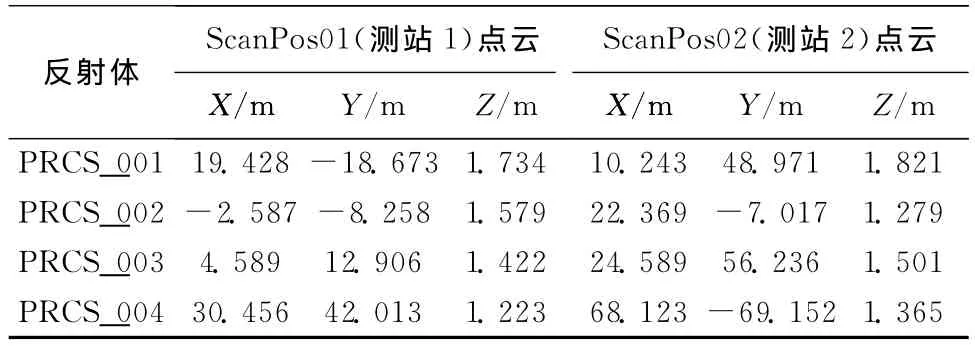
表1 相邻两站公共反射体信息表

两站点共有4个共同反射体坐标，其应用式旋转矩阵为

平移向量为

式（1）计算得到旋转角为：（α）Roll为2.207°；（β）Pitch为0.826°；（γ）Yaw为－136.183°。根据式（3）得到标准偏差值为0.053m，可以为精配准算法提供初始位姿。

4 精配准

4.1 算法原理

精配准是在粗配准基础上提高点云之间配准精度，实验时选择的同名点对应该大于3对，通过最小二乘原理求解R和T最优解，本文使用间接平差，即通过列出误差方程求解点云配准表达式（4），式（4）中参数为（x0，y0，z0，u，α，β，γ），用级数展开至一次项可得到线性转换模型的误差方程式（5），其系数矩阵为式（6），li为式（7），¯x为式（8）。

由间接平差可得

式中：p为权值，取单位矩阵；Vi为第i个同名点配准后的误差；x′iy′iz′i为已经配准点云集坐标系o′－x′y′z′下坐标；xyz为未配准坐标系o－xyz中的点云数据，由o－xyz向o′－x′y′z′坐标系配准。

设pi、qi分别属于o－xyz和o′－x′y′z′坐标系，（pi，qi）为同名点，i取3。令

然后对正交向量vi，wi正交单位化，得

将[v]中的数据集V变换到[w]，变换关系为V′＝RV＋T，利用正交关系得到上述的R与T，则R＝[v]－1·[w]，t＝p1[v]－1·[w]＋q1。

4.2 算法描述

第一步：基于同名点进行粗配准；

第二步：粗配准结果α，β，γ，u，x0，y0，z0作为算法的初始位姿；

第三步：每次计算得到的α，β，γ，u，x0，y0，z0作为下次迭代运算的初始值；

第四步：重复二、三两步；

第五步：当两次迭代结果之差小于10－6，停止迭代。

在C＋＋中实现算法，以化石数据为例，两站点云数据配准过程如图4所示，其中a为配准前数据，b为配准后的数据。根据（2）式得标准偏差为0.0057m，平移旋转矩阵如下式

图4 配准前后效果

5 结束语

本文将点云数据配准分两步进行，先采用人机交互的方法进行粗配准，在粗配准的基础上，应用最小二乘间接平差理论，通过算法实现精确配准，并以两站中同名点的点对配准后距离误差作为配准精度的衡量指标。实验表明，此方法的优点是基于同名点配准方法简单，效率高，可以为精确配准算法提供初始位姿，降低数据配准耗时，同时，也避免精配准数据因局部收敛出现的病态状况。通过实验验证此方法配准后的数据能满足后续使用要求。

[1] D FAUGERAS，M HEBERT.The representation，recognition，and locating of 3dobjects[J].International Journal of Robotic Research，Fall 1999，53（3），27－52.

[2] K S ARUN，T S HUANG，S D BLOSTEIN.Least square fitting of two 3－D point sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1998，9（5）：698－700.

[3] P J BESL，N D MCKAY.A method for registration of 3－D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，14（2），239－256.

[4] 张宗华，彭翔，胡小唐.ICP方法匹配深度图像的实现[J].天津大学学报，2012，35（5）：571－576.

[5] 喜文飞，方源敏，李帅，等.一种新的激光点云数据精简方法[J].测绘工程，2012，21（4）：38－40..

[6] 梁振华，王晨，谢宏全.基于莱卡C10获取校园三维点云数据设计[J].测绘工程，2013，22（1）：47－50.