子午线轮胎驻波临界速度仿真及试验研究
王 强,张 娜,石玉环,齐晓杰,王东浩
(1.黑龙江工程学院 汽车与交通工程学院,黑龙江 哈尔滨 150050;2.黑龙江东方学院 土木建筑工程学部,黑龙江 哈尔滨 150080;3.黑龙江省交通厅,黑龙江 哈尔滨 150001)
1 子午线轮胎驻波发生机理分析
汽车在一般速度行驶时,轮胎与地面接触部分会得到压缩,当轮胎旋转到离开地面的上侧时又会恢复原有形状,胎面从变形到最后恢复原状存在一定的滞后时间,其时间长短与车速、负荷、轮胎温度高低等因素有直接关系。轮胎所受负荷越大,车速越高,轮胎胎面产生的离心力就越大,离心力增大会使胎面反向产生变形,轮胎周而复始地运动、压缩和伸张在不断地交替进行,胎面就会产生波动。当车速很高时,并且胎面的波速与轮胎转速一致时就会发生“驻波”。主要表现为轮胎接地面后部的圆周上出现明显的波浪状变形,并伴随有滚动行驶阻力的急剧增加,轮胎内部温度迅速升高,以致胎冠橡胶层与胎体的帘线层的结构合力被减弱,致使橡胶脱层直至轮胎爆破损坏。众多学者把轮胎“驻波”发生时的车速称为“驻波临界速度”。
许多学者对轮胎驻波现象进行了大量研究,其中庄继德采用弹性基环形梁模型公式对轮胎驻波进行研究分析,具有很大的典型性。此模型是将子午线轮胎模拟为由纵向和径向弹簧支撑的环形梁模型(见图1),在分析过程中考虑了轮胎的径向阻尼参数,但不考虑轮胎纵向刚度和胎冠抗弯刚度,并对参数做了进一步的修改和完善,公式为
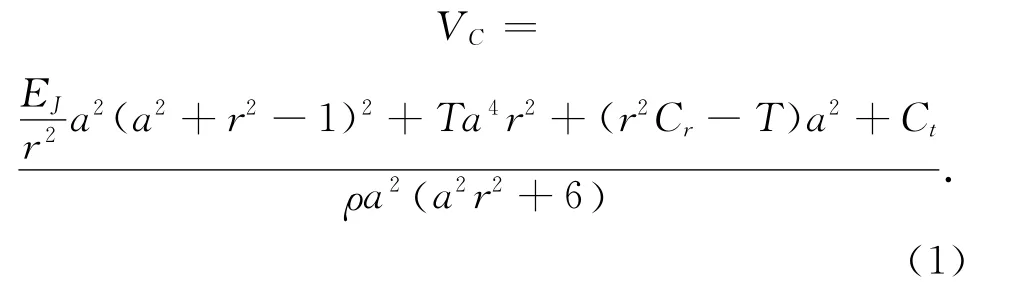
式中:EJ为胎冠的抗弯刚度;r为轮胎外半径;ρ为环行梁单位长度质量;T为带束层的张力;Cr为轮胎单位长径向刚度;Ct为轮胎单位长纵向刚度;a为波数,a=2π/λ(λ为波长)。
对比大量文献资料可以看出庄继德的公式相对较为完整,而且在参数中加入了纵向和横向变形刚度,为此,本文研究参考庄继德的公式做验证和计算。
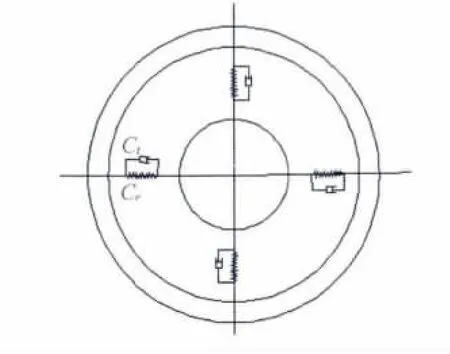
图1 弹性基环形梁模型
2 轮胎驻波临界速度有限元数值模拟
本文应用ABAQUS有限元软件分别模拟了车速为150km/h、160km/h、170km/h、180km/h时的轮胎变形—应力云图,如图2、图3、图4、图5所示,轮胎应变-变形时间结果如图6所示。利用软件及后处理求得轮胎变形恢复时间为0.01311s,驻波临界速度计算公式为


图2150 km/h时变形应力云
3 轮胎驻波临界速度测试及分析
本研究基于高速摄像机技术,并借助底盘测功机及AutoCAD软件分别测试了车速为150km/h、160km/h、170km/h、180km/h时的轮胎变形,其轮胎变形拟合处理曲线如图7、图8、图9、图10所示。


由图中分析可知,当车速分别为150km/h、160km/h、170km/h、180km/h时,拟合函数恢复时间分别为T1=0.0104s、T2=0.0111s、T3=0.0108s、T4=0.0098s,再根据公式

式中:t为标点1以前的恢复时间,tz为总时间,α1为标点1的角度值,αz为最后一点角度值,T为拟合的标点1到最终恢复的时间。
求得T平均=T=0.012516s,r=R-H/3=0.307-0.0097=0.2973m。最终可以求得驻波临界速度为

试验测试结果稍大于仿真结果。
4 结 论
本文在文献资料和测试实验的基础上,确定了一种子午线轮胎临界速度的判定方法,即当高速行驶轮胎变形恢复时间与轮胎转动一周的时间相等时,轮胎将会出现驻波现象,把此时的车速判定为轮胎驻波发生的临界速度。依据该方法,通过高速摄像测试系统测试数据和后期处理得到轮胎的弹性恢复时间,并计算得到195/60R15子午线轮胎在载荷为280kg、充气压力为1.2MPa、环境温度为20℃条件下的驻波临界速度为268.5km/h,此试验测试结果与仿真所得结果符合度较高,稍大于文献资料和实际值。在此基础上分析并得出如下结论:
1)在轮胎载荷不变的情况下,适当提高轮胎的充气压力,可以有效提高轮胎驻波发生的临界速度。
2)在轮胎充气不变的情况下,适当减小轮胎所受的载荷,有利于提高轮胎驻波发生的临界速度。
[1] 庄继德.现代汽车轮胎技术[M].北京:北京理工大学出版社,2001.
[2] 王强,齐晓杰,王云龙,等.高速轮胎驻波临界速度有限元分析[J].车辆动力技术,2011(4):46-50.
[3] 齐晓杰,王强,王云龙,等.子午线轮胎驻波临界速度数值模拟分析[J].黑龙江工程学院学报,2011(4):5-8.
[4] 郝勇,李子然,李大应,等.子午线轮胎驻波现象和临界速度的有限元分析[J].固体力学学报,2007,(9):303-307.
[5] 余治国,李曙林,刘志宏,等.轮胎临界速度影响因素[J].交通运输工程学报,2004(3):111-113.
[6] PADOVAN J.On standing waves in tires [J].Tire-Science and Technology,1997,5(2):25-28.
[7] J R CHOA,K W KIMB,H S JEONGB.Numerical investigation of tire standing wave using 3-D patterned tire model[J].Science Direct,2007(6):126-128.
[8] ANINDA CHATTERJEE,JOSEPH P CUSUMANO,JOHN D ZOLOCK.On contact-induced standing waves in rotating tires:experiment and theory[J].Journal of Sound and Vibration,1999(5):254-256.
[9] 王强,齐晓杰,张娜,等.基于Pro/E与 ANSYS载重车辆轮胎有限元分析[J].交通科技与经济,2009(1):35-38.

