腐蚀作用下多龄期铸铁管线剩余强度分析
焦双健,陈晓磊
(中国海洋大学 工程学院,山东 青岛 266100)
1 铸铁管线强度衰退机理
土壤腐蚀是造成管线抗力衰退的最主要因素。在土壤的腐蚀作用下,埋地管线的管壁变薄,形成体积型缺陷。缺陷部位产生应力集中现象,在同等外部荷载作用下更容易造成管线的损伤。同时,还会使管线的强度不断降低,严重影响管线的使用寿命。
铸铁管线的腐蚀是一个自我抑制的过程,即在腐蚀初期管线的腐蚀速率较大,当腐蚀持续进行时,腐蚀生成物将附着于管壁表面,从而减少管壁与土壤的接触面积,起到保护作用,导致管线腐蚀速率的降低,后期的腐蚀速率随着龄期增加而趋向稳定。目前,管线腐蚀速率的计算模型主要有3种:线性腐蚀模型,二阶段腐蚀模型和幂函数腐蚀模型。
线性模型的形式简单、影响因素少,实际研究的腐蚀规律差别较大,应用并不广泛。二阶模型由Rajan提出,无法准确描述龄期超出试验范围的管线,也不推荐使用。
幂函数模型是由J.R.Rossume提出的,通过模型修正后得到的最终Rossume幂函数腐蚀模型公式为

式中:k0为模型修正系数,k0=0.3223;铸铁中ka=1.4,a=0.22;A为管道暴露在土中的腐蚀面积;n与kn取值与土壤透气性相关,如表1所示;T为管龄;ρsoil为土壤电阻率,代表土壤酸碱度。
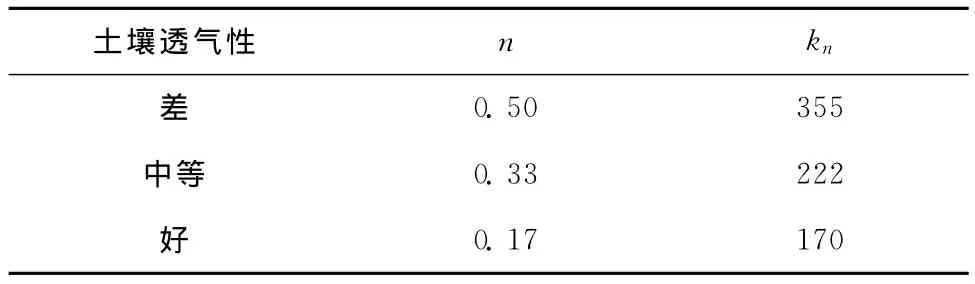
表1 Rossum幂函数模型的土壤腐蚀常数表
通过对幂函数、二阶函数及线性函数模型比较得知,采用幂函数模型对铸铁管线的剩余强度进行评估更可靠。
2 铸铁管线剩余强度计算
腐蚀作用所产生的体积型缺陷包括轴向缺陷和环向缺陷两种,其中轴向缺陷对管线所能承受工作压力的影响较大,环向缺陷对管线受弯极限承载力的影响较大。
2.1 轴向缺陷下的剩余强度计算
本文采用最为普遍实用的ASME B31G.1991评价法来计算管线轴向缺陷下的剩余强度,计算模型为

式中:σp为失效周向应力,MPa;β为管道材料的流变应力,MPa;A0为未受损管线纵向面积,mm2;A为腐蚀缺陷的轴向投影面积,mm2;M为Folias膨胀系数。
σf的取值公式为

式中:σb为某一强度级别管材的拉伸强度;β为拉伸强度变化系数,取1.0。
Folias膨胀系数的表达方式有多种,文中依据最新B31G准则选取式(4)作为膨胀系数表达式

式中:D为管道外径,mm;L为腐蚀缺陷轴向投影长度,mm;t为管道壁厚,mm。
由Folias膨胀系数计算公式可知,腐蚀缺陷越短,膨胀因子数值对计算结果的影响越小。
改革开放四十年来,我们党和国家不断进行着自我完善的实践活动。回顾改革开放的历史进程,没有思想的解放作为前提,没有观念的转变作为契机,就不可能拥有行动上的实际力量推动社会向着既定的目标不断发展。历史经验告诉我们,任何实践都需要在一定的目标取向中去完成,而这种目标取向从根本上来说就是人们对于历史以及未来的自我认知及合理预期。中国改革开放四十年始终坚持着在反思问题与变革现实、增长目标与实现预期有机统一的维度上进行着中国特色社会主义的建设与发展。
对于式(2)中腐蚀缺陷的投影面积A的计算难度较大,为降低计算腐蚀缺陷A的难度,文中将腐蚀缺陷A简化为抛物线进行计算,如图1所示。将该抛物线进行面积积分得

简化后的缺陷面积表达式只与缺陷的长度和缺陷深度有关,因此,轴向缺陷下的铸铁管线剩余强度计算模型可表示为
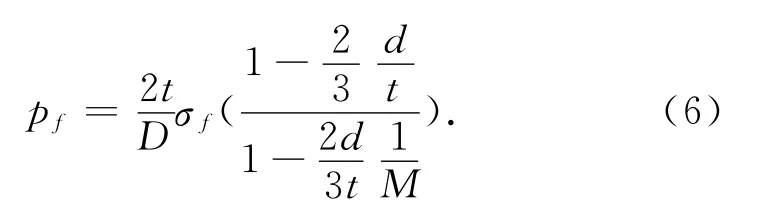

图1 腐蚀缺陷A的抛物线
2.2 环向缺陷下的剩余强度计算
环向缺陷下,管线剩余弯曲极限承载力可通过NSC准则分析进行计算。当管线截面材料开始屈服进入塑性状态,截面应力均达到材料本身所能抵抗的最大应力时,所施加的外荷载即为含环向缺陷管线的塑性极限荷载。
埋地管线受土壤的腐蚀是电化学腐蚀过程,在管线使用期间,由于土壤本身重力作用,管线首先受管顶上部土壤的腐蚀随后沿环向扩展,形成外腐蚀缺陷,本文将腐蚀坑形状假定为沿管线外壁等深的环状缺陷,如图2所示。
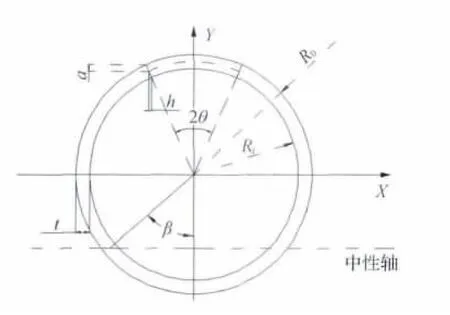
图2 腐蚀坑形状
图中a为缺陷厚度,mm,h为缺陷处的剩余壁厚,mm,Ri为内半径,mm,R0为外半径,mm,t为管壁厚度,mm。
由于管顶上部缺陷的存在以及外部荷载的作用(弯矩,轴向拉伸荷载),管线弯曲中性轴向下偏离了管道截面中心。如果土壤对管线造成的腐蚀缺陷处于管顶上部,可认为此缺陷仅处于受拉或受压应力区(依据弯矩加载方向判定)。假定缺陷处于受拉应力区,此时弯矩方向向下,如图3所示。
本文仅考虑纯弯曲荷载M作用下含环向缺陷管线的极限承载力,拉伸荷载取N=0。由于整个缺陷截面分为拉应力和压应力两个区,因此,在整个截面存在着拉、压两种应力。为保持力的平衡,拉应力及压应力之和与拉伸荷载N的和为0,此时,截面应力为即将达到材料塑性极限的流变应力σf,由此可断定拉、压区间的分界线(弯矩中性轴)。
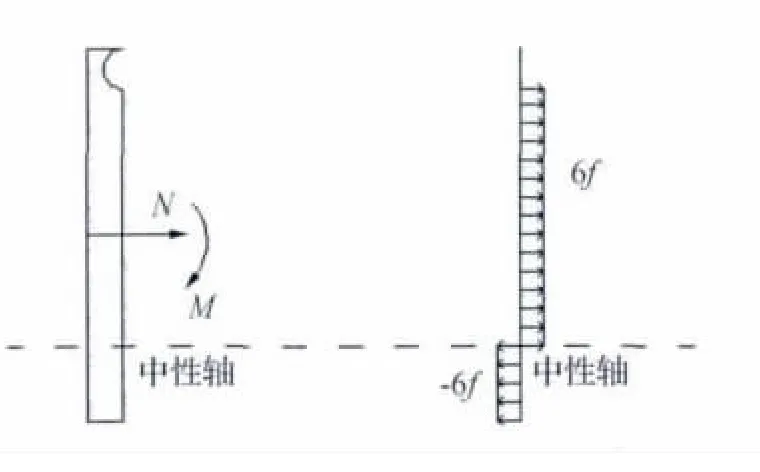
图3 轴向界面受力分析
1)当θ+β<π时

2)当θ+β>π时

在式(7)、式(8)中,M0为无缺陷管线极限弯曲荷载。
3 兖州市城区部分铸铁管线剩余强度计算
本文以兖州市城区部分铸铁埋地管线为例进行剩余强度的计算。该地区共77条管线,48个节点,铸铁管线使用率为70%。供水水源位于城市主干供水网西侧,供水管网如图4所示。

图4 兖州城区供水管网系统
兖州城区的部分管线管径为200mm、300mm、400mm,壁厚为9mm,假定管线的轴向缺陷长度L为管线腐蚀坑深度(d)的100倍,腐蚀坑在轴向投影为二次抛物线。管线的环向缺陷腐蚀坑深度dh等深,缺陷弧长Lh为dh的200倍。土壤pH值为5,管线轴向暴露在土中,腐蚀长度为25mm,透气性分为好、中、差三类,土壤的电阻率取值分别为410omb-cm、1300omb-cm、7380omb-cm 的情况下,运用公式(1)计算出管线的腐蚀坑深度,运用公式(6)计算轴向缺陷管线的强度比,运用公式(7)、(8)计算环向缺陷管线的极限承载比,从而得出不同条件下的管线腐蚀坑深度及强度比。
3.1 轴向缺陷下极限承载力的计算
在土壤透气性较好、电阻率为1300omb情况下,不同管径的管线腐蚀坑深度随龄期变化,如图5所示,强度比随龄期变化,如图6所示。

由图5和图6可以看出,管线的腐蚀坑深度随管龄的增加而变大,其中,在管龄一定的情况下,管径越粗腐蚀坑深度变化越大。而管线的剩余强度与原强度之比随管龄的增加而变小,其中管径粗的管线剩余强度与原强度之比较管径细的管线要小。
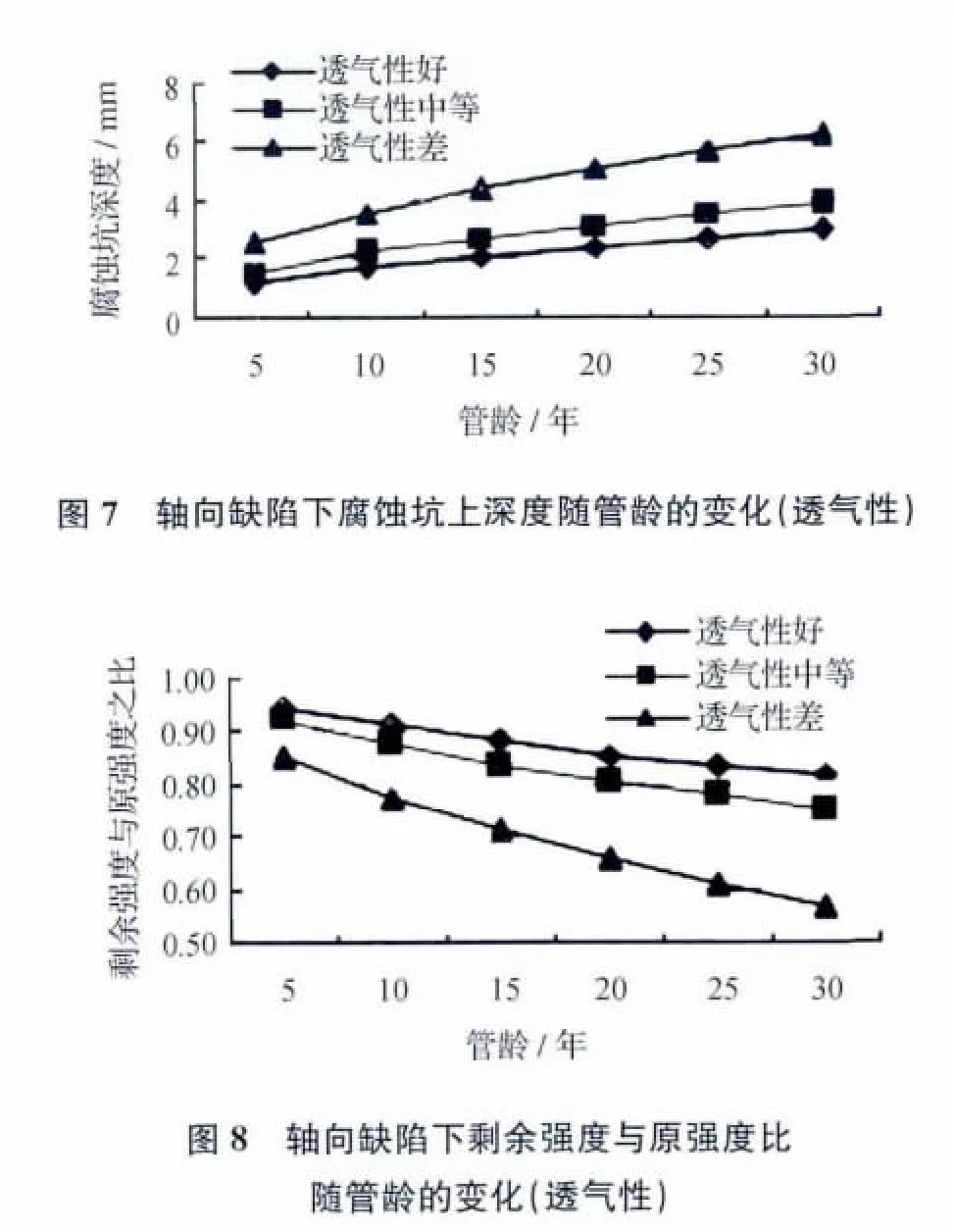
同理,可以求解出当管径为400mm、电阻率为1300omb情况下的腐蚀坑深度、强度比随时间和透气性的变化数据。计算结果如图7、图8所示。
由图7和图8可以看出腐蚀坑深度的变化也受土壤透气性的影响,透气性越差的管线腐蚀坑深度越大,透气性好的管线腐蚀坑深度也相对较浅。管线的剩余强度与原强度之比同样受透气性的影响,透气性差的管线剩余强度与原强度之比较透气性好的管线要小一些。
土壤透气性较差、管径为400mm的管材,其腐蚀坑深度和强度比与土壤电阻率和管龄的关系如图9、图10所示。

从图9和图10可以看出,土壤电阻率的大小对腐蚀坑的深度具有重要影响,电阻率越小,腐蚀坑深度就越大,电阻率越大,腐蚀坑深度越小。同样,电阻率的变化对剩余强度与原强度之比也有重要影响,土壤电阻率小的比电阻率大的剩余强度之比要小一些。从计算结果还可得知,在电阻率小及透气性差的情况下。铸铁管线腐蚀最为严重,当电阻率为410,龄期大于20年时管壁出现穿孔现象,强度为0。
3.2 环向缺陷极限承载力实例计算
当管线腐蚀所产生的缺陷为环向缺陷时,腐蚀坑深度与环向腐蚀长度比为1∶200,其余条件与轴向腐蚀缺陷相同,计算方法同轴向缺陷。当电阻率为1300omb,透气性好,以管径为变量。管线腐蚀坑深度即所能承受的极限承载力计算如图11、图12所示。

由图11和图12可以看出,在环向缺陷下,腐蚀坑的深度随管龄的增加而增加,管径大的管线腐蚀坑深度较管径大的管线要深一些。管线的剩余强度与原强度之比随管龄的增加而变小。但是电阻率为1300omb-cm,管径在200~400mm范围内变化,管线强度的衰减受管径影响较小。因为管径增大,腐蚀坑度加深,但管径大,环形面积也同样增大。
管径为400mm,土壤电阻率同为1300omb的情况下,管线腐蚀坑深度和剩余强度比与土壤透气性和管龄间的关系如图13、图14所示。

由图13和图14发现,在环向缺陷下,透气性对腐蚀坑深度的影响比较明显,透气性好的管材腐蚀坑深度明显较小,而透气性差的管材腐蚀坑深度则较大。透气性的好坏对剩余强度与原强度之比也具有重要影响,其中透气性好的管材强度之比要大一些。
管径为400mm,土壤透气性较差以电阻率为变量的情况下,管线腐蚀坑深度和剩余强度比与土壤透气性和管龄间的关系如图15、图16所示。

图15 环向缺陷下腐蚀坑深度随管龄的变化(电阻率)
由图15和图16可以看出,环向缺陷下的电阻率越小,腐蚀坑深度越深,剩余强度与原强度之比越小。当透气性差,电阻率小腐蚀程度越重,与轴向缺陷规律相同。
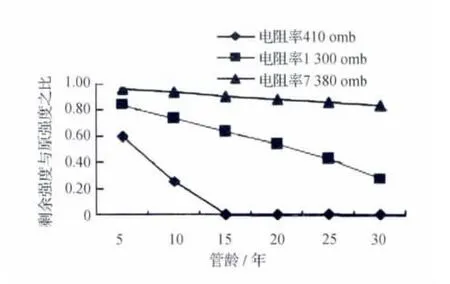
图16 环向缺陷下剩余强度与原强度之比随管龄的变化(电阻率)
4 结束语
铸铁管线的剩余强度计算是在综合分析管线强度衰退机理的基础上进行的。腐蚀作用导致的管线缺陷通常包括轴向缺陷和环向缺陷两种,轴向缺陷下的管线剩余强度可采用ASME B31G.1991评价法,环向缺陷下的剩余强度可通过结构塑性分析进行计算。管线剩余强度计算模型的构建对于保证管网的正常运行、保证管网的经济有效管理具有重要作用。
[1] S TESFAMARIAM,B RAJAN.Impact of uncertainties on the translation of remaining pipe wall thickness to structural capacity [J].INFRA 2004Urban Infrastructure:Managing the Assets,Mastering the Technology,2005:1-16
[2] J R ROSSUM.Predietion of pitting rates in femurs metals from soil Parameters[J].Journal(American Water Works Association),1969,61(6):305-310
[3] 侯忠良.埋地管线抗震[M].北京:学术书刊出版社,1990.
[4] 陈严飞,李昕.不规则腐蚀缺陷管道极限承载力研究[J].工程力学,2009,26(11):190-195
[5] 王大伟.城市给水管管壁强度可靠性研究[D].杭州:浙江大学,2003
[6] 冯贤桂.天然气管道的疲劳可靠寿命计算[J].重庆大学学报,2002,25(7):133-136

