具有奇异系数拟线性抛物型不等式中解的Liouville定理*
方钟波,孙 璐
(中国海洋大学数学科学学院,山东 青岛266100)
1 引言及主要结果
本文考虑带奇异系数拟线性抛物型不等式柯西问题

非负非平凡整体弱解在某些带参数的函数空间中的非存在性,其中加权函数a(x,

上述双重退化抛物型不等式(1)出现于流体力学、人口动力学及生物群体力学等诸多领域中[1-2]。从流体力学角度来说,描述多孔体介质中非牛顿渗流现象,可描述气体或液体在多孔体介质中的流动,其中a(x,t)up为正时叫“热源”项,负时叫“冷源”项。
Fujita[3]研究半线性抛物型方程ut=Δu+up柯西问题的整体解的非存在性时提出了临界指数pc=1+(称为Fujita临界指数),并受到许多学者的高度重视。非线性偏微分方程整体解的不存在性是一类非线性Liouville定理,可以用它证明有界域上的解的某些性质,还是爆破理论或奇点理论的一种本质体现[4]。
近年来,圆锥区域及整体空间上带变系数或不带变系数的椭圆型方程、不等式(组)的Liouville型定理及整体解的非存在性方面有许多结论,见[5-10]等相关文献。比如,文献[5]中,Gidas and Spruck(在无穷远处没有任何条件的情况下)证明了次临界椭圆型方程解的Liouville定理(不存在非平凡C2解)且用它得到了先验估计。
最近,抛物型方程或不等式(组)中Liouville定理的研究也引起了许多学者的兴趣。方程(1)中,当σ=0,m=0且加权函数为a(x,t)≥ (|x|2+t)-γ时魏公明等[11]利用试验函数法得到了非负非平凡整体弱解的非存在性结论。Fang Z B等[12]利用试验函数法得到了变系数慢扩散不等式柯西问题

在圆锥区域中的非线性Liouville型定理。其它关于带加权函数的慢扩散方程柯西问题中解的非存在性结论方面参考了文献[13]。
由此启发,本文研究带变系数和加权函数的拟线性抛物型不等式(1)的非负非平凡整体弱解在带参数的函数空间中的非线性Liouville定理。目的在于找到变系数指数与加权函数的指数对非负非平凡整体弱解的非存在性影响,且具有无穷远处无任何条件、对初始值没有作任何正则性假设(导致初值在超平面t=0上可能没有很好的‘迹’)、不用比较原理和极值原理等特点。通过适当构造试验函数来建立Universal估计值(不依赖于初始值),从而得出在适当的临界指数范围内非负非平凡整体弱解非存在性结论。详细结论如下:定理1(Liouville定理)成立,且



在(18)式两端令R→∞就得到
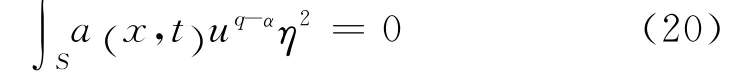
因为η是任意的,所以在S上几乎处处成立u=0。
[1] Bebernes J,Eberly D.Mathematical Problems from Combustion Theory[M].New York:Springer-Verlag,1989.
[2] Wu Z,Zhao J,Yin J.Nonlinear Diffusion Equations[M].Singapore:World Scientific,2001.
[3] Fujita H.On the blowing up of solutions to the Cauchy problem for ut=Δu+u1+α[J].J Fac Sci Univ Tokyo Sect 1AMath,1966,13:119-124.
[4] Galaktionov V A,Vazquaez J L.Continuation of blowup solutions of nonlinear heat equations in several space dimensions [J].Comm on Pure and Appl Mat,1997,50(1):1-67.
[5] Gidas B,Spruck J.Global and local behavior of positive solutions of nonlinear elliptic equations[J].Comm on Pure and Appl Mat,1981,24:525-598.
[6] Gidas B,Spruck J.A priori bounds for positive solutions of nonlinear elliptic equations[J].Comm in P D E,1981,6(8):883-901.
[7] Kondrat’ev V A.Boundary value problems for elliptic equations in domains with conic and angular points[J].Trans Moscow Math.Soc,1967,16:209-292.
[8] Hayakawa K.On nonexistence of global solution of some semilinear parabolic differential equations[J].Proc Japan Acad Ser A,1979,49:503-505.
[9] Mitidieri E,Pohozaev S L.A priori estimates and blow-up of solutions to non-linear partial differential equations and inequalities[J].Proc Steklov Inst Math,2001,234:3-383.
[10] Laptev G G.The absence of global positive solutions of systems of semilinear elliptic inequalities in cones[J].Izv Math,2000,64(6):1197-1215.
[11] 魏公明.具奇系数发展型p-laplace不等方程整体解的不存在性[J].数学年刊 A辑,2007,28A(2):387-394.
[12] Fang ZhongBo,Fu Chao,Zhang LinJie.Liouville theorems of slow diffusion differential inequalities with variable coefficients in cone[J].J.of KSAIM,2011,15(1):43-55.
[13] Lian Songzhe,Liu Changchun.On the existence and nonexistence of global solutions for the porous medium equation with strongly nonlinear sources in a cone[J].Arch Math,2010,94:245-253.
[14] Kartsatos A G,Kurta V V.On a comparison principle and the critical Fujita exponents for solutions of semilinear parabolic inequalities[J].J London Math Soc,2002,66(2):351-360.

