基于柔度矩阵的斜拉桥拉索损伤识别研究*
董晓马,岳鹏威
(郑州航空工业管理学院土木建筑工程学院,河南 郑州450015)
由于外型美观、施工方便和造价经济,斜拉桥目前已经成为大跨度桥梁的主要桥型之一,而斜拉索是斜拉桥的主要的受力构件,其安全性和耐久性对桥梁的正常使用及整体安全是极为重要的,一旦拉索中产生了损伤导致其承载能力降低或丧失,从而致使桥梁垮塌事故,就不可避免的造成重大人员伤亡、巨大的经济财产损失和恶劣的社会影响(如广州海印大桥断索等)。而近年来,桥梁结构健康监测技术的发展为桥梁的安全保障另辟蹊径[1-4],可以彻底克服人工检测的滞后性和低效性,其方法主要是通过布置在桥梁结构上的传感器,对桥梁工作状况进行长期的在线监测,并利用监测信息反演结构的状态,以尽早识别桥梁损伤并及时采取必要的措施地避免桥梁产生破坏。
目前就如何识别斜拉桥拉索损伤已引起桥梁工程界的高度关注,许多学者对此进行了广泛研究[5-8],并初步取得一些有益的成果,但这些成果多局限于数值算例且没有考虑噪声的影响。针对在实际测试时由于测试误差的影响,往往只能较准确地获得前几阶模态参数,而结构高阶模态难以准确获取的特点;考虑到柔度矩阵与自振频率的平方成反比,当模态频率较大时其对应模态参数对柔度矩阵贡献可忽略不计,采用前几个低阶模态参数计算就能获得精度较好的柔度矩阵。本文以润扬大桥为背景,以实桥模型桥为试验对象,提出利用柔度差矩阵指标来对斜拉桥拉索损伤进行识别。研究结果表明,本文方法能有效的对模型斜拉桥拉索损伤给予准确的识别。
1 柔度矩阵损伤识别机理
由模态分析理论可知特征方程有,


式中:K、M分别是结构整体刚度矩阵和质量矩阵;Φ是正则振型矩阵;Λ是模态频率矩阵。
由式(2)可知

将式(1)两端右乘式(3)两端,有

式中ωi、Φi分别为第i阶模态频率和正则特征矢量。将式(1)两端左乘柔度矩阵F,右乘Λ-1有

将上式两端右乘式(3)两端有

由上式可知柔度矩阵有
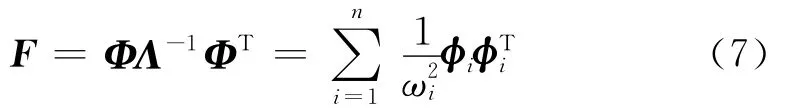
由式(7)可以看出,模态参数对柔度矩阵的贡献与自振频率的平方成反比,随频率增大,高频项的影响可以忽略不计,所以只需测量前s个低阶模态参数就能获得精度较好的柔度矩阵。而实测时,由于测试误差的影响,往往只能较准确地获得前几阶模态参数。因此,利用柔度法进行结构损伤识别,在获得相同的试验模态参数条件下比采用刚度法更为精确[9]。
根据式(7)有损伤结构柔度矩阵为
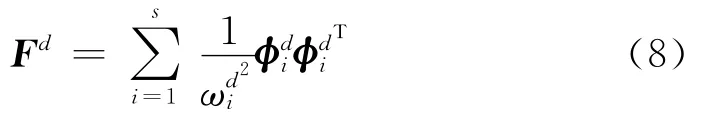
则结构损伤前后模态计算结构柔度差矩阵为

柔度差矩阵ΔF的第j列与自由度j对应,其Δfij元素代表j自由度在单位力作用下第i自由度的静态位移的改变量。在结构损伤点附近,柔度差值相对来说将有较大的改变,故可根据柔度差矩阵可确定损伤位置。若结构在第i点有损伤,则Δfii将产生更大的变化,对损伤更加敏感[10]。所以本文采用柔度差矩阵对角元素相对量来作为损伤位置敏感指标,即
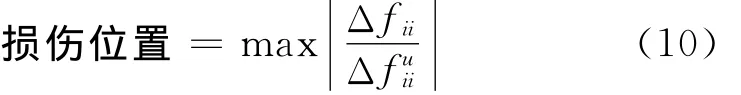
2 模型斜拉桥拉索损伤模拟及识别
根据相似理论对润扬大桥建立了模型桥,试验模型长12 640mm,主跨长6 780mm,边跨长2 930mm,桥面宽565mm,索塔高2 450mm,如图1所示。斜拉索的采用直径1.0mm的高强度钢丝模拟,为能够调整索的应力,各个拉索与主梁采用微调螺丝进行联接,通过调整其长度,可改变斜拉索的张紧程度,如图2所示。模型桥索塔采用铝合金箱形截面,截面面积4 920mm2,弹 性 模 量 0.7×105N/mm2,抗 弯 惯 矩7.98×106mm4。并采用铜块来进行配重,以满足桥塔顺桥向和横桥向2个方向的抗弯刚度和抗扭刚度,索塔模型见图3。
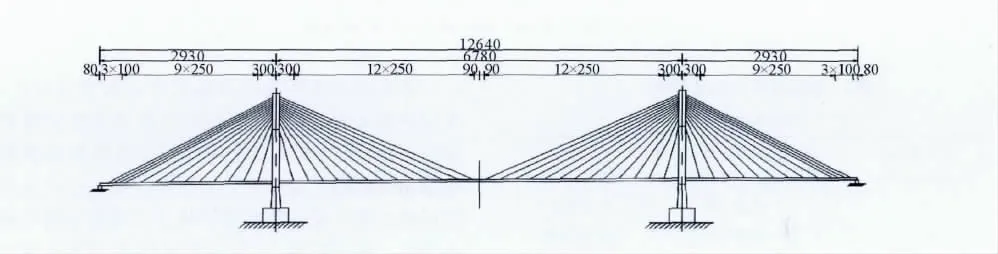
图1 模型斜拉桥尺寸Fig.1 Model cable-stayed bridge size

振动试验系统是由信号发生器、激振器、加速度传感器、数据采集仪、计算机处理系统、模型斜拉桥等组成。在斜拉桥桥面主跨1/4位置布置激振器,在模型斜拉桥桥面两侧斜拉索与主梁连接位置、主梁跨中及主梁支座位置分别布置加速度传感器,用以采集模型桥竖向振动的加速度响应,加速度传感器的桥面安装如图2所示,布置测点位置如图5所示,共27个测点,从左至右依次为测点1、测点2……。试验时利用计算机控制激振器进行随机噪声激励与峰值识别法进行模型斜拉桥的动力特性试验,图4是试验测得的模型桥前四阶振型及其频率。

图4 模型桥前四阶振型及其频率Fig.4 First four vibration modes and frequencies of model bridge
试验对斜拉索的损伤进行了模拟,模拟拉索完全失效情况。考虑到模型斜拉桥的斜拉索是以桥面横向中心线为对称轴对称布置的,所以本文仅讨论桥面横向中心线左侧的拉索损伤的情况。试验测点位置、斜拉索编号分别如图5所示。损伤试验的损伤工况如表1所示为4种损伤工况、前两为单索A6和J8的损伤,后两工况为双索J8和A6损伤工况、以及J5和A5损伤工况。

图5 试验激励与测点布置示意图Fig.5 Actuator and sensors layout schematic
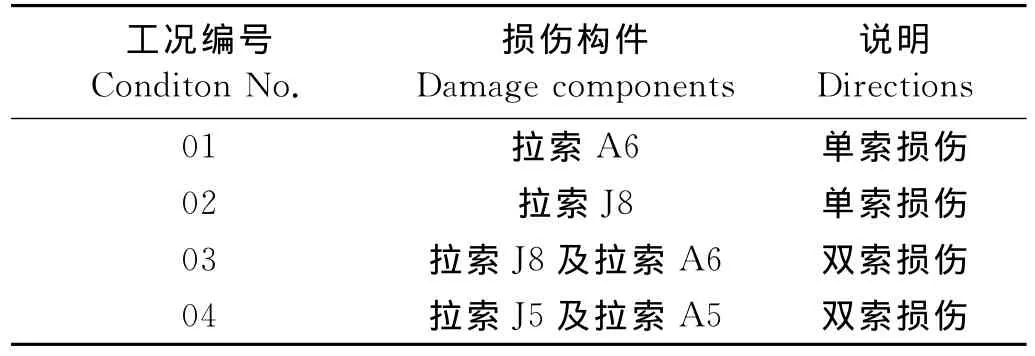
表1 斜拉索损伤工况列表Table 1 Damage conditions
考虑到柔度矩阵与自振频率的平方成反比,当模态频率较大时,其所对应模态参数对柔度矩阵贡献可忽略不计,所以本文只采用前两个低阶模态参数计算模型斜拉桥的柔度矩阵。根据前述相关公式及实测模型桥梁的模态频率和振型计算各工况模型斜拉桥柔度差矩阵。限于篇幅,本文这里只给出工况1柔度差矩阵,如表2所示。

表2 工况1柔度差矩阵Table 2 The flexibility difference matrix of case 1
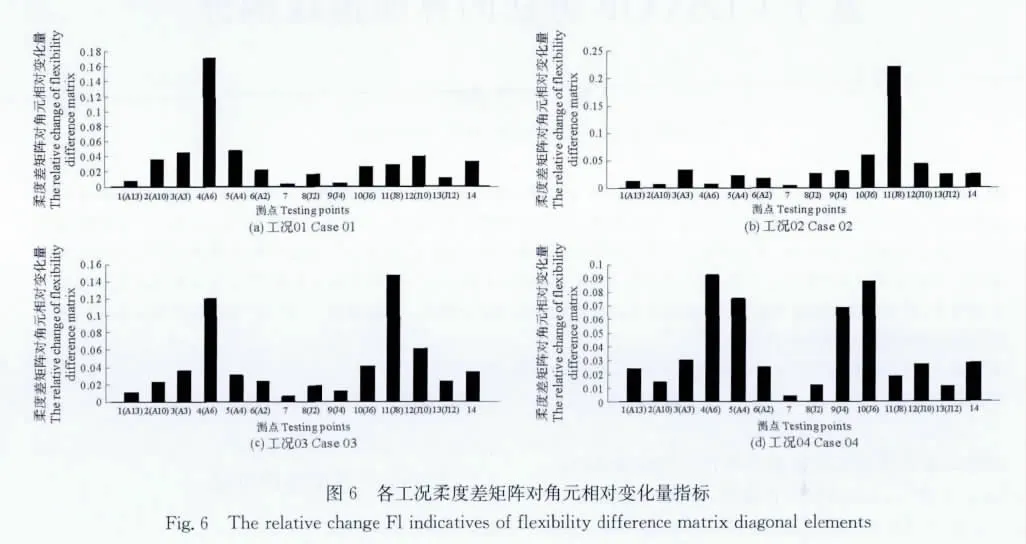
各工况矩阵对角元素相对量损伤位置敏感指标如图6所示。由图可见,对于单拉索损伤工况01、02,图中曲线峰值能够准确的指示出斜拉桥拉索A6和J8损伤位置;对于双索损伤工况03,由图中曲线峰值能同时准确地识别出斜拉桥拉索A6和J8损伤位置;而在双索损伤工况04中,图中曲线峰值未能明确给出拉索J5和A5损伤位置,究其原因与在损伤拉索J5和A5处未布置加速度传感器有关,尽管如此,工况04检测结果仍有效地给出局部损伤位置范围,此范围包含有拉索J5和A5损伤位置,这为进一步检测与确认提供了极大的方便。另外在实际的大跨度斜拉桥中,多个位置斜拉索同时出现较大程度的损伤的情况并不多见,对于多位置损伤识别可视为连续单位置损伤识别来处理。
3 结语
斜拉索作为大跨斜拉桥的主要承重构件,其安全性和耐久性对桥梁的正常使用和整体安全是非常重要的,所以及早识别拉索损伤并及时采取必要的措施地避免斜拉桥产生破坏是非常必要的。因此,本文在分析柔度矩阵损伤识别机理基础上,提出基于柔度差矩阵斜拉桥拉索损伤识别的方法,并通过模型斜拉桥为试验对象研究该法的适用性。试验研究结果表明,柔度差矩阵指标是拉索损伤很好的敏感标识量,对单位置拉索损伤能够准确的给予识别,对于多位置拉索损伤识别,指标也能给予较好识别效果。因此,利用柔度差矩阵指标可有效的识别出斜拉桥拉索损伤位置。
[1] Chan T H T,Li Z X,Ko J M.Evaluation of typhoon induced fatigue damage using health monitoring data for the Tsing Ma Bridge[J].Structural Engineering And Mechanic,2004,27:655-670.
[2] Chang P C,Flatau A,Liu S C.Review Paper:Health monitoring of civil infrastructure[J].Structural Health Monitoring,2003,2(3):257-267.
[3] Aktan A E,Helmicki A J,Hunt V J.Issues in health monitoring for intelligent infrastructure[J].Smart Materials and Structures,1998,7:674-692.
[4] 裴强,郭迅,张敏政.桥梁健康监测及诊断研究综述[J].地震工程与工程振动,2003,23(2):61-67.
[5] 杨杰,李爱群,缪长青.BP神经网络在大跨斜拉桥的斜拉索损伤识别中的应用[J].土木工程学报,2006,39(5):72-77.
[6] 赵玲,李爱群,缪长青,等.大跨斜拉桥的拉索损伤识别[J].桥梁建设,2004(5):19-22.
[7] 孙宗光,倪一清,高赞明,等.基于斜拉索振动测量与神经网络技术的斜拉桥损伤位置识别方法[J].工程力学,2003,20(3):26-30.
[8] 杨少军.桥梁拉索体系损伤的检测和监测方法[J].公路交通技术,2005(3):130-134.
[9] Zhao J,Dewolf J T.Sensitivity study for vibrational parameters used in damage detection[J].Journal of Structural Engineering,1999,125(4):410-416.
[10] Pandey A K,Biswas M.Damage detection in structures using changes in flexibility[J].Journal of Soundand Vibrtion,1994,169(1):3-17.

